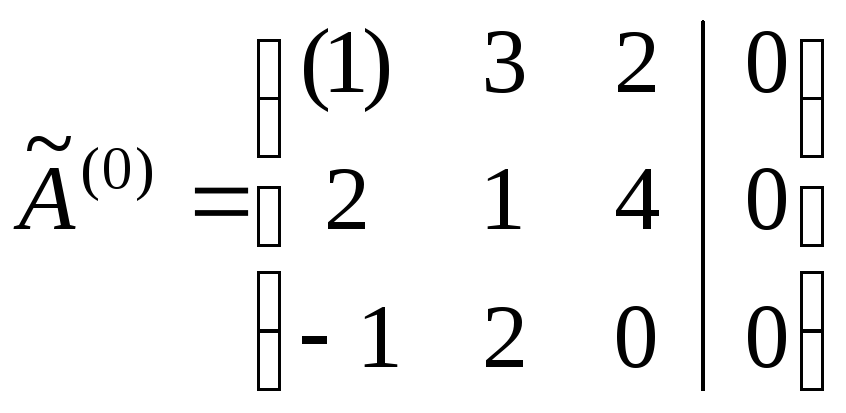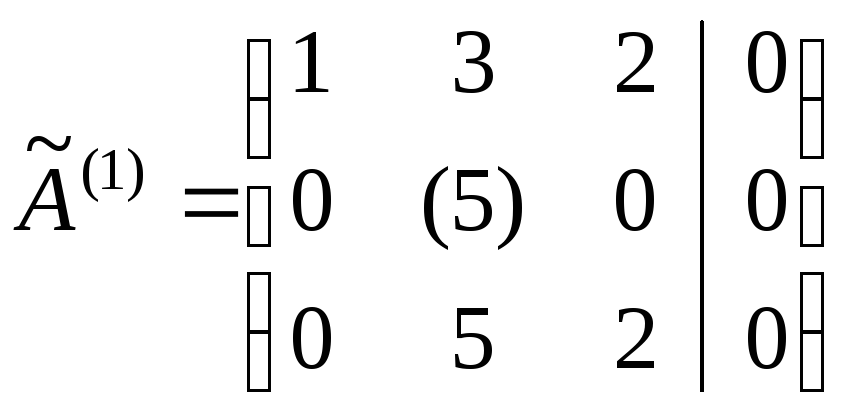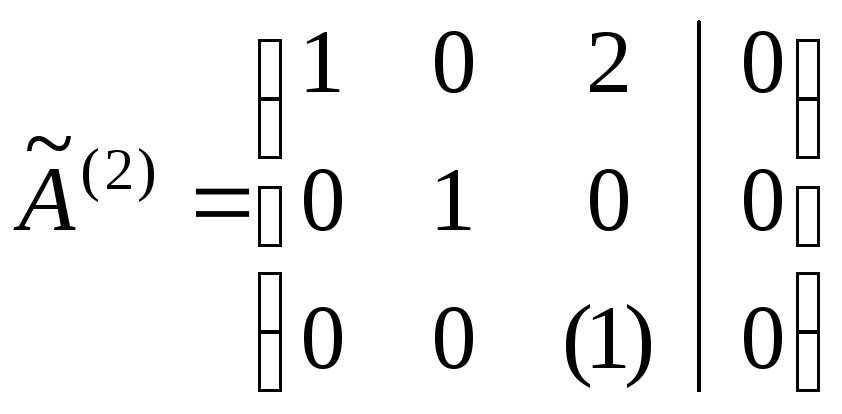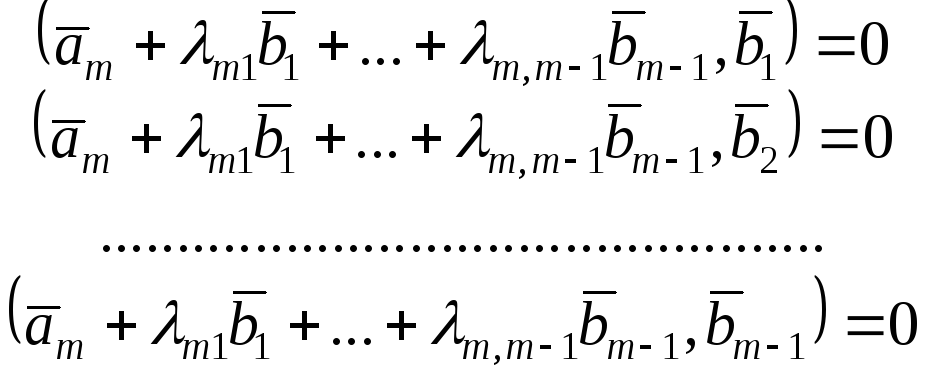5.4. Изоморфизм векторных пространств

Определение.Векторные пространстваRиR’ называются изоморфными, если между их векторами-элементами можно установить взаимно однозначное соответствие такое, что еслии, где,, тои.

Из определения изоморфизма следует, что если ,... – векторы изR,a,... – вектора изR', то равенстворавносильно равенству. Следовательно, линейно независимым векторам изRсоответствуют линейно независимые векторы изR'и обратно.

Пространства различной размерности не могут быть между собой изоморфны. В самом деле, пусть RиR'изоморфны. Тогда максимальное число линейно независимых векторов вRиR'одно и то же, т.е. размерности пространствRиR'равны.

Все пространства, имеющие одну и ту же размерность n, изоморфны между собой.

5.5. Преобразование координат при изменении базиса

Пусть и– два базиса пространстваR_n. Каждый векторможно выразить через векторы:

, ……………………………

(5.5.1)

Выражения (5.5.1) показывают, что новые базисные векторы получаются из старых базисных векторовс помощью матрицы:

,

причем коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрица.

Матрица Аназывается матрицей перехода от базисак базису.

Определитель матрицы Аотличен от нуля, так как в противном случае ее столбцы, а следовательно, и векторыбыли бы линейно зависимы.

Рассмотрим, как связаны между собой координаты одного и того же вектора в старом и новом базисах. Пусть

(5.5.2)

и в то же время

(5.5.3)

Подставим в (5.5.3) вместо их выражения из (5.5.1):

(5.5.4)

Из (5.5.2) и (5.5.4) в силу единственности разложения вектора по базисуполучаем

,

или в матричном виде

X=AX',

(5.5.5)

где ,.

Уравнение (5.5.5.) показывает связь между координатами х_jиx'_jвекторав базиcахи,.

Из (5.5.5.) получаем:

X'=А^-1Х

Таким образом, при переходе от базиса к базисукоординаты векторапреобразуются с помощью матрицыА^-1, являющейся обратной к транспонированной матрице, задающей преобразование базисов.

Пример.В базисе,,пространстваR₃заданы векторы,,,. Показать, что векторыобразует базис. Найти координаты векторав базисе. Выразить связь между базисамии.

Решение.Векторыобразуют базис пространстваR₃, если они линейно независимы. Векторылинейно независимы если векторное равенствовыполняется тогда и только тогда, когда,,. Найдем решение векторного равенства

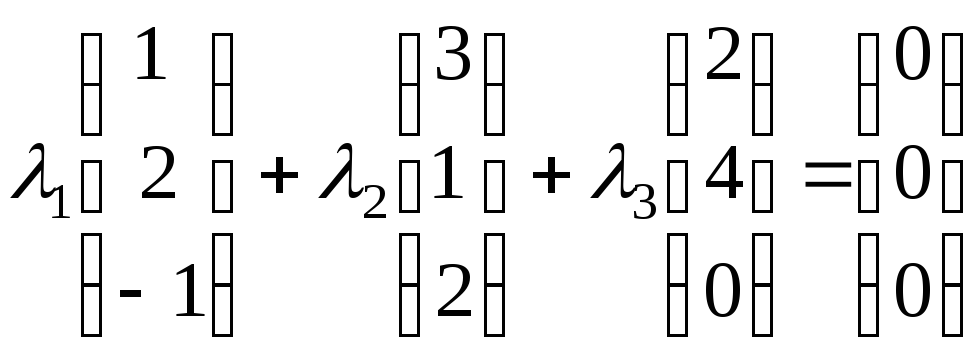
методом Жордана-Гаусса.

откуда .

Система векторов линейно независима и, следовательно, образует базис в R₃.

Выразим каждый вектор через векторы:

Матрица Аперехода от базисак базисуимеет вид:

.

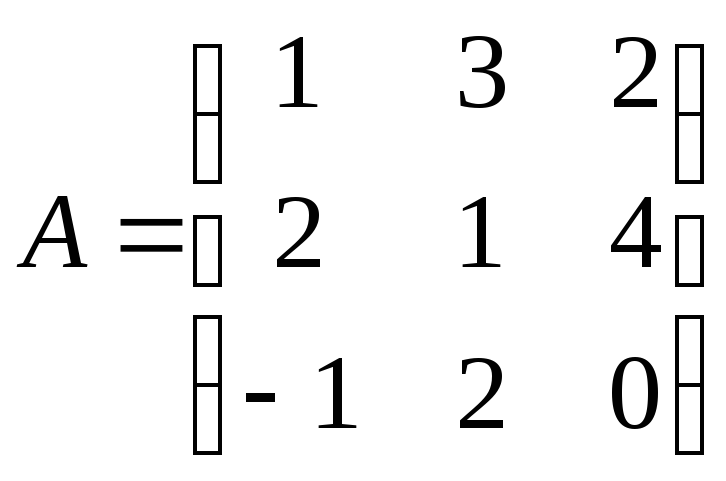Вычислив

,

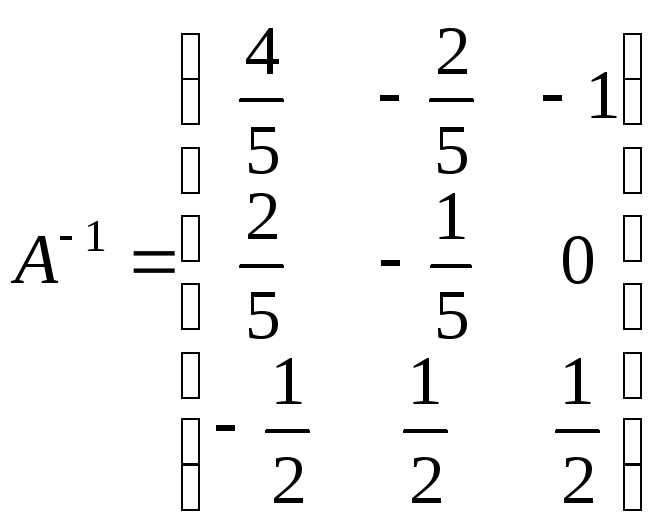определим координаты векторав новом базисе

.

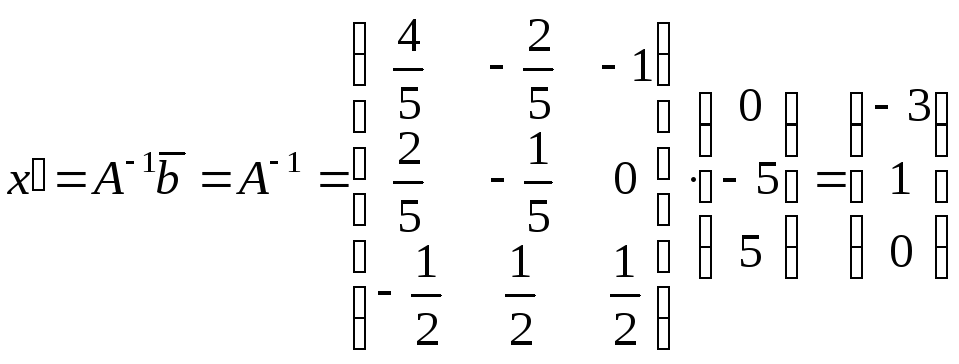Таким образом, в базисе векторопределяется координатами.

Связь между базисом и базисомопределяется из следующих соотношений:

,

,

,

или в матричном виде:

E=XA,

где

.

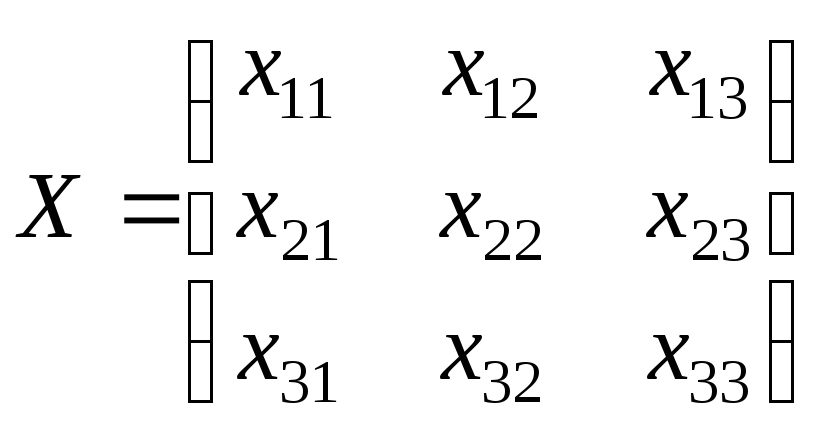Решение данного матричного уравнения имеет вид X=A^-1, откуда получаем

,

,

,

Данные соотношения выражают связь между базисами.

5.6. Евклидово пространство

n-мерное векторное пространство Е_n называется евклидовым, если каждой паре векторов иизЕ поставлено в соответствие вещественное число (,), называемое скалярным произведением, при чем это соответствие удовлетворяет следующим аксиомам:

I. Линейности по первому аргументу

;

II. Симметрии

;

III. Положительной определенности

, при

и тогда и только тогда, когда.

Из линейности по первому аргументу и симметрии следует и линейность по второму аргументу

Примеры.

1. Векторами пространства E_nявляется любая упорядоченная системаnдействительных чисел. Сложение векторов и умножение их на число определены в п.5.1, а скалярное произведение векторовиопределим формулой.

Легко убедиться в том, что аксиомы I-III действительно выполняются.

2. Рассмотрим более общий случай. Вектор по-прежнему определим как упорядоченную совокупностьnдействительных чисел. Сложение векторов и умножение их на число определим так же, как в примере 1.

Зададимся некоторой квадратной матрицей А=(a_ij)_n,n, Скалярное произведение векторовиопределим формулой

(5.6.1)

Рассмотрим, каким условиям должна удовлетворять матрица А, чтобы определенное данной формулой скалярное произведение удовлетворяло бы аксиомамI-Ш.

Непосредственной проверкой можно убедиться в том, что аксиома I выполняется для любой матрицы А=(a_ij)_n,n. Для того, чтобы была выполнена аксиома II, т.е. чтобы выражениебыло симметричным относительнои, необходимо и достаточно, чтобы, т.е. чтобы матрицаА=(a_ij)_n,n, была симметричной.

Аксиома IIIтребует, чтобы выражение

(5.6.2)

было неотрицательно для любых и обращалось в нуль лишь если.

Однородный многочлен (квадратичная форма), определяемый формулой (5.6.2), называется положительно определенным, если он принимает неотрицательные значения и обращается в нуль, только тогда, когда все равны нулю. Следовательно, аксиомаIIIтребует, чтобы квадратичная форма (5.6.2) была положительно определенной. Таким образом, всякая матрицаА=(a_ij)_n,nзадает скалярное произведение вЕ_n, определяемое формулой (5.6.1), если только эта матрица симметричная и соответствующая ей квадратичная форма положительно определенная.

Если а качестве матрицы А=(a_ij)_n,nвзять единичную матрицуЕ, т.е. положитьa_ii=1, аa_ij=0 (), то скалярное произведение принимает вид

и мы получаем евклидово пространство, определенное в примере 1.

3. Векторами пространства Е_nбудем называть непрерывные функции, заданные на интервале (а,b). Скалярное произведение таких функций определим как интеграл их произведения

.

Можно проверить, что при таком определении скалярного произведения аксиомы I-IIIвыполнены.

С помощью введенного понятия скалярного произведения определим длину вектора и угол между векторами.

Определение.Нормой (длиной)векторавЕ_nназывается корень квадратный из этого скалярного произведения:

.

Векторы и, скалярное произведениекоторых равно нулю, называются ортогональными.

В любом евклидовом пространстве Е_nверна «теорема Пифагора»: еслииортогональны, то

.

Определение.Угол между ненулевыми векторамииопределяется равенством

.

Можно доказать, что в любом пространстве Е_nсправедливо неравенство Коши-Буняковского:

,

откуда следует, что

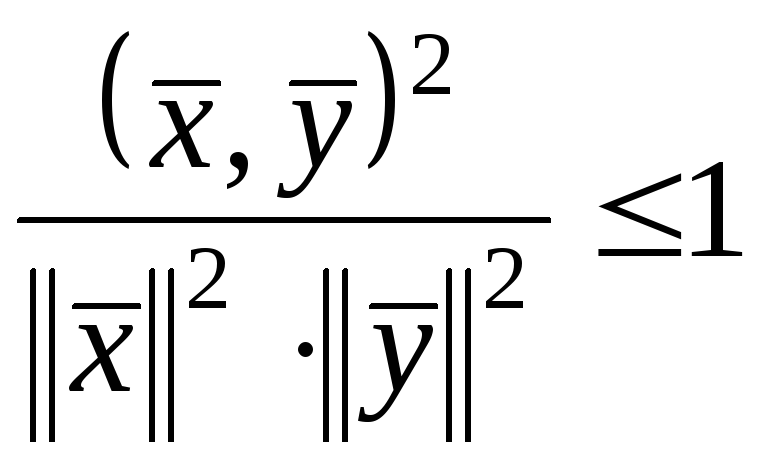
или, что то же самое,

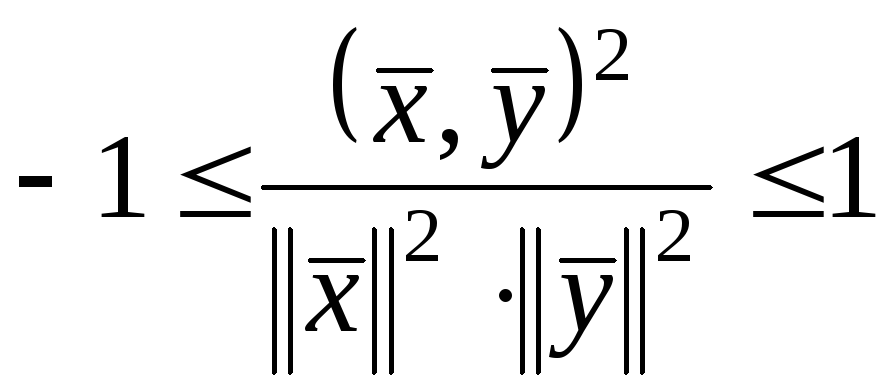
Это означает, что косинус угла между векторами из Е_nпо модулю, не превосходит единицы. Еслии– ненулевые векторы изЕ_n,то ортогональность означает, что уголмежду ними равен. Ненулевой векторпространстваЕ_n, называется нормированным если его норма равна единице. Любой ненулевой вектор можно умножить на некоторое число так, что в результате получится нормированный вектор. Действительно, пусть– ненулевой вектор. Тогдаи достаточно взятьтаким, чтобы

Число называется нормирующим множителем для вектора.

Определение.Система векторовпространстваЕ_nназывается ортогональной, если векторы этой системы попарно ортогональны.

Система векторов называется ортонормированной, если векторы этой системы попарно ортогональны и имеют норму, равную единице, т.е. если

.

Теорема.Ортогональная система ненулевых векторов пространстваЕ_nлинейно независима.

Доказательство.Пусть ненулевые векторыпопарно ортогональны. Тогда.

Покажем, что векторное равенство

(5.6.3)

выполняется тогда и только тогда, когда . Умножим обе части равенства (5.6.3) скалярно на. Получим

из условия ортогональности векторов имеем

,,.

Следовательно, . Аналогично, умножая (5.6.3) на, получим чтои т.д. Таким образом, мы доказали, чтолинейно независимы.

Рассмотрим процесс ортогонализации векторов. Он состоит в том, что из заданных линейно независимых векторов строятсяmпопарно ортогональных векторов. Положим. Векторбудем искать в виде. Числоследует подобрать так, чтобы векторыибыли ортогональны, т.е., откуда.

Допустим теперь, что попарно ортогональные и отличные от нуля векторы уже построены. Векторищем в виде:

,

т.е. вектор мы получаем из вектора«исправлением» его с помощью линейной комбинации уже построенных векторов. Коэффициентынаходим из условия ортогональности векторак векторам:

(5.6.4)

Так как векторы попарно ортогональны, то из равенств (5.6.4) получаем

,

,

……………………………

,

откуда

.

Докажем теперь, что построенный вектор отличен от нуля. Векторесть линейная комбинация векторов. Но векторможно заменить линейной комбинацией вектораи векторови т.д. Окончательно мы получаем, что векторзаписывается в виде

(5.6.5)

откуда следует, что . Действительно, в противном случае левая часть равенства (5.6.5) была бы равна, что противоречит линейной независимости векторов(коэффициент приравен единице). Таким образом, доказано, что. По векторамипостроен вектор. Таким же образом, по векторам, можно построить вектор. Продолжая этот процесс, можно по заданной системеnлинейно независимых векторов вЕ_nпостроить системуnненулевых ортогональных векторов. Докажем следующую теорему.

Теорема.Во всяком евклидовом пространствеЕ_nсуществуют ортонормированные базисы.

Доказательство.По определениюn-мерного векторного пространства в нем существует некоторый базис. С помощью процесса ортогонализации из него можно построить ортогональный базис. Если теперь каждый векторразделить на его норму, то получится ортонормированный базис, образованный векторами

.

Найдем выражение скалярного произведения в координатах. Пусть произвольный базис пространстваЕ_nи

,

.

Тогда

.

Если – нормированный базис, то,а, значит. И обратно, если в базисескалярное произведение векторовиравно, то этот базис ортонормированный, так как в этом случаеи. Если в некотором базисе скалярное произведение, то этот базис ортонормированный.

Пусть – ортонормированный базис вЕ_nи. Умножив обе части последнего равенства скалярно наполучим, т.е.i-я координата векторав ортонормированном базисе равна скалярному произведениюна единичный вектор. Это скалярное произведение называется ортогональной проекцией векторана вектор. Таким образом, координаты вектора в ортонормированном базисе – это его проекции на базисные векторы.

Определим в пространстве Е_nрасстояние между векторами. Расстояниемежду векторамииопределяется как норма вектора:

.

Из определения расстояния следует, что

1) ;

2) ;

3) ;

4) для любыхиз.

Пример.По заданной вЕ_n системе линейно независимых векторовпостроить ортонормированный базис.

Решение.Полагаем. Векторбудем находить в виде:, где коэффициент

.

Тогда .

Находим вектор .

.

Находим нормы векторов .

Нормируем векторы . Получим ортонормированный базис: