1.3.4.1. Ошибку измерения определяют погрешности измерительных приборов

Если ошибки отдельных измерений ₁; ₂; ...; _n определяются погрешностями измерительных приборов, то можно дать только оценку максимальной ошибки. Теория случайных ошибок здесь не применима.

Ошибка суммы

Пусть измеряемая величина является суммой независимых величин (i = 1, 2, …, n), тогда, имея в виду сказанное в п. 1.3.2.3, можно записать

(30) .

обозначив погрешность определения величины Y через _Y, получаем

,

откуда

. (31) .

Относительная ошибка суммы равна

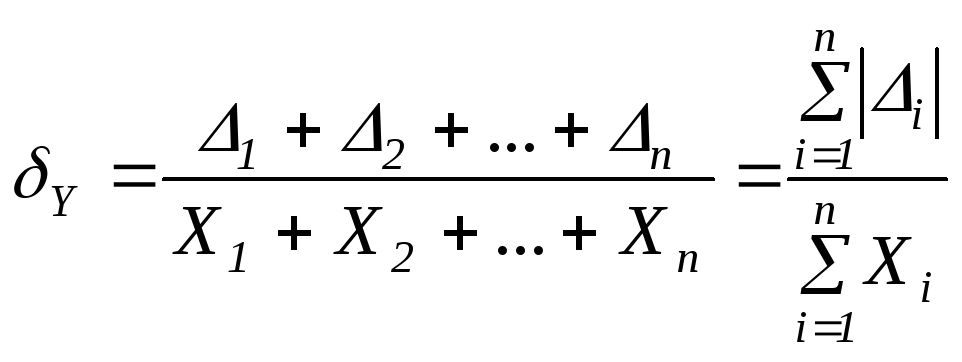. (32) .

Ошибка разности

Измеряемая величина является разностью независимых величин (i = 1 и 2), тогда

Сумма ошибок здесь берется по той же причине, что и в предыдущем случае. Поэтому

, (33) .

Относительная ошибка разности находится аналогично относительной ошибки суммы

. (34) .

Ошибка произведения

Пусть произведение измеренных величин имеет два сомножителя

, (35) .

или

Считая, что ошибки значительно меньше измеряемых величин последним членом в скобках можно пренебречь^* и окончательно выражение для _Y записать в виде

. (36) .

Относительная ошибка произведения может быть найдена из

. (37) .

Ошибки произведения с числом сомножителей больше двух, ошибки частного, степени, корня и более сложных функций могут быть получены аналогичным путем.

Удобнее всего для определения ошибки физической величины, описываемой практически любой функцией пользоваться следующей формулой

, (38) .

где - частная производная функцииf по переменной X_i.

В таблице 3 приведены формулы для вычисления ошибки измерения величины описываемой наиболее часто встречающимися функциями.

1.3.4.2. Ошибку измерения определяют случайные ошибки

Теория ошибок дает для определения средней квадратичной ошибки S_Y величины Y следующую формулу

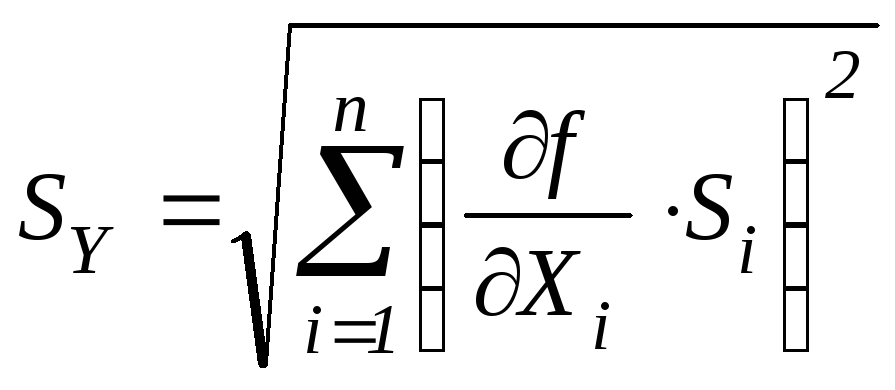, (39) .

Таблица 3

Систематические ошибки

№ п\п	Функция	Абсолютная ошибка	Относительная ошибка
1	2	3	4
1
2
3
4
5
6
7
8
9
10

где - средняя квадратичная ошибка ряда измерений дляX_i. Выражения для часто встречающихся функций приведены в таблице 4. Среднее значение получается подстановкой всредних арифметических. Доверительный интервал и доверительная вероятность определяютcя по так же, как и в случае прямых измерений.

Таблица 4

Случайные ошибки

№ п\п	Функция	Абсолютная ошибка	Относительная ошибка
1	2	3	4
1
2
3
4
5
6
7
8
9
10

Если сравнить таблицы 3 и 4 строки 5 – 10), то видно, что выражения для расчета систематических и случайных погрешностей, в которые входит только одна измеряемая величина (величина отягченная погрешностью) имеют одинаковый вид. Отсюда следует, что выражения (27 – 29)– частный случай определения погрешностей определения косвенных величин.

Пример: Для определения объема параллелепипеда сделано поn = 10 измерений каждой из его сторонa, bис,в результате которых получены следующие средние значения и средние квадратичные ошибки (в мм):

= 4,31; = 0,11

= 8,07; = 0,13

= 5,33; = 0,09 .

Определить абсолютную и относительную ошибки определения объема параллелепипеда для доверительной вероятности = 08.

1.Удобнее сразу воспользоваться формулой для относительной погрешности дляV = abc

=

==

=

V= 185 мм³.

Для n = 10 и доверительной вероятности  = 0,8 определим доверительный интервал _V. По таблице 2 для n = 10 определим коэффициент Стьюдента (t_0,8;10 = 1,4).

Имея в виду и соотношение(17) находим

.

Отсюда V=1850,016=2,97~3мм³.

2. Можно поступить иначе. Определить среднюю квадратичную погрешность для функции

==

=мм³.

Используя и выражение(17) находим _Х

мм³.

Окончательный ответ для = 0,8 записываем

V= 1853 мм³.

В практике измерений широко используют два способа расчета погрешности косвенных измерений (см. п. 1.1.2.), которые дают практически одинаковый результат.

Способ 1: Сначала находится абсолютная , а затем относительная  погрешности. Этот способ рекомендуется для таких уравнений измерения, которые содержат суммы и разности аргументов.

Если то согласно(38) общая формула для расчета абсолютной погрешности физической величины Y для произвольного вида f функции имеет вид:

(40)

где - частные производные функцииf(X₁,X₂,…,X_n) по аргументу Х_j; - общая погрешность прямых измерений величиныХ_j.

Для нахождения относительной погрешности нужно, прежде всего, найти среднее значение величины . Для этого в уравнение измерения(2) надо подставить средние арифметические значения величин X_j. То есть среднее значение величины Y равно:

, откуда .

Пример: Найти погрешность измерения объёмаVцилиндра. Высотуhи диаметрDцилиндра считаем определёнными путём прямых измерений, причём пусть количество измеренийn=10.

Формула для расчета объёма цилиндра, то есть уравнение измерения имеет вид:

Пусть приР = 0,68;приР = 0,68.

Тогда, подставляя в формулу (29)средние значения, найдём:

Погрешность _Vв данном примере зависит, как видно, в основном от погрешности измерения диаметра.

Средний объем равен:

Относительная погрешность _Vравна:

или _V = 19%.

Окончательный результат после округления (согласно п. 1.3.2.4) записывается в виде:

V = (479) мм³, _V = 19%, Р = 0,68.

Способ 2: Этот способ определения погрешности косвенных измерений отличается от первого способа меньшими математическими трудностями. Его чаще используют, если уравнение измерения содержит только произведения и отношения аргументов.

В начале находят относительную погрешность , и только затем абсолютную .

Пример оставим прежним.

Все численные значения входящих в формулу величин сохраним теми же, что и при расчетах в предыдущем случае.

Порядок действий при расчете погрешности косвенных измерений следующий:

1) Прологарифмируем уравнение измерения (логарифм берём натуральный):

,

затем находим дифференциалы от левой и правой частей, считая независимыми переменными,

2) Заменяем дифференциал каждой величины на абсолютную погрешность этой же величины, а знаки “минус”, если же они есть перед погрешностями на “плюс”:

3) Казалось бы, что с помощью этой формулы уже можно дать оценку для относительной погрешности , однако это не так. Требуется так оценить погрешность, чтобы доверительная вероятность этой оценкисовпадала с доверительными вероятностями оценки погрешностей тех членов, которые стоят в правой части формулы. Для этого, чтобы это условие выполнялось, нужно все члены последней формулы возвести в квадрат:

.

Теперь можно вычислить относительную погрешность, извлекая корень квадратный из обеих частей уравнения:

,

или в других обозначениях относительная погрешность объёма равна:

.

Причём вероятность этой оценки погрешности объёма будет совпадать с вероятностью оценки погрешностей входящих в подкоренное выражение членов:

.

Сделав вычисления, убедимся, что результат совпадает с оценкой погрешности косвенных измерений, полученной с использованием способа 1:

.

Зная относительную погрешность, находим абсолютную:



Окончательный результат после округления (согласно п. 1.3.2.4) записываем в следующей форме:

.