Собакин Е.Л. Цифровая схемотехника (УП)

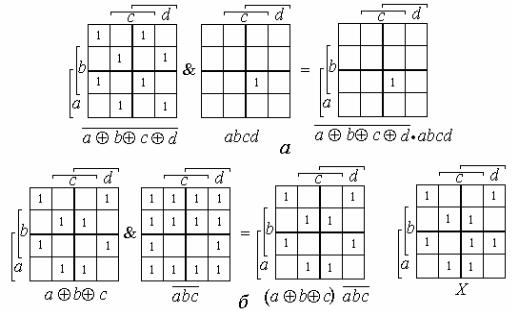
.2.4 $ " ! #, . # " " # ", '

«"» . - $ ! & #

(=). $ & 2' &

( .2.4, ) , ) # & " ! # «abcd». - .2.4,

.2.4. ) & " ! # (2.17) "-

! $ $ ' & 2- ' & " ! # (2.17). $ ,

) # " ! # (aÅbÅc).

& ", " ! (2.17) $ ,

! $ & " ! % /:

X = abcd + (aÅbÅc). (2.18)

( ') # * % .2.4 -

+ .

, " " ! (2.17) (2.18) -

') %$" , " &

* %, " ) ') #

. #. + " ! ' (2.18) "

..

$ * " & & -

" .

81

2.4. ) ( ) , "

, # $ $ 4-# & -

-# & «8-4-2-1» ! , «7-4-2- 1». " #' # -

# " % " &. $ $" -

# " #' # # # (

10), + # " & (

2), ! # # # % ! # 4-# " " -

. 5 $ $ # # " , &

" *%% " # ' " *%%

# " , -# " «8-4- 2-1». * ! # % *%% -

') & #. & # # &- % " "" #" + # "-

" «. " #», # # # -

. * # # -# " «7-4-2-1»,

& ! .+ " # , -

$ ". . 0 % $#

# # " .

# # " & #, -

& " " % ( . 2.1). $ +

# " " " & " #. ,

" " 3, 2, 1, 0 " & " -

" " & " (%) Y3, Y2, Y1, Y0.

2.1

+ # "

" " . 0 $ .

82

#, 3 . # , & -

% # " -

. ", ! # " " %

. " #, ') # " : 10, 11, 12, 13, 14 15. , " $'

+ " #, $ - # & #, ! " "$ # " " &,

" $ )+ " #. - -

" $, " " & " ( %) - ' " " # (~).

# &- #

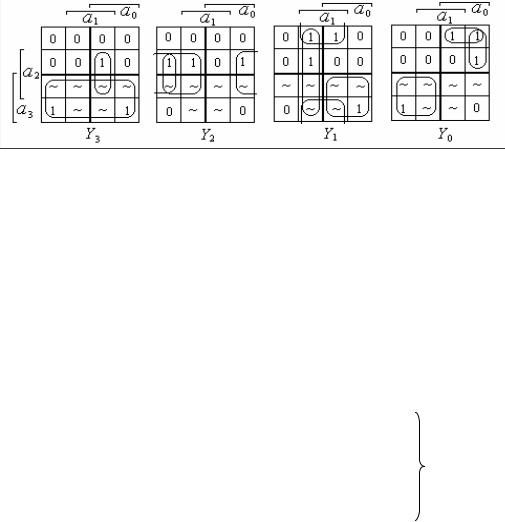
! ' % ( .2.5) , $.$ $ -

" , + - # ! %. " $

+ " " %, $# .2.1,

.2.1 # " '- ) # %.

.2.5. " " " % #

", " # % ! '$ , #.

* $# #$ , " ') ! $-

. " " # %.

# # - %, *, ' -

%, " # &

&.1. $" ! " # % # « -

» # # " #.

! %, " " # % " " "

$" . &, " .2.5 ,

') ' %:

83

( (2.19) # &-' $ -

& #. 0 " & ". -

$ .

$ $' "

& & . # !, $

& * ( 155. 4,

(2.19) % # { , 6, -5}. , ## *

", * $ + " ) !-

:

2.4.1., )$ ( ) , ) { , , }

(2.20) %$' .2.6.

# & # # & & " ! %$" + " &-

" ! # (% & " %) " " &

& *. (( & # 8,( * & $ #-

$ !) # (" #) " ' « "-

» . -

% Y0.

" ! ' % Y0 (2.20), , -

#') %, # # # 2' #. ($ , "-

" * * 26, & #- # 2' " " !. 8, * D2.3.

' $ " 2' " $ &

" ! 3 a0 , $ ! * 2 (D4.1), 8, * & *. 2' " %-

Y0 ! # 2' ' 3- !, +

!$ # # # & & a2 a1 .

($ , ' # * " 3 (D4.2-3) 26 (D2.1) -

. 3 & # # %$" " $" %. 4 ! " & * " -

& # 8,(. , & 8,( 5( " # #' # # «

», + ! ! -

#$ "$ # "

84

* . - ! 2.6 " " " - # & * + * -

". 0 " # %, #) #-

& " . " D4.2-3 -

!+ %, * 3 * 2 (D4.2 D4.3).

.2.6. $# # ( 91)

# ) # # " # # &

& " 8, * & ' « » - !. ( $ " *, " # *-

! " " " * ( #), ! " * " " * ( .2.6). ( & # " 8,(, " ) '

( ), " " ( ) !.

%$" ( # "-

$ $' & ' $ *, $, " ! & * ! «& !$» . (

85

! .2.6. - ! " -

# " " * -5 (D1.1…D1.4) «& ! "» $ -

') *. 5 # # # "$

" 1556-1 (D1), 155661 (D2, D3) 15561 (D4, D5), &

# 5 + .

2.4.2. , )$ ( ) , ) { - }

# # %$ " * --5

(2.20), ' " 2'.

" " ! # %$' -

# ( .2.7).

. 2.7. $# # ( 92)

86

( $' # .2.7 " " " -

# * + 155.

, # # # # 5

(D2, D5 - 155634; D1, D3 D4 - 155633).

( ## " 91 92, "

" . , 92 "- & # 91 $. -

. 91 # " " , -

92 & ( & * " '

! & ' % ').

$. ) & . # ! "$ &

+ & %$" & *. &

# )$# «.» &- -

& . , # !$ # # #

#, & % # . (" # '.)

2.4.3. , )$ ( ) , ( ) , ! )

% ' Y0 . # * & $ #

* % ( .2.8). ( " «#» + -

# $ " ! # (2.22) # % '

' ( Å) 2' (% # --5).

( + " ! # (2.22) (2.20) $' + -

* -6--5. & ') ' &-

' $ #:

Y0= a3 Å a0 + a2 a1 ;

-5) " #' * " 2Å (D1.2, D1.3) * " 2 --5 (D2.2, D2.3 D2.4). . #, " $

. &, " $ # ! * -

87

$ , % & a2a0 #

% & a2a0 . 5 !$ " 15565 (D1), 155633 (D2) K15561 (D3, D4), # & -

" & . # & .

∙" . #,

# " ! " " "$ « $ » ..

! & "$ "- " ') .

∙& * .

∙, " # .

∙.

∙$" & * " "

.

∙*%% " .

& * " # !-

# (* ) , ! !-

# . ,

$. &, &-

* $ ) " # ! ,

88

" ! "$ $ & *-

. " # ' # !$ -

. $. # , ).

# $ %

". &$ . $. " - & * # # , ". -

$ % $. " " , ". - &$.

, ! # $ & *-

& , * $ " &-

* + . # ) *

. , «.» & * " ". '

&$ , ". . # * !

$ ".

*%% " λ # # . -

" " %

& Q( − , " # ; , − -

" %. ) ! $ " -

" ' & ", *%%-

λ # $. (λ≤2). -" # " " " . 2.2. " $ "

$& # ! #.

, & " # %$# , #-

$ "$ " . 0 − # & * -

, . . $" .

,$ ' # ,

%$" $" " , ,

' ' 2+ %. *-

%$" +- "$ -$ ) ') " . -+ * -

%$" + $"

# $" .

89