
Собакин Е.Л. Цифровая схемотехника (УП)
.pdf
, * ' # % $# .-
# " # ! " . 1 & #
" & % # (8,) & *, )-
!$ & & " ! #
%$ , , %$ -
$ & " ! %, " ') " &
. &, $#$ # & " & ! " #$ * " # & " ! ,
", $ " " %$" .
& ' $ & % %, , .1.3 " " % " (- (- .
# #, & % # # # # ( 1), # - & % # # # «#».
- , % # :, # .1.2, , $ '- ) . " % ":
(- :
X = ab cd + abcd + ab cd + ab cd + abcd + abcd + ab cd + abcd. (1.3)
(- :
X = (a + b + c + d)(a + b + c + d)(a + b + c + d )(a + b + c + d ) &
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.4) |
& (a + b + |
|
+ d)(a + b + c + d )(a + b + c + d )(a + b + c + d ). |
|||||||||||
c |
|
||||||||||||
.1.2, , " ! (1.3) (1.4), ,
% # «1», + & - ' &.1, ! «0».
% ' # «# +/+»
& * « mod2». 5 $ $ -
" mod2 (% # V5 .1.3), !-
$ |
|
X = a Å b Å c Å d. |
(1.5) |
0 " ! * " ! ' (1.3). , ( .1.2, ), % mod2 + -
«. " » . 0 ! $ $- # $. " & % & %-
. , * % ' $" 2'- " 2' " % - - - .
# " ( & *, *
$ $ " % " # & %, -
" * *.
1.3.4. -* /, ! %
0 - " * ", ') ".
* " " ' # & % #,
" ' # % # -5. - .1.3 " 8, *
31

-5, " 8,(. , $ #
$ ", & & *. ( & 8,( ! $ % «1» 8,.
3 & " ! %
/ = a
|
# « ». " & * -5 |
|
|
& ! . ' # |
|
|
& &. 5$ $ ( &- |
|
.1.3. |
*, ') # & "- |
|
. - , ( 155 $ " 1556-1, |
||
- |
! ) + 4 & * -5 |
|
&- |
||
%- |
& $'. 5$ * " -5 |
|
". & $', - |
||
|
||
" ' # ! & " !. |
||
- |
6 & * " « » ! '
*- |
", " & # |
-5 |
& &. * " $' # # «#- |
|
» " & * # ". # &- |
.
1.3.5. -* /, ! %
0 * " ' % ' & & ! # (2'-
). # #' # " & "
" ' # ') & " ! #:
X = a&b = a b = a·b = ab. |
(1.6) |
( " 2' & # #$ ,
$. " & * &.1 $
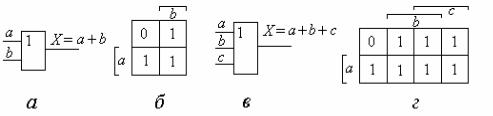
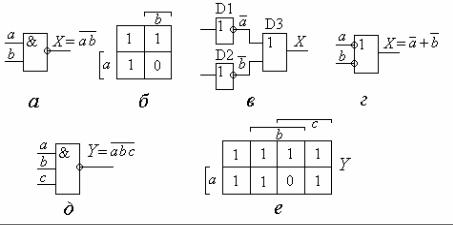
, " & " ' &.1. - .1.4
" " & % # " # -
& ( .1.4, ) + & ( .1.4, ) & & * .
.1.4. " & % # * : & ( ), + & ( ), " & % 2 ( ) 3 ( )
+ " " , 2' # &.1 $
, & & " − , ,
32
. . − ' &.1. * * "
" ' , ! # «2' "»,
" ') %, & − % # . # ( "- ' # " & * " , , 15561
! 4 * 2 ("). , ' # -
" *.
+ " .1.4, .1.4, ' ' # -
, " 8, '
.
1 & # " & $ -
$ , & & " * # #'- # , & & * !
$ $ " * . , .1.5 - " # & & * .$' (6 )
" * (2 ).
.1.5. & " & * : " %-
$" ( , ), 8, * .$' ( )
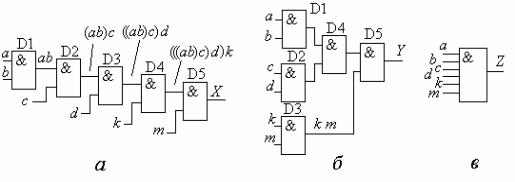
+ " .1.5 " & * " , '
$, * " & % ' 6-
& & & * ( .1.5, ). , " "-
' # " % & " ! #: |
|
X = ((((a·b)·c)·d)·k)·m ; . 1.5, ; |
(1.7) |
Y = ((ab)·(cd))·(km) ; . 1.5, ; |
(1.8) |
' * 6 ') " !:
Z = abcdkm. |
(1.9) |
: # # " & " "
! & # # "-
! # & & # ! $, , " !- # (1.7), (1.8) (1.9) % ' .
, " " ! # ! $ «&-
#» + " 8, * 6 .
33
( $, & " -
)$' " " !, , & ' # %-
. ' −
. # # " & ( "). (- #, " " " & # &,
& #' # # & # & %. ! # $" * " ' # -
& # # & , # &$, '
" ( " ') # &
" * . ( + &, $
.1.5, , # # &
, " & %, " "
$.. [5] ! # # " & % #, " ! #$ # # " -
!.
1.3.6. -* /, ! %
6 & * 6 # $-
" & ( " "). #, " ') #
* ", " # + ! % -
. - .1.6 " " # (8,) * 6
" " ') %.
.1.6. 8, & * 6 ( , ), " " 2- ' ( ) + ( ) &
3 & " ! & " " a b
" # ')
X = a b = a + b. |
(1.10) |
& # # 2' $# .
! + ! # " # # + (%-
& ! #), $ &, & *
% & " !. () *
$ $# $. # # 2'.)
34
.1.6, .1.6, , % # & & ! #
&.0 $ , & &- " ' &.0. 4 ! &.1 , " - & , . ., & " '
&.1. * * % ' " ' % 6.
!, 2' & ", 2' -
" $" $" " & ". -
* & # # # & # $ & *-
6, ! !$ # & " * 6 & " *, $. . 5
.1.5 * " $ " * 6 (26),
" ", " $ .1.5, "
# , " . ! ! $ &-
# " 8, * 66, -
" ! # (1.7), (1.8) (1.9) " & & ! #
+ (2').
" # ( ' # & * " 6. - -
, 6 * 155661, ! 4 * 26.
1.3.7. -* /, ! % -
0 * " ' "
&. & , * " --5 " ' # % « -
# 2'». & % " ' # %- # 7 %%, # # + $" « < », "-
" . 7 %%. # " # " $ $ #
# % 7 %% ( ) "- ! 2' ". - , & # %
% 7 %% & $ ') :
|
|
= a + |
|
. |
|
X = a / b = |
a b |
b |
(1.11) |
" ! (1.11) ' & !-
" !, + # $ " ! # (- % --5 (% # V13 .1.3). 3 " ! # :
« -
». 0 " " & ) " -
- $ ( 2'-
). - .1.7 " " & % # * 2 - -5, & %$# * # # -
%. ( # " % % --5, -
$, # ! " # "
%. ( ## " & " ! # % % --5, ! $ ') " ":
35
1.! "$ , #) ", & &-
( ) " (2' #) %; # "
. 5 & #
, * & 2'-
' . 5 ! & #
, * & .
2.! &,0, #) ", & ,-* -
&!! (2' #) & %, # " -
. 5 + & #
, * & 2' '
. 5 ! & #
, * & .
0 " " # " # (- (" ") (- ( ") " & %. (
$ $, # % 4 % * -
+ ! «#$» + ! ('),
% % + ! #$
+ !.
/, ! ' 70$ ' & % ' -
!,
.
.1.7. " & % # * --5: 8, * 2 - -5 !$ & ( ); % : ( ); %$# *-
# * 2 --5 ( ); 8, * 2 --5 $ & ( ); 8, * 3 --5 ( ) + % 7 %% ( )
/, ! ' " )70$ ' & % ' -
!,
.
36
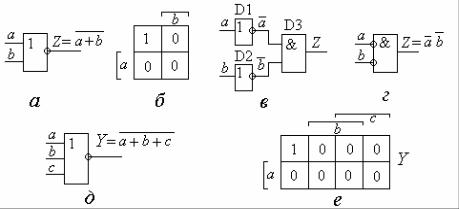
# $ * " --5, ') # -
, * , ! &-
". - , 155633 ! 4 * 2 --5
& $'. 155638 !
* 8 --5 ". & $' (
30, # & # $ 10).
0 2 --5 # # # " # -
& (6), . . * * ! #
" 6..
1.3.8. 8, ! % -
, " ') * 26--5, & " '
% # , # + $" ↓ ( ).
! # * % " ' « &
" (2')» % # 6--5. , -
# % # , % # 26--5 ') &-
" ! #:
|
|
= a × |
|
. |
|
Z = a ↓ b = |
a + b |
b |
(1.12) |
$. * % $
" ! & ". # $ " ! # (1.12) -
! ', « ! #
, # "
». 0 ! # # # " ) ! " - -
$ 2'. ( & " ! ' (1.12), * 26- -5 ! $ " & % # &-
. # !$ &, & . # $ &
%$ * ( .1.8).
.1.8. " & % # * 6--5: 8, * 26--5 !$ & ( ); % Z ( ); %$- # * # * 26--5 ( ); 8, * 26--5 -
$ & ( ); 8, * 36--5 ( ) + % ( )
37

&$ " ' # & * " 6- -5 " . ! !$
155651, ! ) # 4 & * 26--5, 155653
# * 46--5. * 6, * 6--5 " & ".
1.3.9. 8, ! % «3 #»
0 " * " , &-
«)» «.» ! "-
* &, & . * "-
# − ", " ' «%-
"». 4 # " & & ' # &
% & & # . #, #
" & &.0 # &
% . .1.3 " % V1 ( -
b) % # V4 ( ). - . 1.9 " 8, * « -
» ( ), & " ! %
& " %$# * # *.
= 0 # % Z ' & b. 5-
= 1 (# ) " * # &
&.0. , # # #
, b − % ". ,-
, ! 8, $ * « b» $ b -
|
", # ". 3 & |
|
& " ! % |
|
& b , &- |
|
! + . |
|
( $, * |
.1.9. 0 43 5: 8, |
43 5 " & ". |
( ), % « » |
0 ' $ , & " |
( ), * # ( ) |
$# #$ « ». |
|
6 & * " 43 5 "- |
|
' # &$ , |
#. - , 161 ( ,- - )
$ 16162, ! ) # 4 * 43 5 )
. - .1.9, & % (8,),
') & . # !$ &. ! $ 8, & . # $ &. # * & $' & & " ! # % «#$» ,
"$ &:
38
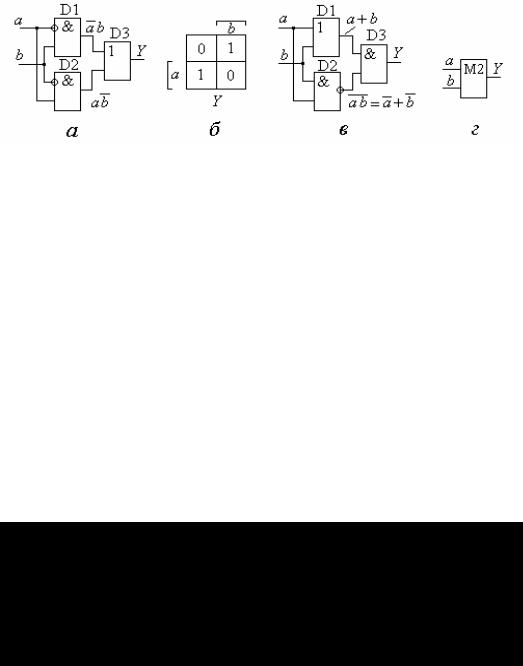
|
|
|
|
|
|
|
Z = ab = a + |
|
. |
|
|||
b |
(1.13) |
|||||
, & . # $ & & 8, *-43 5 #$ 8, * 26--5, $
$ $ .
1.3.10.-* /, ! % «&!! % ( mod2»
!% , *+ / *+
6 & # % # V5 « $» ( .1.3) -
&.1 $ &, & " ' -
.1. $ % & " & $ $ -
#, * % # $ ! # '
(mod2) " , ! ') " " -
&. # # * $# Å ! &. 0 %, ", , & "$ & ", . . $ $. & &.
3 & % " % ! # mod2 - & ' ') :
|
|
|
|
|
|
Y = a Å b = ab + ab |
= (a + b)(a + b ) . |
(1.14) |
|||
" " ! # (1.14) #' (- (- , -
. * % ! $ %-
$" * " " mod2 # . 0
", ! 8,, 8,(, * % " .1.10.
. 1.10. * mod2: " %$- " ( , ); + % ( ); 8, ( )
, , .1.10, $" 8, * -
* 26. .1.10, # 2' -
& + * 2 --5 , &, * " 262 . + " " . " ', %$"
# & mod2 ! $ $ !
39
"., .1.2, , " 4-
% ! # mod2. , ! "$ 4-
" mod2 " & % , - & " .1.10, (! "$ 4 ). " -
& " mod2 # #, " mod2 - & ". 4 )+ ! " &,
# . &.1, +, " & mod2
&.0, . . , - +$ « .». * * " « # +».
, $ % ' V10 - % ' -
, ( .1.3). , ! " # -
' mod2, $ # # # + . *
& % *, + ') &, $#
.1.10, .$ # " *.
$# & " ! # % -
(1.15), ! $ %$" * " " -
& mod2 " " (2Å--5).
|
a Å b |
= ab + a |
|
= (a + |
|
)(a + b) . |
|
X = |
b |
b |
(1.15) |
* % $# " .1.10, ,
$ ! " # ( $ -
, " − #). - $ " * %, $ &.1 + -
&.0 " " + &. ( " ! + ') « "».
&$ " ' # & * " 2Å, -
, 15565 ! 4 *. 5$ ", " #') % ' & & mod2 # " -
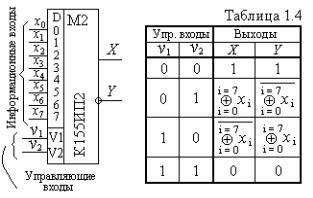
" ". - , 155 2 # # # 8-#
"/ " # " " "
# #') . ' # -
% # 8Å % # 8Å- -5. & % -
* " -
, " ') # ! " -
|
|
" (, " |
|
|
|
.1.11. |
|
|
|
.1.4, - |
|
|
|
" " & X Y, |
|
|
|
" |
)+ " &- |
|
|
|
" ! # +- |
|
|
" " " %. * |
|
.1.11. |
8, " 155 2 |
" ! , - |
|
|
|
||
40
