
Собакин Е.Л. Цифровая схемотехника (УП)
.pdf$ 2 «&
*%%» ') . 5 *- " 2', ') ! ", %$ - # # & " ' , ! " & (#) + *%%, " *%%-
# " . & ' ' ' 5- &
! $ ') " < 4 3 2 1 0>. ( ! ! $, #$ ') -
: & # " &,
') & # # (1), -
# " &, # # + (0).
" $
«!» % # ( -
) # ! ( #), " ! " -
#. 5 # ' -
#, + ". 0 # "
" .2.1, . !
$ , 4 *%% 24=16, 3 − *%% 23=8, 2 → 22=4, 1 → 21=2
0 → 20=1. - , 29 ' - ') # & ( .2.1, ): 4= 3= 2= 0=1 1=0. -
, (' 0 1) < 4 3 2 1 0> <11101>. # " * * $ 29, # #'-
) # # " " 4 3 2 a1 0.
- , $ ! -
# "$ + ! - !, . 5 * "
& # -
, 2' ' * ! . 5 ! * " ! & # -
, 2' ' .
$ % # "$ -
+ !, " + !,
') .
# + & , 29 -
%, * ' $ * # 2' #
a4 a3 a2 a1 a0 , |
(2.2) |
! * %, * '
$ * # 2' #
71
a4 a3 a2 a1a0 |
= a4 + a3 + a2 + a1 + a0 . |
(2.3) |
# $ " ! # (2.3) $ # 29
! % # !.
( ) # $. & ! # ) ! * . "
, " " -
# " %, + «)! * %!» . " - " $ «" » # # %
, " % # , . . # # %-
%. (, * $ !.)
)& ,-! * %' ! " ! ! )$ & % -
!( & " [3])
! !,
. (Karnagh), ! "
& . 0 ' ' # '):
1.2n * " , & n − &-
%.
2.. 5$ «& "»
« $"». 8 " ( & &) #
" & ( .2.1, "
% I-I). , # ! " " # #'- # # & &. - .2.1, "
% II-II # ! ' " )+ &-, . & "$ $& &, + &
. . ".
3.! # ' & * & # # # -
! % -
$ $ .
4.) " " # !- & & " & & " ½ ) ) ".
5.0 " ", ! " $
", " ' # « ». (( - ! " ' # ", #) #
.)
6.( ' & " ! #, - ') # & & $ & & ( ).
& &, & # & # # #
# $ .
- , * " " 12 13
( .2.1, ), ! " $ &
$ , # #') # & -
# & 0. 0 ( ) ' *-
" 2':
72

12 a4 a3 a2 a1a0 , |
|
13 a4 a3 a2 a1a0 . |
(2.4) |
(2.4), * * " 2' ' # $
0. 5, !
.
" ! ) "-
, (-, . , " #' $ & " ! # %. " ! # (2.4) ' - ', & " # ". * # ) #
# ! :
/ = a4 a3 a2 a1a0 + a4 a3 a2 a1a0 = a4 a3 a2 a1 (a0 + a0 ).
" ! !, ' , !
& & & «' + & $&». &
/= a4 a3 a2 a1 . |
(2.5) |
" ! (2.5) & ) & " ! #. 5 $,
" # %, "$ !
:
Y = (a4 + a3 + a2 + a1 + a0 ) (a4 + a3 + a2 + a1 + a0 ) .
## $" & " $ !- #, ') " !:
Y = a4 + a3 + a2 + a1 + a0 a0 = a4 + a3 + a2 + a1 . (2.6)
! " ! (2.6) $ 2' " , " &-
' 0, # -
. ( & ' + & $& * !
', * $ " ! * # ,
" !.
" $ - -
" #' # « $ » + # , " ')
" #, ! " " ("
). ! &, ! "$ $
", & « $ » " # # # # -
$ ". * -$ -& ' &
& %. " $ - - %-
, , !$# ')
# :
1.& $ * " " -
! ( 1, 0).
73
2.$ $ « » * "
2i, & i = 0, 1, 2 . . − # " !$" .
, ! "$ , , ", $. . .
3.! $
".
4." "$# & ( -), ! " $ &. - ( - ) $.
5. - #$ " , . .
'$ ! " -
%.
6.! " "$ " ( ) -
%.
7.$ « » & &$#
" + #, "$ « ».
$" « » ! & &
! !$ %,
& & % ) -
, " " . 0 ! $ #
" " .
$' + " % -
%, $ ~ ! '$ , -
" ') " # %, , " ')
%. * % # ,
" " $. ), . . " ! $. " " %. * '-
# # & " ! $' -
+ " & %. 5, " ".
# ! " & '$#.
,-* % 6 &$ - - "-
#, , (2') -
(2') # -
" .
,-* % 6 &, " ') & -
%, " # %" (&-
), & " # " " . * -
& # &, *
+ 2' ' , ! - ! & , 2' '
.
,-* % 6 &, " ') & -
%, " # %" , & "
74
# " . * -
( #) & # &,
+ 2' ' , − .
( # % " & %, ! $ -" $ % 5…9 &-
, . . "$ - - . # " -
.
-+ & , , % / + & ( .2.2, ). - , % , -
$ , " ! $, " $ -
" # % ( «"»), . 1, -
') & # , 2, ') &-
# b. ($ , * " &-
" ! # 1 2 . &, -
$ " " " ' # ", !
$ - %:
X = a b + ac.
0 , , " #$ & $ (- * %, ! $ + ' %, # '- ) :
X = a b + ac + bc.
.2.2. # & % $ -"
75

" ! ! $ .$ + "
) & ! #, , , +-
- − « »! % ' Y, ' .2.2, . -+ - , # * & ", " ') ". ,
" 2.2, . " # ". 1
& # ! & " !. # & " ! # #
2 cd # 3 ab, & - :
Y = ac + cd + ab. |
(2.7) |
0 " ! )+ ! $, # %: |
(2.8) |
Y = c(a+d)+ab. |
$ " ! (2.8) $ # # # $- ". -+ - * %, # * & # ", "- ') . ! , " %-
., " " . " #.
(3′) .2.2, .
5)+ # & & " ! # %- . 1′ ! a d , $ ,
$ " ! (a+d). 2′, !
a c , $ , " ! ( + ). -
, 3′ ! " + & # cb . 5 $ " ! (c+b). 3 & " !-
% - " + ! " "- ! :
Y = (a+d)( + )(c+b). |
(2.9) |
5 " ! ' (2.9) $ $" $
! #, & ! ') :
Y = (a+d)( + )(c+b) = (a+d)(c+ab) = (a+d)c + (a+d)ab =
= (a+d)c + aab + abd = (a+d)c + ab(d+1) = (a+d)c+ab. |
(2.10) |
, & " ! (2.10) $' "- ! (2.8), * , $ " ! # (2.7) (2.8) (2.9)
" ' ! & ' % '.
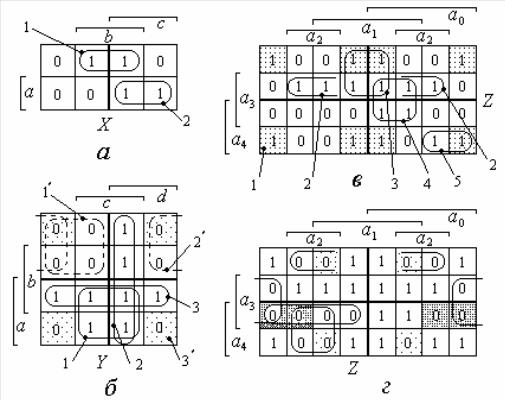
- .2.2, % Z 5- &-
, " " « ». , . . 91, " " . , 91 8 * "
( ), ! a3a2 ! & " !. 3 # ! ! & $" " "
, & " ! #:
92 a4a3 a2 ; 93 a4 a2 a1 ; 94 a3 a1 a0 95 a4 a3 a1a0 .
& " - %:
Z = a3a2 + a4a3 a2 + a4 a2 a1 + a3 a1 a0 + a4 a3 a1a0 . |
(2.11) |
76
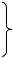
" ! (2.11) 2' " " " # - # " .2.2, . 0 " ! ! -
$ $ + " ) !. ( * -
#$ !
$ 6 ) ! * !! # " # -
( .2.2, ), ! " " $ " $ , "- ') ! "!? ,, & -
, ), 92 # -
, &, $
& & ( & # 1). ( $, " ! (2.11) , -
- % Z. & 93 ! -
$ a4 a3 a1 , & - :
Z = a3a2 + a4a3 a2 + a4 a3 a1 + a3 a1 a0 + a4 a3 a1a0 . |
(2.12) |
" ! # (2.11) (2.12) " , !
", ' # ! ( " ! (2.12) 6, " ! (2.11) $). -
$ " ! ' (2.12), $ 2-& 3-& 2' " $ ) !$ " 2 ( a4 a3 ). ## ' "
) !, " ! (2.12) ! )+ $: |
|
Z = a3a2 + a4 a3 (a2 + a1 ) + (a3a1 + a4 a3 a1 )a0 . |
(2.13) |
" ! (2.13) # # # "
$" ( { , 6, -5}) .
* ! %, + .2.2, , '-
# + - . - " # %-
" ' # 6-' . ( "
" " " . " #, « » -
. $' 2' ' $' % ( - ), ' , " .2.2, :
Z = ( a4 + a3 + a2 )( a3 + a2 + a1 )( a3 + a2 + a1 ) &
& ( a4 + a3 + a0 )( a4 + a2 + a0 )( a4 + a3 + a1 ). |
(2.14) |
|
# # , #$ $
2' " " ! # (2.14), "
.2.2, . , # ! " #, -
' (2.14) «'» % %:
Z = (a4 a1 + a3 + a2 )(a3 + a2 + a1 )(a4 + (a3 + a1a0 )(a2 + a0 )) . (2.15)
5 $ - (2.12) - (2.14)
%, ! $ " $ - . 3 &, ##
77

" % " (2.13) (2.15), ! ! ", % (2.13) $ .
" $ -" -
& « » , & " ' # - ! , % & !% (2' " 2' ").
* ! #$ # " %.
- , $' " .2.2, . *
, ') 4 3, ! " : -
. , & - ( -
). 0 ! «) ! '» & " ! # " , , $-
" " ' , ') ! # - -
) 2' " " a4 + a3 .
". " , ! $ & " ! # % $ { , 6, -5}, , -
, $ % ! # ' ( -
Å). «. " »!
$., ! %-
$" #, # % # # & % $ $# #, , , # #
% " .
2.3. 4 ' " &$!, ) " %! ! * ' !
- % #, " , ! " #$ "
& , # & " !. 0 #
#' '$ 2 " ., " & $
& " ! , ", "$ -
$ " .. $ , $#
& & # % %, !
$ $ $ & %, " .$
, " " &-
$'. , * ! $ -" -
& %.
"$ " & % #
% ! , & * % ' ' « -
$», . . # & & ! ! &. 5
% $. & &, + $
% ' $. & &. 0 ! $ -
&, ! # (f + f )= 1 2'
& & " ! # % # % '.
78

* ' ' & ' % ' ! $ % $. &
&.
- , $ % # F + & a, b ,
') & " !:
F = ab c + abc + abc .
! # " ! (d + d ) 2' " , " #
, ! $ * % ' ! % ' " + &-
:
F = ab c + abc + abc(d + d ) = ab c + abc + abcd + abcd .
* # & #, % # F &. ) - & d. " # ! "$ « » %,
% ' F $ . ". "- ! $ $ & & "-
! # % . & " 2' " ( ab cabc ) # #' # & " ! # , " ')
" . 0 " ! " -
$ ", #) & #
d. ! 2' " ' -
.
- % #, " % ! " #$ - ') & : + !, + !', mod2
.
# & " ! !, -
"$ " ) * ! &$' ') - ", )&, " )&,-
( $ . " ! " #$ $
" ! ! " & #
% #, # & " ! # $ .. ! .
# mod2 % X Y, - " .2.3, .2.3, . $ %$ !
$' & ' % $
.
, % # / % # + &. - " "$ " #, + $ % ' 4- -
& ( .2.3, ). + mod2 " %. # * &, # ! # mod2 (0Å0=0; 0Å1=1; 1Å0=1; 1Å1=0), -
" ') " !-
" # % ( :ÅY .2.3, ). 4 ##
" #, , % ( .2.3, ). 3 & ! " #$ & #.
79
3 & " ! % ! $, -
, ", " ') " ( "
.2.3, ):
|
= ac + |
b + cd |
+ bcd . |
(2.16) |
X Å Y |
" ! (2.16) # # # " «"», # # -
' % ' «.» .
.2.3. " % # %
)+ , . & ! !
" ' % # %.
# $, # & ,
$ " ! % /, ') & %:
X = |
a Å b Å c Å d |
& abcd + (aÅbÅc)& |
abc |
. |
(2.17) |
5 " ! $ , − " !.
" ! # (2.17) , % # 4- &-
. " 2' " 4- &,
+ &, ! $ % " +
&. " # $ " .
$" # ! " .2.4 ') -
. $ % # / 2', ! " 2'-
" " ! # (2.17) # + # ("
#). * $ ". ! #
80
