
Собакин Е.Л. Цифровая схемотехника (УП)
.pdf& & . #. * $-
. -! $" #
«)+ "» # " & ! + - ! ' & ".
, ) % # &
( & &$, ' ! + ! ". , *
# ' # # « » % # ! & & & *, & $ , « -
$» . ( .2.9) # "
mod2, * --5 -6--5. 3 " #
') $ . % ' # # &
. , .2.9 & " " -
# 3, 2, 1 0. 4, # # &
! & *, ! & ' -
& ", #' # & " ! & «&» *, ! & ! & * "-
" *. ' # # " " &-
. (- .2.9 * # ! " & " .) -
, !+ $ ' ' 97.
2.5.1. * ) !$%& '
" ". " #' !$
" ! − . * « -», . . & % # & -
& &, ' # , $" & * " ' " ". ( ! #
!, & * " #' + # « », &. * &-# $ "
% . - * & # # & (&) &-
" " , $ " &
& & ! " ! "$ ". * " - & * " " «# ' #» ". 0 #,
&
& ", ) ' !$ - %& '. $" # # & -
'. , ) ' #, " " " & " ( -
) & $ " # &-
% # . #. # #, #) -
. # & & % #, " ' # * - ! ) !. $ " ' #
, " ' # # (# « »), " #.
91

" # # + " # ! %"-!!
" . # & − * -
& & & * &-
. $ # & & * !- # & " & &, " & "
" ' # " (") & # "- & & *. !, # ! " , -
" & " " ' # ", ! " "- " &, .
! " # -
, " & " " ' '
. ( ), # « » -
" % " . ! ' #
* # & $ , ..
" # #-
. , # « », " '- ) % #:
X = a × a ; Y = a + |
|
. |
(2.25) |
a |
( & & " ( ' + & $&)
% # / ! ! "$ &.0, % # Y − &.1.
$# * & .2.10, .
!, & # # &, * " D2 (2 ) D3 (26) ' ) >$. "
' * -5 (D1), # * & # "
& " ( .2.10, ).
.2.10. # #
&, $ & ! # # #' #
$ &.1 " * D2 $ &.0 " * D3. 0 # # & (2.25). -
&, & ! + %$ " # # -
$ #, − % & & ( t0) $ " /, ( t1) − $
" Y. + $ " $ #$#
92
! # &.0 &.1 ! " -
# # * -5 " " *.
" ! # (2.25) ' ' &-
! # # - #, − &- &
' " ! #
F = f1·a + f2· a F = (f1 +a)(f2 + a ), |
(2.26) |
& f1 f2 - & " ! %, -
! " # #. $ , & # f1 f2 - " &.1 ( &.0), " ! # (2.25).
, " # #:
" − «#$» " ! -
&;
− " " & *, " ! " -
$" #, '$ " %$", -
, & ') RC- .
" & * '$ -
&, " ! # " "
! # & & * ". - , -
.2.10, " « 1» " '$ -
! #, ! # &
D1.
" " * D2 D3 '$ - & ') RC- . ( "$, # -
& ') ! ".$ & $- & #, " )+ # $ &.0
') *. - , # 155 $-
, ' $ & & *-
, ! ".$ 2&. 5, # - ' # $" «"» ".
( ) 3- −
! . ($ * & .
' % /, .2.2, , # " - . + $" ,
" ') " bc ( .2.11, ), $ + &-
" ! * %. (( # *
«.», $ " # % "- ' # & # .) $ ') " !-
:
/ = ab + ac + bc.
- * % " ! ! "
.2.11 (1) (2).
93
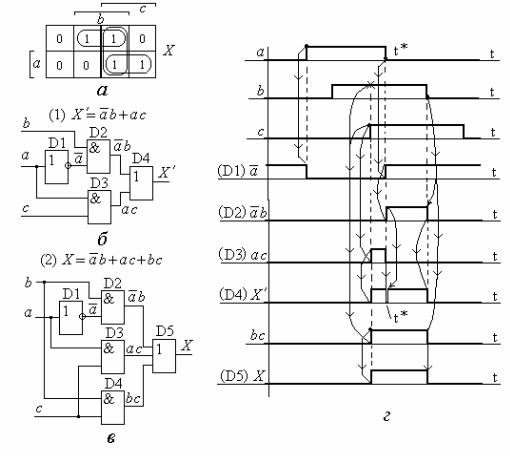
%$" " % "
.2.11. # %$-
"
" ! #, .2.11, .2.11, . 4, .$ -
$ $' # " & , b ( .2.11, ),
" & " & " ! & - " %$" & *. -
" & " # & * $ & " ! #, "- ') * " " & ". &, # & &-
& ! & " # -
. & " & ' # «# " ' #»
.
& " & & /′ (* D4
.2.11, ), t* & & $ &.0
#. ! .2.11, # # -
', $ & «bc» " * D4 t* - # & #. .2.11, .2.11, -
94
%$ "$', # ' ! % ' (/ = /′). , & & " ! #
(2) " ' # !, $ -
. & # #
& " - $.
, " &$, ' ) % * ( ) , & * ) ,-* & '. 0 "-
+ # " # ' " − " -
$".
) ! ' # ,
-
$ «')» . , -
«bc» " .2.11, # # #
'), $ & # $ # $" -
# # .
( !: , & ' &$, ) % *, " * ) '.
( $, % # %$ « » « » & & (% ) . *
# # & "&$ !$' $. ,$
.2.10, . 5 * 26 $ $ * 26-
-5, ! ! ! & & .
+ " / $ &.1 # # %, " Y − ! $ & & .
4 # " ,
+ # )+ (2.20) # -# &
«8-4-2-1» «7-4-2-1». , " ! % Y0, − + # #
3. * 91 " # -
$ $" − !$ # # -
& # " & & Y0 # & &-
3.
2.5.2. . &$, %! ! ! $%& '
". " ! & " " %$"
& (% ") . " $# #$ & $ #$ ! %$" , -
$# ! %$" .
&$, % !% " ,6 % (!$) 7+!
!$ & ' , " ", & ! " (-
, )$ %( , !%& ' ! &$'.
95
$" " $' # ! !-
& $ $# ! -
, ') & *.
&, %$" " # #' # ! " *
# $' $" .
) ! %$" 2# #' # - ') #.
1." & % # (8,) %$" *-
! " $ # 8,( 5(
(5 " ), 8,( 2.74391 8,( 2.759-91. 0 # 8, & *, -
* ( , , -
, * . .). * 8,( &-
# & *, # #$ %$ & 8,, #$ # 8,(.
2.6' * ! " $ " - % " #. 0 # ! " $ 8,( 2.710-81 «, # -% " * ». - %$" * # # $ ),
" # # % ! *-
. , " # & & *, #$ $ ", ' -
.
3.5 8,( & 8, * %-
$& , #$ ') 8,(, $#
$ ') 8,, %$" (*)
"$ $" , %$ & 8,, ! ') # #. - , " ' # % ", * " '-
, &$" " * " ! % & " -$" .
4.$' " ' $ & "
" " ". * * " -
& ' . " # " '
!, " " # - !. " # ( # " *)
& ' & " .
5." , # ! # " -
, # ( #) * !-
$ #, " ') # &. - , «(», « », «4$» . . $ ! ) "-
$ % & " *. - , "
96
$ , ' $ $ $ , ') %-
" , " $& &.
6.6 # ! * .
" ' ) " " # 8, *.
* , " ') #, %$- " . 0 &-
. 8,(, " # . ' #
.
7.# ) # ! %$" $ $#
# & # («!&»). 4
. * " (& " «6-&» $ -
" " " . &, " (& %-
/, * " !&. & , #) #
!& " #) # !& ! " $ " #, * # (#) ! " "$# !&.
8.$" " " ' # ' # .,
" 8,(. , " 8, * -
! " $ + " 8,(. 5 -
# 8, 8,( # #, $
" 8, *. # * " $
$.$ $. ' ! ! " -
$ 8,(.
$" " " &$"
, , ! % ' # , -
$" # # . * " # #-
# ! " %. -
%$" ! $ $
, # "$ , #'- ) " #.
2.6.) ($( , % ! $%& '
, ) * ($( , % − $ % ', -
' # # (& #) . -
$" "$ #, "
. , * − #
, ! .
* " $" %$" # # # ! # ,
" * , $" #
# . 0 # 2+ !
$" . * ! $"
&0 &0. *+ % − + # )-
97
+ " #, ! "$ -
, & " $ $' " -
.
% ! ! " ' # #
#, # ), "
# * , # # +! - " " # & #.
, % " &$" $-
. $' $' # # % % %
# # %. -
# " *-
" (() & "$ " " " . - , #
" $" " # # #' # -
# # )$ $ " ", + " $. & " ". #
" ! " # # #' # + $, ! "
( $. # +!$), !$ " #') # -
# . . , ' $# "-
$ ., $ " $.
') #! #, $ " "-
" $. # +!$, # $ " &-
", . .
1$. " ! $,
* " "$ " % ",
& ". " &
# # ' ". "
. " # ( %$ "
" & * , $. #. ( " ' " ' $ % - & , %$ . * )
!$ # ( ' & & '
" "& , ' & & ', # # " -
.
$. ( - & ' $' , -$" " # &$" . 4 +
# *+ & ( , ! ' ! . *+ & %-
" ', & ! # - " & ( ) " (% # " "
). # " # " + # -
" .
.2.3 " " * ", $ - " + $" 6
98
6.. # [8]. + " $"
, , & $ % $
% $" & # " -
! " " & * (60).
& * " ' " !, & " - #! # #' # ( ). * "$
& " # #!, " " " ' # #
( ) * # # &.1 # &.0 . 0 -
# (U1 U0 ) " . 2.3. * - # " # #. &, ! " '- # " " %%$" # "
*. 0 # (R1 , R0 , R1", R0") #' # -
# & " & #! # , ,
".
. 2.3 " # ( 6 155 & -
# (( 6), ) 134 (6) 6. 531.
", $. ' ' - " 7 . #) # " # .-
# # ( 6. 1533, # #') # # &
531, 555 533. # #
# $ " * "
, + " .2.3 " ! $ $ #
!+ " +.
, " # # & " # #
, # $ #
( " , , - # " &
%$& . # -
$ ( " , & #
& &.1 &.0 ' & ' $. ( & & ) # # )$' "-
" & %/, ! ( & *-
". & $'), , ') #
. .2.4 " # &-
( " 6.
* " " # " " & * (60) * ". & $'.
*+ # ! . " + # # -
& !. * # # &!! ! . ', -
# " ! $ .
" # # !.
# , ') ! ' %
f, $ " ! * &0 ( , !&0 ! ..
99
|
|
|
|
|
|
2.3 |
|
|
|
|
|
|
|
||
|
|
( # |
|
- - |
|||
|
155 |
130 |
134 |
531 |
|
||
|
(( 6) |
|
(6) |
(6.) |
|
|
|
I1 , # |
-0,8 |
-1,2 |
-0,18 |
-1,0 |
. &.1 |
||
I0 , # |
0 |
0 |
0 |
0 |
. &.0 |
||
51", ( |
4,2 |
4,0 |
3,8 |
4,5 |
" #!. . |
||
|
|
|
|
|
&.1 & ! & 60 |
||
50", ( |
0 |
0 |
0 |
0 |
" #!. . |
||
|
|
|
|
|
&.0 & ! & 60 |
||
U1", ( ³ |
2,4 |
2,4 |
2,3 |
2,7 |
" #!. &- |
||
|
|
|
|
|
! & 60 . &.1 |
||
U0", ( £ |
0,4 |
0,35 |
0,3 |
0,5 |
" #!. &- |
||
|
|
|
|
|
! & 60 . &.0 |
||
|
|
|
|
|
& . #!., - |
||
U1 , ( |
1,5 |
1,4 |
1,5 |
1,3 |
. 60 |
||
|
|
|
|
|
. &.0 . &.1 |
||
|
|
|
|
|
& . #!., - |
||
U0 , ( |
0,5 |
0,6 |
0,8 |
0,7 |
. 60 |
||
|
|
|
|
|
. &.1 #. &.0 |
||
, ( £ |
26 |
49 |
2 |
16 |
. . )$ |
||
|
|
|
|
|
60 . ! |
||
R1 , & |
10 |
10 |
10 |
10 |
%%. . - |
||
|
|
|
|
|
60 # &.1 |
||
R0 , & |
¥ |
¥ |
¥ |
¥ |
%%. . - |
||
|
|
|
|
|
60 # &.0 |
||
R1", & |
200 |
180 |
190 |
150 |
%%. " - |
||
|
|
|
|
|
60 . &.1 |
||
R0", & |
0 |
0 |
0 |
0 |
%%. " - |
||
|
|
|
|
|
60 . &.0 |
||
U . , ( |
5,5 |
5,5 |
5,5 |
5,0 |
$ |
|
|
|
|
|
|
|
#! 60 |
||
U . , ( |
-0,4 |
-0,4 |
-1,56 |
-0,4 |
. - |
||
|
|
|
|
|
. #!. 60 |
||
I". ., |
10 |
15 |
1,8 |
8 |
$ |
" |
|
3 |
|
|
|
|
" 60 |
||
F ., )*! |
10 |
30 |
3 |
50 |
$ |
# |
|
|
|
|
|
|
' 60 |
||
³ |
8 |
10 |
8 |
10 |
*%% |
# |
|
#! ' |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
" "., ( 6 ' 60 -
# # &.1 # &.0 ' " , -
100
