Собакин Е.Л. Цифровая схемотехника (УП)

" # # & % -

%$ " & *-

, ! $ " $' % -

. (% " ) $ $"

" ".

«# "» " # &-

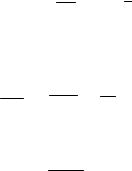
% %$ " " 60.

* #$ { , 6, -5} -

" .

( $, ' %- &.1 &.0 & * (" ). -

&.1 # ' ') & &- & * . &.1 ( ' #), %-

#- &.0 − ' ) ' -

# (&$# «#», . &.0). *, & # &$'

, "$ %-".

: ) { - }

0 % 7 %%, %$ " -

$ * --5. ( # # # #

% # 7 %% (" ! 1.11):

X = a / b = a b = a + b .

( & * " ! ', ! $

, 6 -5 # 7 %%. 6 & $, a = b

$ ! . ,, 2' ' -

" a b ! $ ') :

# 2' " a b #$ '

' «"$» &:

- .1.19 " ') " "

& . + " , $. -

" ' # ' & ".

+ " .1.19, " ' # * 2 - -5 & * ", ' . &.1 ( ) $ , # " ) & &-

& * + # # &. ! 2-

+ # # &.

51

( & " ! ' * 2 --5 3 --5 %$' * '

! & * «³2 3- »

: ) { - }

0 % # & - 2'

% # . ( ') # % %

" ". (" ! 1.12) 8, * 26--5

.1.8, .

Z = a ¯ b = a + b = a × b .

5 * " ! !$ a = b b = 0, ! $

, 2' #$ ' ', -

. { , 6, -5}

52

{6--5} + ! &

& $ & & #, ,

# # $ % ' !

+ + , # :

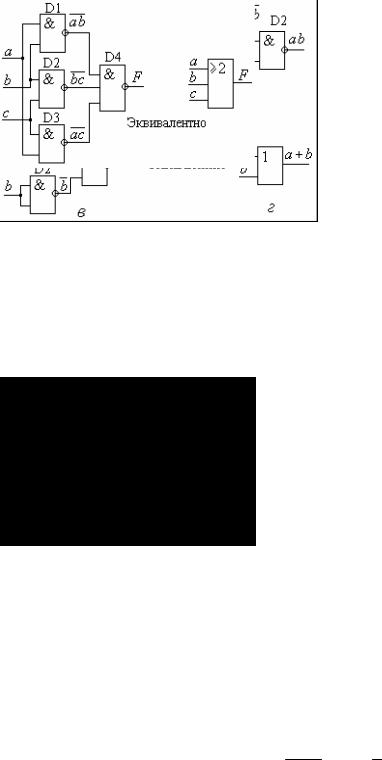
( & " ! ' (1.29) .1.21, %$# *-

# ! & * «³2 3- ».

- * ! "

" * 26--5 % ,

2' 2'. ( # " !-

& * { , 6, -5} { --5}

{6--5}, ! $ '-

$ { --5}, -

$ * #

" & *,

{6--5} – $ &-

%. , ! & *-

.1.20 ' # & ": 155633 ( -

" * 2 --5) 155634 ( * 3 --5),

.1.21, – ": " 155651 ("

* 26--5) 155654 ( * 36--5). , " ! -

& " ! # % . , -

## " ! (1.27) " ! (1.29), ! ",

53

! & * " ! ' (1.29) &

!, $ + $ $..

: ) {&, Å}

0 # % # - + ! (&)

mod2 (Å), %$ " *

& " * & " * «

mod2». , & * " " " ".. 5 $ "-

! % «! mod2» 2',

2' (" ! 1.14), ! #$, - # #. - , " ! % «!

mod2» ') :

Y = a Å b = ab + ab .

5 !$ b = 1 $ * & # +-

" !,

Y = a Å 1 = a ×1 + a × 1 = a + a × 0 = a .

, * 2Å # $ & &.1, * " #$ % ' (* -5). 3

!$ b = 0, $ * $ & &.0,

mod2 " #$ % ' # (&-

$ $ #).

$# % ! # ' , ! -

$ & " ! # " ., " #

{ , 6, -5} {&, Å}:

Å 0 = ; Å 1 = a ; Å = 0; Å a = 1; a + b = Å b Å ab. (1.30)

" ! # (1.30) & b ! $ $ - " ", ! " & " ! # (%).

( $, mod2 & & ! &, #- & + , ', ! & # +

, mod2 &. * -

# # * % - «+ mod2».

% ! «³2 3- »

{&, Å}. & " ! * % :

F = ab + bc + ac.

$ ' " ) ! -

" 2' 2' " mod2 - & " ! # (1.30). &

" ! ' %$' * '

! & * {&, Å}. 0 " -

54

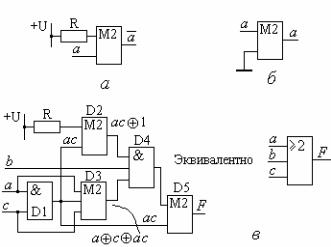
$# * 2Å * -5 #, !

# % 26 " .1.22. - .1.22, .1.22,

, ' # * -5 $,

.1.22, - ! " *. , % & " *-

D1 D3 ' ' * 26. &, * ! " " . &.1 &.0. 5, ,

$ ! " * .1.22, -

155, !, { --5}, # & .$ -

": 15565 (" * 2Å) 15561 (4 * 2 ).

+ * 2

# $". , -

'-

«"» , " $ %, -

«! "», " $ " % # -

! " % #, # ) )$ -

. # " .

, ' (* &-

& & «=2 4- », .1.14, ,& ) " %$#

.1.14, , # " ! ' (1.18): Y = (aÅd)(bÅc) + (aÅb)(cÅd).

0 " ! «"» , $

& Å $ # 2' ( +). 3 &-

" ! + % (- ! " .$

2' " , ! " " # " 4- !.

(- + " ! ' # " &

" & . ( $ " $-

" ) !

+ mod2.) 8 ) $ $# % - # % ( .1.14,&), " " " {&, Å, 6}.

55

: " , ! $ !$ -

% $ % ! # mod2, # # # ! ( ) «. #», . . « » .

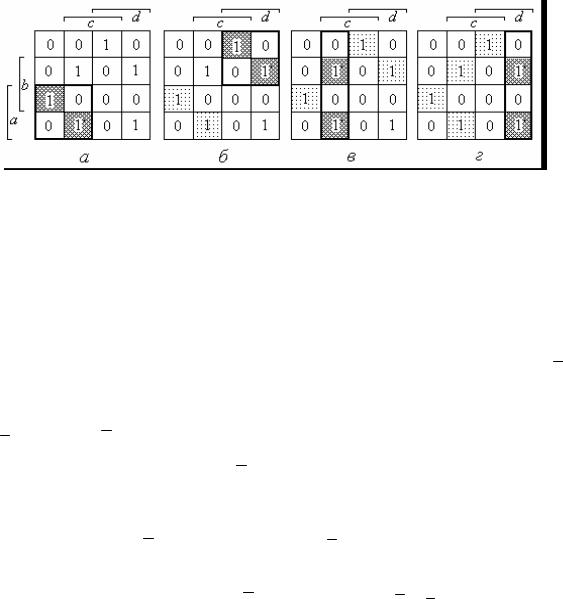
- . 1.23 ! " $" #, ' ') #

«"» " % " «. " -», " " # mod2 ') &.

.1.23. , " & & " ! # % & & - & {&, Å, 6}

$ , & # & & -

& ( + +¼+ = · ·¼· = ), # " . " - " & $#, * "$ " -

$" & " !.

$ & " ! # , "- ! % "$ 2'. " . "

.1.23, , , & # $' ad .

" b c ' ! " #, * *

mod2 " &, ! #

ad , $ ad (b Å c) . 3 & .1.23, ad(b Å c) . -

.1.23, & cd (a Å b) cd (a Å b) . -

, " # % " ". $ ! -

$ & " ! %:

Y = ad (b Å c) + ad(b Å c) + cd (a Å b) + cd (a Å b) .

' " ) !, &

Y = (b Å c)(ad + ad ) + (a Å b)(cd + cd ) .

' $ " " " ! #

mod2, , & a, d c, d. ,$

Y = (b Å c)(a Å d ) + (a Å b)(c Å d ) .

56

: , -

$& . # & *, "

. . , # ( 6 $ $

(8 --5).

4 «& ! #» & * – & -$ " – # & "$ $- " " & , " # " % " ,

, " # % " ( $' # & "

( & * ", , * & " , *-

" ') * ", &$" " . .

&, # & * & -

" + !$ #$ # -

& * # ), " #

& & ".

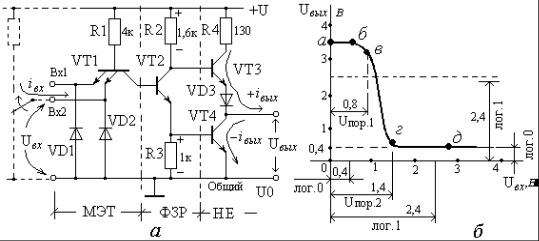
$' . & & * 2 - -5 ( .1.24, ), " & " «"» (( 6). ( -

+ : # $ (0) – & * " VT1,

. 1.24. 1 " * ( 6: ) -$#, ) #

& # % # " & " &.1 ,

! #, % # 6 & " &.0. , " &-

& * " * " " n-p-n. ( ! ' “ ) ”. +

R1 # ') #!. *,

* & &.0 ( '

! “ ” ) ' # U0), - #! &.0 + VT2.

# $ " # % ) #') % )-

(4). , VT2 $" &

* ( " R2 R3). -

58

$ * n-p-n , #! &.0 -

. «"» #!, *-

#! &.0. $# $ – " VT3VT4. , # «! "» (* -5). -

" # # * ", & ".

# &.1 VT3 ", VT4 ". *

" * #! & " (&.1). #-

&.0, , VT3 ", VT4 "

" * #! & & # (&.0). - $ #! # # 6 5(, *-

" & * #! &.1 # -

2,4(, #! &.0 0,4(. - . 1.24, -

# # * ( 6. - "

& % " " .

– # ' &.1 # #, & * & ! (" * '). –

# ' *, & VT2

"$#, $' )+ " #, * VT3 «

" #», VT4 « " #». – -

!, & # &.1 # # #

&.0. * ) , & «+U – -

R4 – VT3 – VD3 – VT4 – ) '

# U0» $ " " « ». 0 # !$ , «'» * -

#! # #$# $. , $ , -

# >$. # )$. " '$ * «.»

* &, ! ' 6 «. '» '

+$' $ " % " (~ 0,01'), -

(10…20 ..) . # . ' -

+$' $ % ( 10'). ",

* &, #! #$, ' , '- ) ' & *.

, , – -

# ' &.0 & & *. * # VT4 - " $' # ! ") #, VT3 ".

* " * #! ' ( 0,4(). - & % * " " # & - #! #, ". " ! ' # # - & & *. 5 * # # &.1, +

" #! U = 0,4(, !$" $ -

$. U .1 (& #!, . -

.1.24, ), * + # # &.1

# &.0. ( & ", * # #

59

&.0 ( .1.24, ) $" $

, #! # $. U .2, * + # # &.0 # &.1. -

, * & " #! # '

& *. )+ ) . , -

– , " $. & . 5 "$ «' » & & *

* & & ( ') & & - #! # ) #), * ! $ $ $ "

" &. , # 6 « -» & * " " $ $" " &-

" *%% # 10.

- .1.24, " " # * -

& $'. * ! " * +

«'» & # *, & + # &.

$ * " ", *-& & "

" VT4, & ". 5 $,

$ #! # # 5(, R1

" & * & $ 4&,

-* * & ≈1,6#. 0 -

# ' &. $ "

VT4 # $ 16#. , -

# & # $ & & * 10.

# R4 (130&) " #, # # -

# " * " "- # " « », $ ) ' ') & - #! #. * * " # ) " %, "

VT3 ". #. &, R4 &

" ') & (!$&) " & . " &-

& * ' # ') , - " # 10#. " ". #, -

$ '$ (1,2…2,4) &.

VD3 ! # # $& #! # ) #

VT3 " , & * - ". " ' # # " & # VT3

# # & & *.

" VD1 VD2 " ' % '), ' "

. ' # ') & #! # " #' ) ' % ' – #' # $& & #!- # * " VT1 " ) ) ' & "-

#.

( " " * # 3 .=20 ( )-

, I = (1,5…2) #.

60