
Собакин Е.Л. Цифровая схемотехника (УП)
.pdf3 # " ! (3.21), ! " !
# ( ) "
$ .
3.2.1.!$% & ' ( ' & & '
!&, (, - ,
' # '-
) [6].
1."$ % ' " -
, " & " " % ( %).
2.,$ ! & ! "$
$ MS & #. # ! % -
# ! {h} , " % #
&.1 ! {l} , " &.0.
3.$ %$', $' " -
, ' % " " $ h
. &.1, " l . &.0.
,$ ! {h}, {l} ) & + ! # "
% ') ' $
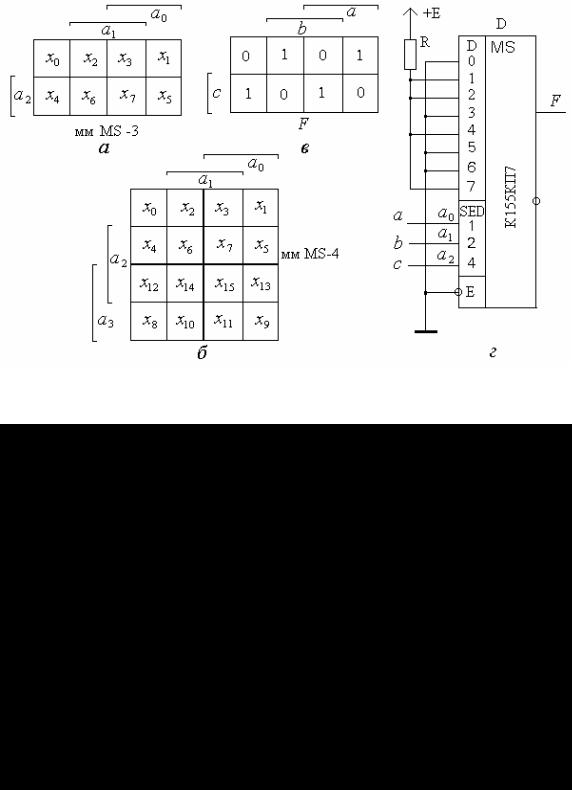
( . . S-3).
) ! , -
!, -
. ( ! !
, ! ,
! -
.
5 * , -&! , )& ! ' &$ , 1 * , " - % " %- !&, (, "- ( , ,
$ $ & #
$ $. & #.
$ $ " & " " MS
# # ! $ ! # ". "
" " & % (& -
" ).
' ' , #) '
" ( % " MS-k . &.1 &.0 " 1( $ - &
#, * $ - k-& #
(# .3.13).
- .3.13 !+ , & n M "-
. ( . ! !$
, + * " # #
131
«#» % " 1(
. &.1 &.0. 1 # $ -
(1() # -
i-& # , "
" % ()). !
|
" & ! # |
|
! & " % |
|
n. |
|
- .3.14 " ') - |
|
" $ $& + & |
|
# % « |
.3.13. # |
mod2» & a, b, c $ - |
" |
155 7. 3.14, , |
$ - |
% # + & # + |
|
# MS-3. $ - |
|
! # .3.14, .3.14, - |
#, % " " 1, 2, 4, 7 '$
. &.1, $" − . &.0. & % #
# " $ . !
! {h} {l} " {h}= {1, 2, 4, 7} {l}= {0, 3, 5, 6}.
.3.14. ') " $ - $& ( )
+ & ( ) #; & % "
mod2" ( , )
132
,, ! ! $ ! -
$ . * !
.0 .1 )! ( ( , 6 , . . "
l '$ . &.1, " h −
. &.0. $ " " $ , " -
& ! «. #», ') $ &-
& # (&.0). - " ! " $
') & % & " #, # -
$ ! # ". " ( .3.14, ):
a0= a; a1= b; a2= c.
( & (3.21), # $ k-& #, ! $
+ ' & k
. , $ & # -
" " , " ! "
% '.
# # $ - &
# $# , & # - " " .
- , # $ $ - 6-& #
(MS-6). 4 . )+ % & " - " $+ ') & ":
~ ~ ~ ~ ~ ~ |
~ ~ ~ ~ |
~ ~ |
]i . |
|
( a5a4a3a2a1a0 )i = [( a3a2a1a0 )j |
×( a5a4 )k |
(3.22) |
||
& " ( a~3a~2 a~1a~0 )j " " .
# ! $ $ 4-& # (MS-4).
* % " " $
& # (MS-2), ( a~5 a~4 )k ! $
$ & #. , # # S-6 -
# " $ + & # $
& #, $ . " (3.22)
#' # ') : i {0, 1, 2,…63}, j {0, 1, 2,…15}, k {0, 1, 2, 3}, ' % " $
. &, + & & #.
" * " ( 155, &
(3.22) %$' $ S-6 # -
( .3.15). ' $ ' $"
+ & # D1, D2, D3 D4 (" 155 1). %-
" " # #' # % " MS-6. # $
D5 ( 155 2). 155 2 #
$ - & # ) "
# " $" ". ! " $ ,
133
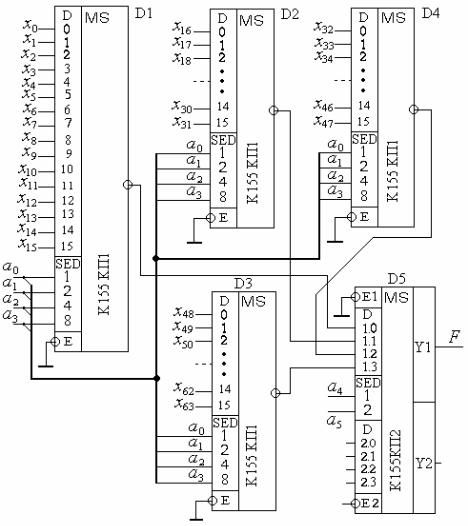
$" 155 1, $" "
#. - .3.15 8, $ D1 -$', " & % # $" $ - & ! " )+ %. , -
D5 $# $ " $ . " $ -
" ! . # , - ') " $ & &.0 ( ' *
) ' #).
# % " $
% % " " $
MS-6 # # # ' # " D1,...D4 % " $ D5. - .3.15 !+ .$
" , & " $ D1 ' %-
.3.15. $# $ - . & # (
1( # % 6 &)
134
«1.0», " D2 ' %
«1.1» $ D5 . .
, : $" - ' " " ", " $ D5 #.
$ # * $ -
6-& # " ". &, '- ) ( 51) $ D5 '$ . &.0, -
$ & . &, ! $ * &
$ MS-6. ,, " $
" ", " S-6 # " ".
! & ". , .3.15 ! -
$ $ # ' & % 6- & − # * & $ ! {h} {l} "$
') ' # % " . &.0 &.1.
3 " " ' % $. & &-
( 6) ! $ % (3.13). $ * %
nk $ " (#) $ -
& #, " " # # k- -
, q $ .
$ " ! ", ! " ( -
& ' ( ' & & ' !&, (, , -
$ , ) ( ! , & $. #. ( * *%% " λ 1
2.) , , # $ &-
" ! # " " % " -
$ '. ') " $ 4- 5-&
# & " ') " - ') # ' " ( . 2.1, ).
" ! !$
, + % "
$ . &.0 &.1 !
*. + # -
') " (" " #) "-
& $ ' % ' ! $ -
%. !, #
" , " ' %$-
"$' * .
( ) " " !
$ , 1 (( & % ) % -
" % 5- . " !-
, . . #
!.
135
-" " ! $ -
$ %$" ! $ -
. $ , % " " $' # -
$ . 5 * " $ - " & ", , -
$ - 4-& #, ! " " $ #
% ! 20- &!!!
" ! !$, $
$ .
3.2.2. !$% & ' " "& , '
& & ' !&, (, - ,
3 &, # " ,
$ - ! ! $ -$ . & ! ! " .3.1.2
( " ) # " ' ')
*.
1.$ " # ) ') &-
"$, $ &-' -
$ ( $ " & " ! # - " %). ') * " "$ # ! " %-
$ .
2."$ ! & % -
$ & ! + ! # & $-
. 2' " & & & + " ! #.
3.#$ " * 92 ! & - " " $ - ') # , " " ! % " &, #- " " ", * " " ! # - % " " $ .
4."$ " * 93 * " "- ! " ! % $ &, $ - ') & " ! %.
5."$ $" & *, -
$') " ! , # $-
" & *, $ %$',
$' " .
- 5- * , # %$ ",
, " # # " , -, ! " # $ ..
# ! 3-4. ! " " # -
" * , " & %
136

Z = [ acf + acde + ab( e + g ) + d( c + b l )] &
|
|
|
|
|
|
|
|
|
. |
(3.23) |
|
|
w( k + |
|
) + h( v + w ) + vt ] + mn |
||||||
& [ hv |
r |
|
|
|||||||
- $ ) " & % Z.
, 16 − * )$ & ! + &
{a, b, c, d, e, f, g, k, l, m, n, r, t, v, w, h}.
: # % # %, , & -
$, & " {a, b, c, d} {h, v, w} # $. $'. 4, " ! (3.23) & -
$. &, # %-" F1 F2, &
$ |
|
Z = F1·F2 + mn, |
(3.24) |
& |
|
F1 |
= acf + ac |
|
|
|
|
|
|
|
|
|
||
de + ab( e + g ) + d( c + b l ); |
(3.25) |
|||||||||||
F2 |
|
|
|
|
|
|
|
|
||||
= hv w( k |
+ |
|
) + h( v + w ) + vt . |
(3.26) |
||||||||
r |
||||||||||||
" %- $ . # - |
||||||||||||
! {a, b, c, d} & " " $
MS-4, " " ! (3.25) " * &:
F1 = ac × f + a |
|
|
|
|
|
|
|
|
|
d |
× e + ab ( e + g ) + dc + db × l . |
(3.27) |
|||||
c |
||||||||
$# ') |
$ MS-4 |
|||||||
( .3.16, ) + * " " ! # . |
" ! |
|||||||
(3.27) " + " . 4, |
, $ |
|||||||
2' & , # $' -
%, . . + " #. $ -"
# ", ') , $
+ & %, # " ')
.
.3.16. ') " $ 3-& ( ) 4-& ( ) #-
( $ )
137

& .3.16, ') * " "- ! # % F1:
ab = 12 + 13 + 14 + 15; |
ac = 2 + 3 + 6 + 7; |
|
||
dc = 3 + 7 + 11 + 15; |
|
b |
d = 1 + 3 + 9 + 11; |
(3.28) |
acd = 8 + 12.
" " ! (3.28) #' 2' ' %-
" ", " " ') . * !
" " $ & % %
') :
0 = d; a1 = c; a2 = b; a3 = a. |
(3.29) |
(3.27) " " ! # (3.28):
F1 = ( 2 + 3 + 6 + 7 ) × f + ( 8 + 12 )× e + ( 12 + 13 + 14 + 15 ) ( e + g ) +
+ 3 + 7 + 11 + 15 + ( 1 + 3 + 9 + 11 ) × l.
* " !, ## # & ) #.
!, # " , % " -
", #) + " ! - !,
+ «"». 3 & ) # " ! #
# " , " % " -
", ') # & 2' " ! "$.
$ ) # ') $') " ! % F1:
F1 = ( 2 + 6 |
) × f + 8 × e + ( 13 + 14 |
) ( e + g ) + |
(3.30) |
|
+ 3 + |
7 + 11 + x12 + 15 + ( 1 + 9 ) × l |
|||
|
||||
" & " # % F2. 4 % -
! " " $ MS-3 &-
% {h, v, w}, + * " " ! # -
" & % " " $
$& #. # * & $# ') .3.16, .
|
|
|
|
|
|
|
|
|
|
w = 4; h w = 1 + 3; h v = 1 + 3; v = 2 + 3 + 6 + 7. |
(3.31) |
||||
hv |
|||||||
* " ') ! & %
" " $ MS-3:
|
|
|
|
|
0 = w, a1 = v, a2 = h. |
(3.32) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 = hv w( k |
+ |
|
|
|
) + h v + h w + vt = x4 ( k + |
|
) + x1 + |
|
|||||||||
r |
r |
|
|||||||||||||||
+ x2 + x3 + ( x2 + x3 + x6 + x7 )× t |
|
||||||||||||||||
) # |
|
||||||||||||||||
|
|
+ |
|
) + x1 + x2 + x3 + ( x6 + x7 )× t . |
|
||||||||||||
F2 = x4 ( k |
(3.33) |
||||||||||||||||
r |
|||||||||||||||||
" ! # (3.30), (3.33) (3.24) ! $ %$' . & " $ -
138

3-& 4-& # ' # & * " , 6
-5. 1 $# 155.
" ! (3.24), & { --5}:
|
|
|
|
|
|
|
|
|
|
|
|
F1 × F2 + mn |
= F1 × |
|
|
|
|
|
|
||
Z = F1·F2 + mn = |
F2 × mn . |
(3.34) |
||||||||
" ! !$ F1 × F2 ! $ -
" $ - + & # " "-
, + ) # # ')-
% F2. ( & " ! ' (3.34) $
' # & * 2 --5. ' $ '
% F2 ! $ " $ -
$& # " ". $ " ! # (3.30) (3.33) + $ * --5:
F1 = ( 2 + 6 ) × f + 8 × e + ( 13 + 14 ) × eg + 3 + 7 + 11 +
+ x12 + 15 + ( 1 + 9 ) × l
F2 = x4 × |
kr |
+ x1 + x2 + x3 + ( x6 + x7 ) × t . |
(3.35) |
" ! # (3.35) $ $') ! -
" ! (3.34) # %$ "
& . # # " )$
& & (&) #
( . " ! # (3.34) (3.35)) . 0 " # # - ') .
1.5 $') & " ! %
" i # - , ')
% " " $ $ &, "- " !. ( ! ! $# «#» #
& " !.
') % " $ " & ",
') * & " !.
2.6 & # (2' #) % " " -
$ ' (2 ') ') - % " $ .
3.( " % " " '-
') % " $ . &.1.
4. 5 $') " ! ' " - " i, * , ') % " " $-
'$ . &.0.
, &$ &" , ) -
+ & ' !&, (, ( !%! %-
139
" !. 5 ! " " ,
!.
' % ' + & ' ! $
. * 91 -
') % " $ 0 !- 6 ,. % " " 93 '$ .-
&.0, % " " 94 '$
. &.1.
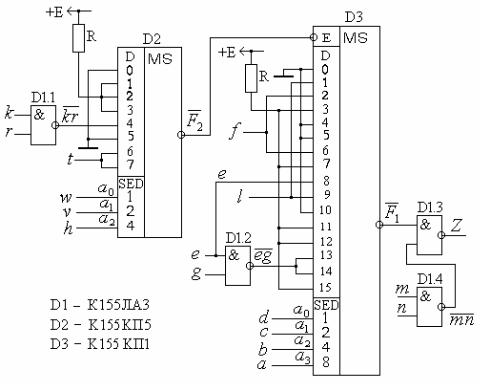
" $ MS-4 MS-3, ,
" 155 1 155 5. & + ! " -
& %$' .3.17.
' # % " $ D2 D3 -
". + " , # -
$ % F1 F2, " " " " $
"!
.3.17. $# $
$ - ( 3-4)
,
$ . 0 # + # (3.32) # $ MS-3 (3.29) # $ MS-4 &
! # * !
140
