
Собакин Е.Л. Цифровая схемотехника (УП)
.pdf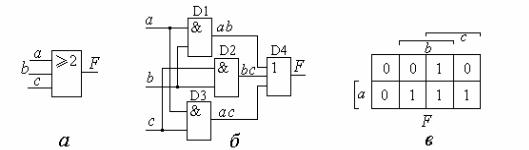
& #') v1 =0 v2 =1 " X
mod2 $ % " &. !
# " Y # * ". - &, " , # & #')
0-0 1-1 " # « » #, &
" & " ' " # -
" % " &.
1.3.11. 6 % ,-* /, ! %
0 * " " ' # & % #, "
& $. # # # ". ( ' & - ! & * & ". " & -
, & '
" #. * * # «!
» + &.
, " " & &
# $ &.1. & ! & * «³ 2 3- » ( #
) & " &.1, (' ")
" & ' &.1.
- .1.12 " 8, & *, " % %$# & * # .
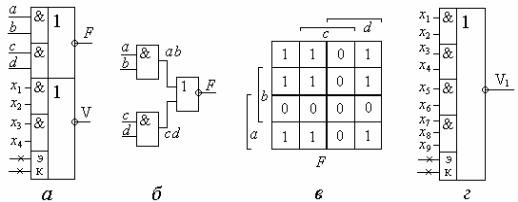
. 1.12. ! " * «³2 3- »: 8, ( ); %-
$# ( ); " % ( )
% F ! + $' 2' '
$' % ( - ):
F = ab + bc + ac. |
(1.16) |
0 % " # .1.12, .
( .1.12, ), " # , ! " - # " + &. & !
$ # ! & * «³3 5- », -
$ & " ! & " %, -
$ %$' .
41
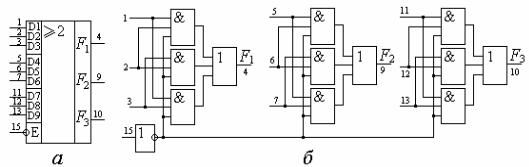
&$ ! " * " $,
#. - , 1533 $ 153363, - #') # ! " * «³2 3- » " )
#. ( & &.0 # . "-
% !, & &.1 ) '.
$# * " + 8, " .1.13.
( ## %$' .1.13, ! & * .1.12, , ! #$, & ,
# ' " " & " #')
( 8, «5») & &.1. (- 8,
.1.13, % " ' " ".)
.1.13. 153363: 8, ( ); %$# ( )
5$ ! " * " " ", , -
" 53363 13463 ! *. *
« $.» $ & &
# (& &.0). ( ! $, ! " *-
, * --5 6--5, " & ",. . # " & ) & #.
1.3.12. 8, ! % «,-* - (- » /, ! % «,0* 0. »
( & " & * ! "$ & *, " " & $
#, & + " & !
' . * " # "$ *-
«& & &». , -
.1, & " & -
&.1, * " " ' * «' ')
6». 0 ! * " & & &, $ «&» -. # 8,( ! & 8,, -
42
& ) # «=1» (# * 6),
«=n», & n $. & & *.
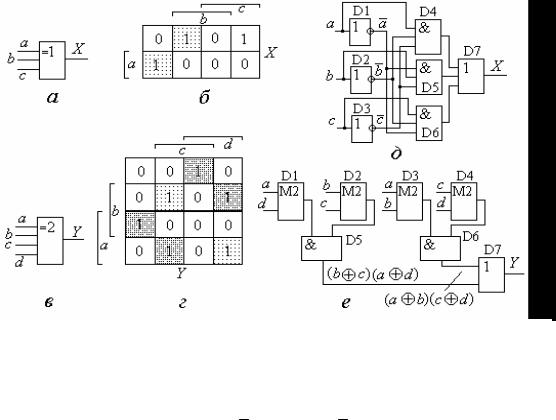
, .1.14 " 8, * 6 #
, 8, * & & & «=2 4- », " "-
" % %$" * " ".
3 # + " " % X Y, ,
$" 2' " & % * % (
$ - & % -
!). * %$" " " * !
$, # & " ! # (- & %.
. 1.14. 6 & * " «' ') 6» & & «=2 4- »: 8, ( , ); " " " % ( , ); %$" *- " " ( , )
, .1.14, ') " ! ': |
|
X = ab c + abc + ab c . |
(1.17) |
0 (- % «' ') 6». 5 " & $ " ! % Y, # " 6 2' " ( - & "), ! " " # " 4- &-
. & %$# * & & & «=2 4- »
# " * 66, . & * 4 4- * -5. ( ! .1.14, ') &
" ! ':
Y = (aÅd)(bÅc) + (aÅb)(cÅd). |
(1.18) |
, # & & " ! - " & % $ !. ( ! -
43
$, mod2 ! # . "
! # . , " ! (1.18)
" " «" . " » ( .1.14, ) # % Y " ) !-
. 3 & " ! ! " " $ # % « - ' ') 6» .1.14, .
( $, , & * «' ') 6» , * % # ! %-
! # mod2 & (2Å). ! ', &$-
& * " «' ') 6» «& &
&» " ' #.
1.3.13. -* /, ! % «# 9 »
0 & * " " ' # % |
«#» |
|||||||
( .1.3 % V11 V14). |
|
|||||||
V11 = b ® a = a + |
b |
= |
a b |
, |
|
|||
|
|
|
|
|
||||
V14 = a ® b = a + b = a |
|
|
. |
|
||||
b |
(1.19) |
|||||||
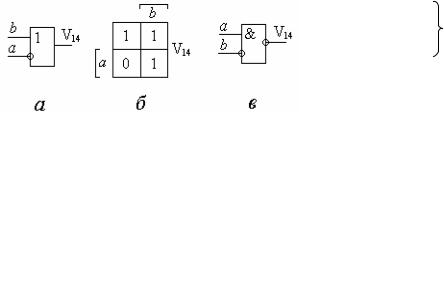
# % " # «# b», # - «#
». - .1.15 " " & % # & & * 6 3 , & " %. "
" ! (1.19) $' , % #
! # # # # % 43 5.
" .1.15, ,
|
! ! $ |
|
, & &- |
|
- |
|
, & - . |
|
&$ |
|
6 3 , = # ( |
|
|
.1.15. 6 & * « - |
. & # |
»: 8, & . # !$- |
" ' #. , - |
& ( ); % ( ); |
& 8, .1.15, , %- |
8, & . # $ - |
' ! - |
& ( ) |
$ * 26, &- |
|
& |
, - * 43 5, ' & " . 0 %$" * " " " , - $-
.
( $, " & * -
, * # " & &
%.
44
1.3.14. -&$, % ,-* /, ! %
". " " « » & * ", "
' " & .
, &$ " ' # ! " & * " (60), " " $ ( , +
. &.0 &.1) $ " %-
. , * * " ' !$ &- " & % % & $" 2' ",
$" 2' " & %. .1.2 ! "
" # &$" %$ '
" #. $ . #- " & %$" 60.
-* /, ! % - -
* " ' " +
( - ) & " ! %, *
+ ( - ) * %. , .1.16
" 8, 15561 15563. 15561 -
! # * 2-2 -26--5, 15563 #
* 2-2-2-3 -46--5, . # " 6.
.1.16. 6 & * " -6--5: 8, " 15561 ( ); %$# * # * 2-2 -26--5 ( );
" % * 2-2 -26--5 ( ); 8, " 15563 ( )
%$ ( .1.16, ) & * "
15561 ! $ ') & " ! & "-
%:
|
|
= (a + |
|
)( |
|
|
|
|
|
|
F = |
ab + cd |
b |
+ d |
) . |
(1.20) |
|||||
c |
||||||||||
45
, * % # 4- &, + # $ "- ! # (1.20) $ 2' $
% % F ( - ). 6 # $ * & " ! #
8, * 2-2 -26--5. ! * *
" «&» " . # 6. , - " $ 8, «*» − * " « » −
". 0 " (" " ") #
"$ , " & " & $ # -
#! #. " " ' # 8, & *-
( ) $" « » ×.
, " ( * " " " "
* % ) #') & & & & * ( 6. ' # " " ') ( «. 6», ! )$ * 6- -5, #) & & %$& *. - , #
" *%% 2 # 8,
. 6 ' & $ - " &. ) . 6 # #' # & "
* .$ , " " & " ' -
" &.0 &.1. , # $ &
" ! (1.20) & " ! " % V # - & *:
V = |
x1 x2 + x3 x4 + |
. |
(1.21) |
$ ') & " " ! (1.21) ! "$ " 8 ( *%% 2 # ),
! & ! "$ ! 2' $
$ &. , " ! # (1.20) (1.21) #'
&-' $ " 15561.
& #$ &-' $
" 15563, $# # * & .1.16, + -
& % .
-* /, ! % -
0 & * " ' % & " 2' " -
$" % ( - ) " %, $ &
& $ &. - , " " -
* 2-26-2 . * " # %
X = (a + b)(c + d). |
(1.22) |
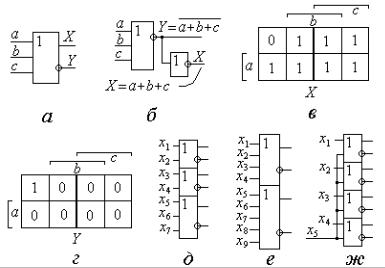
- .1.17 8, * & *, & " % X %$# * # .
&$ " ' # " 60, , -
( 0(6 $ 5006(118, #') # -
46

& * 2-36-2 ) . - .1.17, -
8, * ". + & % '
! $ ') & " ! # " " % Y Z:
Y = (x1 + x2 + x3)(x4 + x5 + x6), |
(1.23) |
Z = (x6 + x7 + x8)(x9 + x10 +x11). |
|
" ! # (1.23) # #' # &- $' -
". - ) & x6 + !$ $-
$ 5006(118 " *
2-36-2 ( x6=0),
.1.17. 6 & * " 6- : 8, * 2-26-2 ( ) & %$# * # ( ); & " % ( ); 8, " 5006(118 ( )
" * 36 ( x6 =1). * &
$#, ') # x6 " ! # (1.23).
-* /, ! % - /
), * * " # #' # * 6 # "-
− # " ". * ' 2'- ' ' 2' & & ! ! " &-
" ' # + " & % #.
.1.18, 8, * 36--5 / 36 " & %
# 500, ! ) " & *-
". - ! " " " " % -
& *, %$# * # & ( .1.18, )
8, 5006105 ( .18, ), 5006109 ( .1.18, )
5006101 ( .1.18, ). ( $, + " %-
$ " " − * 36--5 ! "$
$ * 36 ! * -5. " & %
# " #$, (
47
5006105 ! " *: * 26--5/
26 * 36--5 /36.
3 & ! #$ " 5006109 ( .1.18, ). , 8, " 5006101( .1.18, ). -
! 4 " * 26--5 /26 $- " " ) 5. 5 & * 5 = 0, ! $ 4- * -5 ,
! #, " + & 1,
2, 3 4. 5 ! 5 = 1,
&
" &
# " " -
# # & " &.1, "
" & " &.0. , ! " *
&
$ -
-
|
. |
|
. 1.18. 0 " 6--5 /6: 8, * 36- |
$ |
|
, |
||
-5 /36 ( ) & %$# ( ); " |
||
" " % X Y ( , ); 8, |
500 ' # &- |
|
5006105 ( ), 5006109 ( ), 5006101 ( ) |
* " |
|
|
6- --5/6- , |
5006117. 0 − , & "
5006(118 ( .1.17, ) , ! " * 2-26-2
# " " ".
" . $"
% " & * ". 3 # ! " -, ! ') ":
1.( ) -
60 & !-
* & .
2.( ) .*& *
& ! .
* % * " # & " !- # & %, " *.
3.$" " ! " 60 ! $
" ( ! ") , + )
48

(&$) # %$" *-
" # & & ! 60.
$ & ) #' -
$ # " & *, % " % "% ! $ & '.
( , !, - ! ( & ' ! ! , %! , * ! 60 * ! ! ,-
' ! , & %. & , $ !-
! , %! (( & %! ) !.
1 * ( , !% " # &$,
( , % ,-* /, ! " -
.
1.3.15.&$, ( , % % ,-* /, !
' ! " # 60, " ( -
") ! $ !
" ". &$, ( , & & *-
, ' $, # # ( , ' !% ,-* -
&$', " # #' # &- # "-
& 60.
& ) 1-2, & -
' #
!. ( )$ * " # ').
-# & % , -
!:
) % ', 0, f (x1, x2, ¼xn) = f (0, 0, ¼0) ¹ 0;
) % ', 1, f (x1, x2, ¼xn) = f (1, 1, ¼1) ¹ 1;
) % ', ,
f (x1, x2 , xn ) ¹ f (x1, x2 , xn ) ;
&) % ', ,
f (x1, x2, ¼xn) ¹ 1 Å 2 Å ¼Å n Å 1 2 Å ¼ Å 1 2¼xn;
) % ', .
5 :1 $ " % " &
% f (x1,x2,x3,x4), :1 = <x1, x2, x3, x4> = <1,1,0,1>, :2 = <x1, x2, x3, x4> = <0,0,0,1> - & * &, ! $, :1
> :2, . . :2 $. :1.
49
5 % f (:1) < f (:2), . . % $-
. $. + ! # $. &, %-
# .
, ' & $ #$ %, ! # - " " . &, $ -
« » ! !, #$' -
. 3 &, ! "$ , + " +
%.
5 # & % # -
+ # " %, ' " '
) !, %, ') +, " ' ) %! &$!.
& , ! $ & %. ' $, ! $ # % #,
% . . * " # # « $"», «"- "» , # * , %,
% . " ".
$# ' %, ! "-
$ ( $) !. & & ($( &( ( )$ , & &-
% ! #$ & % ( "
") $ ! " %.
3 & " # # ! $ $ $ !
& *. 0 , ')
" !, &$,
( , !& & ,-* /, ! . ! -
$ & . 0 ", ')
%$ " , " ' # ) %! ,-* ! /, -
! !.
, ! & % & ( . 1.3) " " $" .
, ", & % & % # #-
# (- (- , - , - . * & % #' # 2', 2' -
, 60, #) * , 6 -5. 0 # # # . * & #, #
# $ { , 6, -5}.
, !
& & *, ') # #! $-
#-). , !-
60 (& &) # # # -
$ &, , #$ $ #)
*, ! − + !, + ! -
.
50
