Энтропия. Теорема Карно

Кроме термодинамических параметров p, V, T и функции состояния системы - внутренней энергии U, в термодинамике используются и другие функции состояния системы. Особое место среди них занимает энтропия. Как это следует из теоремы Клаузиуса, для любого бесконечно малого обратимого процесса отношение dQ/T есть полный дифференциал некоторой функции состояния системы, которая называется энтропией.

dS =  dQ/T.

Для любого конечного процесса интеграл вида:

S₂ - S₁  = dQ/T ,

выражает изменение энтропии.

Каждому состоянию системы соответствует определенное значение энтропии S (подобно внутренней энергии U). Энтропия системы как целого равна сумме энтропий отдельных частей системы, т.е. энтропия аддитивная величина. Как видно из определения энтропии, можно рассчитать только ее изменение, а не саму энтропию. Однако для термодинамики, изучающей в основном различные процессы в веществе, этого вполне достаточно. В расчетные формулы при описании различных процессов будет входить изменение энтропии. То же самое можно сказать и о внутренней энергии. dS и dQ имеют одинаковые знаки. Это позволяет судить о направлении теплообмена по изменению энтропии. Например, при нагревании тела ( dQ > 0) его энтропия возрастает. При адиабатном процессе ( dQ = 0) энтропия системы не изменяется. Весьма полезно многие процессы изображать на диаграмме в координатах T - S (T - S диаграммы). Рассмотрим любой обратимый процесс в координатах T - S (рис. 8).

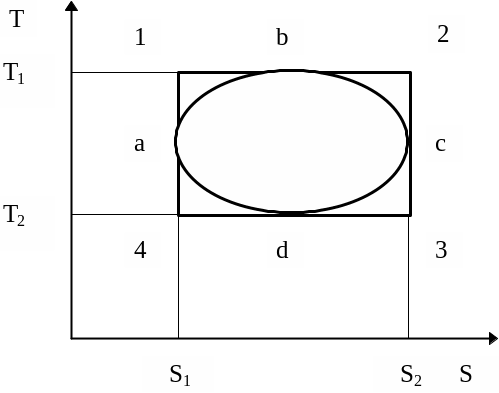
Рис. 8. Теорема Карно и максимальный КПД тепловой машины

Из определения энтропии следует, что для обратимого процесса dQ = TdS. Количество теплоты, сообщенное системе в процессе 12, будет равно площади всей фигуры S₁12S₂:

Q₁₂ = dQ = TdS.

Используя T - S диаграмму можно доказать теорему Карно: к.п.д. цикла Карно максимален и не зависит от природы рабочего тела и конструкции идеальной тепловой машины, а определяется только температурами нагревателя и холодильника.

Рассмотрим любой произвольный обратимый круговой процесс аbсdа. Как видно из диаграммы, к рабочему телу в процессе abc подводится тепло Q₁ = TdS > 0. В процессе cda отводится Q₂’= - Q₂ =  TdS < 0. Работа за весь цикл A соответствует площади, ограниченной замкнутой кривой abcda. По определению  h_обр = A/Q₁ . В частности для цикла Карно (рис. 8):

h_K = (T₁ -T₂ )(S₂ -S₁ )/[T₁ (S₂ - S₁ )] = (T₁ -  T₂ )/T₁ ,

без каких либо ограничений на тип рабочего тела и идеальной тепловой машины. Полученная формула совпадает с формулой, полученной ранее в предположении, что рабочим телом является идеальный газ.

Из диаграммы для произвольного обратимого цикла видно, что

Q₁  = T₁(S₂ - S₁) - (A₁ +A₂), а Q₂ = T₂(S₂ - S₁) + (A₃ + A₄). Тогда h_обр = (Q₁ - Q₂)/Q₁ =

= [T₁(S₂ - S₁) - (A₁ +A₂) - T₂(S₂ - S₁) - (A₃ + A₄)]/ [T₁(S₂ - S₁) - (A₁ +A₂)] =

= [T₁(S₂ - S₁) - T₂(S₂ - S₁) - (A₁ +A₂ + A₃ +A₄)]/[T₁(S₂ - S₁) - (A₁ +A₂)], или

h_обр = ,

где - k = (A₁+A₂ + A₃ +A₄)/[(T₁ - Т₂)(S₂ - S₁), k’= (A₁+A₂) )/[(T₁ - Т₂)(S₂ - S₁).

Очевидно, что k >k’. Тогда (1-k)/(1-k’) < 1, что доказывает максимальность КПД цикла Карно по сравнению с другими циклами (h_обр £ h_К).