Уравнение плоской синусоидальной волны

Несмотря на большое разнообразие физических процессов, вызывающих волны, образование волн и их распространение происходит по одному общему типу и описывается одинаковыми уравнениями.

Пусть в направлении оси ОХ распространяется плоская волна, полученная от источника волн, в котором изменения колеблющейся величины происходит по закону

с амплитудой А, циклической частотой  и начальной фазой ₀. Совместим положение источника волн с началом координат (рис.). Если пренебречь затуханием волны, то колебания частиц в точке, отстоящей на расстоянии Х от источника, будут происходить тоже по закону (74), но с опаздыванием по времени на величину

_{ЗАП =} ,

где V - скорость распространения фронта волны. Поэтому смещение S физической величины от положения равновесия в точках, находящихся на расстоянии Х от источника в момент времени t, является уже функцией двух переменных Х и t:

Уравнение называется у р а в н е н и е м п л о с к о й с и н у с о и д а л ь н о й в о л н ы, распространяющейся вдоль оси ОХ.

Д л и н о й в о л н ы  называется расстояние, пройденное фронтом волны за период колебаний источника волн

=VT= = .

Величина

называется в о л н о в ы м ч и с л о м и показывает, сколько длин волн укладывается на расстоянии, равном 2 единиц длины. С учетом уравнение будет иметь вид

На рис. представлена как бы «мгновенная фотография» плоской поперечной синусоидальной волны с длиной волны  и начальной фазой ₀=0.

При переходе волны из одной среды в другую частота ее =/2 не меняется, пока источник волн работает по закону. Но длина волны  будет меняться, так как изменяются свойства среды. Поэтому скорость волны тоже будет меняться, в одной среде V₁=₁ , в другой V₂=₂ .

При распространении плоской волны вдоль произвольного направления r

,

где - в о л н о в о й в е к т о р, по модулю равный волновому числу к и направленный вдоль луча в рассматриваемой точке среды, характеризующейся радиус-вектором .

Учитывая (1а), уравнение (80) можно записать в экспоненциальной форме, удобной для дифференцирования:

.

Уравнение синусоидальной сферической волны имеет вид

,

где А/r - амплитуда сферической волны, убывающая обратно пропорционально расстоянию фронта волны от источника колебаний r. Это происходит потому, что энергия, переносимая сферической волной за единицу времени через любую сферическую поверхность, должна быть одна и та же и равна энергии, расходуемой источником за это же время

( а так как ~ , то ~ ).

П л о с к а я с к а л я р н а я волна произвольного вида, распространяющаяся вдоль оси ОХ со скоростью V, имеет вид

.

Предположим теперь, что некоторая векторная величина (скорость, напряженность электрического и магнитного поля и так далее) является функцией координат и времени

В этом случае говорят о п л о с к о й в е к т о р н о й волне, распространяющейся вдоль оси ОХ со скоростью V. Если вектор перпендикулярен к направлению распространения волны, то векторная волна называется п о п е р е ч н о й, если вектор параллелен направлению распространения волны, то волна будет п р о д о л ь н о й.

Волновое уравнение

Уравнение для любой волны вида являются решениями дифференциального уравнения, называемого в о л н о в ы м. Установим вид волнового уравнения для плоской волны произвольного вида. Для этого сопоставим вторые частные производные по х и t:

; ;

; .

Из соотношений следует

.

Это дифференциальное уравнение в частных производных второго порядка, которое называется в о л н о в ы м у р а в н е н и е м. Любая функция, удовлетворяющая этому уравнению, будет описывать плоскую волну, распространяющуюся со скоростью V в направлении оси ОХ.

Распространение волн в трех измерениях в однородной не поглощающей среде описывается волновым уравнением

или  ,

где = - оператор Лапласа.

Для векторной волны волновое уравнение имеет вид

 .

Волны различной природы

Упругие волны в твердом теле

Рассмотрим упругую волну в тонком упругом твердом стержне (рис.). Пусть частицы стержня с координатой x₁ в момент времени t испытывают относительную деформацию сжатия ,

частицы с координатой x₂ в этот же момент времени - . Результирующая сила F, действующая на элемент объема V=S₀x , при условии выполнения закона Гука

;  ,

где Е - модуль Юнга вещества стержня. По второму закону Ньютона

,

где - плотность вещества стержня. При х 0 с учетом того, что ускорение :

;

согласно скорость фронта продольной волны в стержне

V _ = ,

Таким же образом можно показать, что скорость поперечных волн, обусловленных распространением упругой деформацией сдвига, в неограниченной твердой среде

V_ = ,

где G - модуль сдвига среды, а  - ее плотность.

Скорость поперечных волн в натянутой струне зависит от силы натяжения струны

,

Энергия волны

При распространении волн происходит перенос энергии без переноса вещества. В силу того, что энергия волны распределена в пространстве неравномерно, имеет смысл говорить о плотности энергии.

Упругая среда, в которой распространяются м е х а н и ч е с к и е в о л н ы, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией среды.

Рассмотрим плоскую продольную упругую волну в тонком стержне S(x,t)=f(1-x/V) . Объемная плотность кинетической энергии определяется следующим равенством:

,

где dK - кинетическая энергия всех частиц в бесконечно малом объеме dv стержня, выбранном так, что в его пределах скорость частиц среды U(x,t)= одинакова; - плотность среды.

Объемная плотность потенциальной энергии

,

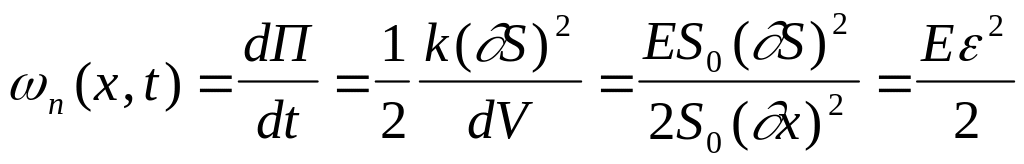где dП - потенциальная энергия однородно деформированного малого участка среды объемом dV=S₀dx;

k - малого участка стержня длиной dx и сечением S₀ , прямо пропорциональная произведению (ES₀) и обратно пропорциональная длине этого участка;

- относительная деформация рассматриваемого участка.

Учитывая выражение (99) и равенство ,получим

.

Таким образом, плотности кинетической и потенциальной энергий упругой волны равны между собой в любой момент времени в любой точке среды. Следует отметить, что в отличие от локализованных колебаний осциллятора, где кинетическая и потенциальная энергии изменяются в противофазе (см. (12) и (13)), в бегущей волне колебания кинетической и потенциальной энергий происходят в одинаковой фазе.

Плотность полной энергии упругой волны

.

Из равенства (114) следует, что энергия бегущей волны перемещается вместе с волной с той же скоростью V без переноса частиц среды, колеблющихся около своих положений равновесия. При этом,

согласно закону сохранения энергии, должна уменьшаться энергия источника волн. Для синусоидальной волны (79)

;

.

Вектором плотности потока энергии (вектором Умова) называется вектор, направленный в сторону переноса энергии волны и равный по величине отношению энергии, переносимой волной за единицу времени сквозь малую площадку dS к площади dS_ - проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии. Так как энергия dE_мех заключена в элементе объема

, то

;

.

Скалярная величина I , равная модулю среднего значения вектора Умова, называется и н т е н с и в н о с т ь ю в о л н ы :

.

Для синусоидальной волны

.