Лабораторная работа № 13

ПОСТРОЕНИЕ И АНАЛИЗ ДИАГРАММ «СОСТАВ–СВОЙСТВО»

Цель работы – освоить методику получения полиномиальных моделей для описания зависимости свойства от состава смеси и диаграмм «Состав–свойство»; определить оптимальное состав смеси (композиции)

Краткие теоретические сведения

В химической технологии часто приходится решать задачи поиска оптимального соотношения компонентов исходных смесей для получения материала с заданными свойствами. Поскольку требования, предъявляемые к материалам, различны, число возможных вариантов соотношений компонентов, удовлетворяющих этим требованиям, может быть велико.

При изучении свойств смеси, зави­сящих только от соотношений компонентов, используют метод симплекс планирования. При данном методе факторное пространство (пространство координаты которого соответствуют рассматриваемым факторам) представляет собой правильный (q–1)-мерный симплекс – простейший выпуклый многогранник, вершины которого равноудалены от центра фигуры. Для таких систем переменные не являются независимыми и выполняется соотношение

где х_i – концентрация компонента системы, i=1,2…q; q – количество компонентов.

Для двухкомпонентных систем симплекс – прямая, а содержание компо­нентов определяется соотношением отрезков. При q=3 правильный симплекс – равносторонний треугольник. Каждая точка треугольника от­вечает одному определенному составу тройной системы и, наоборот каждый состав представляется одной определенной точкой. Состав мо­жет быть выражен в мольных, весовых или объемных долях или про­центах.

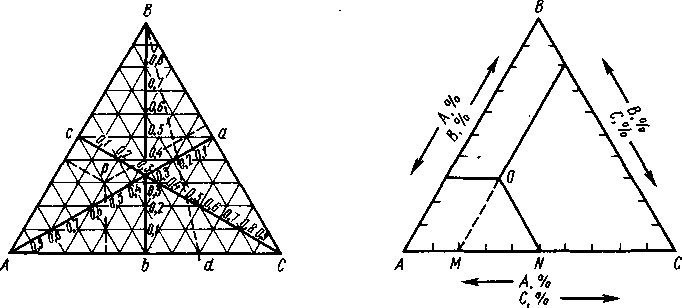
Рисунок 1 – Концентрационный треугольник Гиббса

Рисунок 2 – Концентрационный треугольник Розебума

Вершины треугольника соответствуют чистым веществам, сто­роны – двойным системам. Опустив из каждой вершины треугольника высоту, разделив каждую из них на десять равных по величине отрезков и проведя через полученные деления прямые, параллельные сторонам треугольника, получим треугольную сетку. Приближение от каждой дан­ной стороны к противоположной вершине отвечает пропорциональному возрастанию содержания соответствующего компонента, поэтому пря­мые, параллельные данной стороне, при последовательном переходе от одной прямой к другой отражают возрастание третьего компонента на 10 %. На рисунке 1 на соответствующих высотах треугольника указано содержание каждого из компонентов (в точке d—30% А и 70% С). Практи­чески большей частью не прибегают к построению высот, можно откладывать содержание компонентов непосредственно на сторонах треугольника. Такой способ отсчета принят в треугольнике Гиббса.

В треугольнике Розебума состав тройной системы отсчитывается по трем отрезкам одной стороны треугольника (рисунок 2). В концентрацион­ном треугольнике точки, лежащие на прямой, выходящей из вершины треугольника, соответствуют смесям с постоянным отношением содер­жаний компонентов, изображаемых двумя другими вершинами.

Свойство (Y) обычно представляют проекциями линий равного значения (изолиниями) на плос­кость концентрационного треугольника.

При q=4 правильный симплекс – тетраэдр, каждая вершина которого соответствует чистым компонентам. Ребро представляет собой двухкомпонентную систему, грань – трехкомпонентную. Точки внутри тет­раэдра соответствуют четырехкомпонентным системам. Так, компонент x₁, отсутствует на грани x₂, x₃, x₄, а по сечениям тетраэдра, приближаю­щимся к вершине x₁, содержание компонента x₁, увеличивается.

Графически такую систему представляют в виде сечений трехмерного симплекса плоскостями, перпендикулярными одной из его осей. Состав четырехкомпонентных смесей, лежащих в плоскости сечения, опреде­ляется уже двумерным симплексом, что позволяет изменение свойств системы представлять в виде контурных кривых. При этом в одном сечении варьируют только тремя компонентами. Переход от одного сечения к другому соответствует изменению четвертого компонента.

При планировании эксперимента для решения задач на диаграммах состав – свойство предполагается, что изучаемое свойство является непрерывной функцией аргументов и может быть с достаточной точ­ностью представлено полиномом.

Использование методов планирования эксперимента позволяет значительно сократить объем эксперимента при изучении многокомпонентных систем, отпадает необходимость в пространственном представлении сложных поверхностей, так как свой­ства можно определять из уравнений. При этом сохраняется возмож­ность графической интерпретации результатов.

В настоящее время наибольшее применение получили симплекс-решетчатые планы, предложенные Шеффе, позволяющие при малом количестве опытов получить для описания влияния соотношения компонентов на свойства продукции уравнения 1-го, 2-го и более высоких порядков. Экспериментальные точки рас­полагаются в узлах сетчатой структуры в барицентрической системе координат и представляют {q, n}-решетку на симплексе, где q – число компонентов смеси; n – степень полинома. Некоторые {3, n}-решетки представлены на рисунке 3, а {4, n} – на рисунке 4.

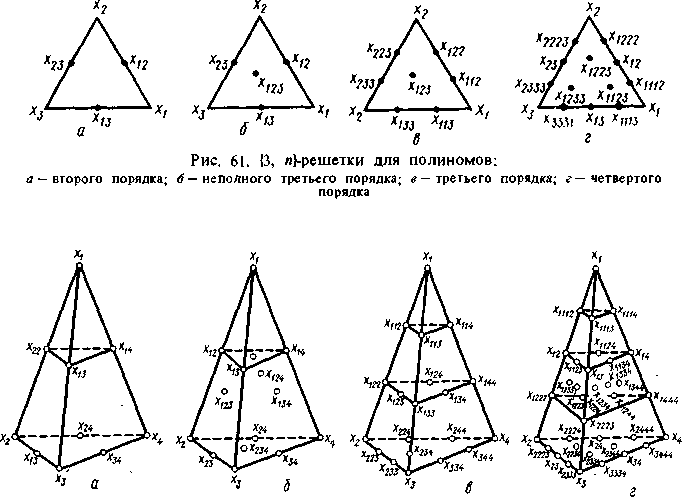
Рисунок 3 – {3, n}-решетки для полиномов: а) – второго порядка; б) неполного третьего порядка; в) третьего порядка; г) – четвертого порядка

Рисунок 4 – {4, n}-решетки для полиномов: а) – второго порядка; б) неполного третьего порядка; в) третьего порядка; г) – четвертого порядка

Планы на симплексных решетках, т.е. планы Шеффе, не обладают обычно свойством композиционности, т.е. для перехода к построению более сложной модели исследователю приходится ставить новые опыты, не полностью используя информацию, полученную из предыдущих опытов.

Записав координаты точек симплексной решетки, получают матрицу планирования. В таблице 1 приведена матрица планирования для построения полинома четвертой степени в трехкомпонентной системе. Индексы у свойства смеси указывают на относительное содержание каждого компонента в смеси.

Коэффициенты приведенных полиномов получают, используя свойство насыщенности плана. Для получения коэффициентов полинома последовательно подставляют в уравнение координаты всех точек матрицы планирования.

Так, например, для полинома четвертой степени, выраженного уравнением:

у = β₁·X₁ + β₂·X₂ + β₃·X₃ + β₁₂·X₁·X₂ + β₁₃·X₁·X₃ + β₂₃·X₂·X₃ + γ₁₂·X₁·X₂·(X₁–X₂)+

+ γ₁₃·X₁·X₃·(X₁–X₃) + γ₂₃·X₂·X₃·(X₂–X₃) + δ₁₂·X₁·X₂·(X₁–X₂)²+ δ₁₃·X₁·X₃·(X₁–X₃)²+

+ δ₂₃·X₂·X₃·(X₂–X₃)² + β₁₁₂₃·X²₁·X₂·X₃ + β₁₂₂₃·X₁·X²₂·X₃ + β₁₂₃₃·X₁·X₂·X²₃,

Таблица 1 – Матрица планирования

№ опыта	х1	х2	х3	у
1	1,00	0,00	0,00	у1
2	0,00	1,00	0,00	у2
3	0,00	0,00	1,00	у3
4	0,50	0,50	0,00	у12
5	0,50	0,00	0,50	у13
6	0,50	0,50	0,50	у23
7	0,00	0,25	0,00	у1112
8	0,75	0,75	0,00	у1222
9	0,35	0,00	0,25	у1113
10	0,75	0,00	0,75	у1333
11	0,25	0,75	0,25	у2223
12	0,00	0,25	0,75	у2333
13	0,50	0,25	0,25	у1123
14	0,25	0,50	0,25	у1223
15	0,25	0,25	0,50	у1233

коэффициенты могут быть рассчитаны согласно следующим уравнениям:

₁ = y₁ и т.д.

₁₂ = 4y₁₂ - 2y₁ - 2y₂;

₁₃ = 4y₁₃ - 2y₁ - 2y₃;

₂₃ = 4y₂₃ - 2y₂ - 2y₃;

₁₂ = 8/3 (-y₁ + 2y₁₁₁₂ - 2y₁₂₂₂ + y₂);

₁₃ = 8/3 (-y₁ + 2y₁₁₁₃ - 2y₁₃₃₃ + y₃);

₂₃ = 8/3 (-y₂ + 2y₂₂₂₃ - 2y₂₃₃₃ + y₃);

₁₂ = 8/3 (-y₁ + 4y₁₁₁₂ - 6y₁₂ + 4y₁₂₂₂ - y₂);

₁₃ = 8/3 (-y₁ + 4y₁₁₁₃ - 6y₁₃ + 4y₁₃₃₃ - y₃);

₂₃ = 8/3 (-y₂ + 4y₂₂₂₃ - 6y₂₃ + 4y₂₃₃₃ - y₃);

₁₁₂₃ = 32(3y₁₁₂₃ - y₁₂₂₃ - y₁₂₃₃) + 8/3(6y₁ - y₂ - y₃) - 16(y₁₂ + y₁₃) - 16/3(5y₁₁₁₂ + 5y₁₁₁₃ - 3y₁₂₂₂ - 3y₁₃₃₃ - y₂₂₂₃ - y₂₃₃₃);

₁₂₂₃ = 32(3y₁₂₂₃ - y₁₁₂₃ - y₁₂₃₃) + 8/3(6y₂ - y₁ - y₃) - 16(y₁₂ + y₁₃) - 16/3(5y₁₂₂₂ + 5y₂₂₂₃ - 3y₁₁₁₂ - 3y₂₃₃₃ - y₁₁₁₃ - y₁₃₃₃);

₁₂₃₃ = 32(3y₁₂₃₃ - y₁₁₂₃ - y₁₂₂₃) + 8/3(6y₃ - y₁ - y₂) - 16(y₁₃ + y₂₃) - 16/3(5y₁₃₃₃ + 5y₂₃₃₃ - 3y₁₁₁₃ - 3y₂₂₂₃ - y₁₁₁₂ - y₁₂₂₂).

После определения коэффициентов уравнения регрессии необходимо провести статистический анализ полученных результатов: проверить адекватность уравнения и построить доверительные интервалы значе­ний отклика, предсказываемые по уравнению регрессии. При постанов­ке эксперимента по симплекс-решетчатым планам нет степеней свобо­ды для проверки адекватности уравнения, так как эти планы насыщен­ные. Для проверки адекватности ставят опыты в дополнительных, так называемых контрольных точках. Число контрольных точек и их координаты связаны с постановкой задачи и особенностями экспери­мента. При этом стараются предусмотреть возможность использования контрольных точек для улучшения модели при неадекватности.

Проверку адекватности проводят в каждой контрольной точке. Для этого составляют отношение:

где ; n – число параллельных опытов в каждой точке, ξ – зависит только от состава смеси и определяется согласно соответствующим графикам для полиномов заданного порядка (см. приложение); s_y – среднеквадратичное отклонение, рассчитанное исходя из дисперсии воспроизводимости.

Величина t, распределенная по закону Стьюдента, сравнивается с табличным значением t_α/l,v, которое определяется исходя из числа степеней свободы v (принимается равным числу степеней свободы дисперсии воспроизводимости) и уровню значимости равному α/l – где l число контрольных точек. Гипотеза об адекватности принимается, если t_α/l,v < t_кр.

Для построения доверительного интервала:

где – табличное значение критерия Стьюдента, которое определяется исходя из числа степеней свободы, равному числу степеней свободы дисперсии воспроизводимости и уровня значимости α/m – где m – число коэффициентов в модели. Планирование эксперимента при исследовании локальных участков диаграмм. При изучении диаграмм «состав-свойство» q-компонентных смесей часто возникает необходимость исследовать зависимость свойства от состава не во всей области изменения концентрации компонентов, а в локальном участке диаграммы.

Изучаемая локальная область на диаграмме может представлять собой неправильный симплекс, координаты вершин которого

известны. Чтобы иметь возможность применять в этом случае планы, используемые для изучения полных диаграмм, проводят перенормировку и принимают составы в вершинах A_j, j=1,2, …, q за самостоятельные псевдокомпоненты так, чтобы для всей области локального симплекса выполнялось условие

Планирование экспериментов осуществляется в системе координат псевдокомпонентов. Относительно новых переменных z₁, z₂,…, z_q, удовлетворяющих указанному ранее условию могут быть построены все ранее описанные планы. Для проведения экспериментов необходимо перейти от псевдокомпонентов z_i к исходным компонентам x_i. Для любой u-ой точки плана этот пересчет осуществляется по формуле:

где x_i – содержание i-го компонента в вершине z_j(A_j).

Реализовав план, рассчитывают коэффициенты уравнения регрессии в координатах псевдокомпонентов.

используя формулы для соответствующих планов, и проверяют его адекватность. Для практического использования уравнение регрессии записывают в исходной системе координат при помощи формул перевода координат из одной системы в другую:

Значения находятся при решении (q-1) систем уравнений.

Поскольку перевод координат возможен только для уравнений с независимыми переменными, исходное уравнение регрессии необходимо преобразовать, исключив одну переменную.

Задача. Получить математическую модель в координатах псевдокомпонентов, проверить ее адекватность и построить трехкомпонентную смесевую диаграмму, которая устанавливала бы взаимосвязь между соотношением псевдокомпонентов и кажущейся плотностью  сырых заготовок при неизменных условиях их формирования.

Исходные компоненты: тонкомолотый (менее 1 мкм) нефтяной кокс – x₁; порошок карбида кремния зернистостью (около 100 мкм) – x₂; порошок карбида кремния зернистостью (около 20 мкм) – x₃. Исследовалась частная диаграмма с вершинами (псевдокомпонентами) состава, мас.%; z₁ [(x₁=80); (x₂=10); (x₃=10)]; z₂ [x₁=10); (x₂=80); (x₃=10)]; z₃ [x₁=10); (x₂=10); (x₃=80)]

Был выбран симплекс-план из 15 опытов (см. рисунок 4), позволяющий аппроксимировать поверхность отклика полиномом четвертой степени.

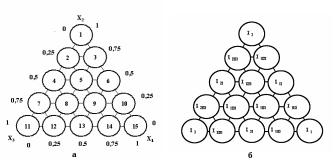
Рисунок 3 – Экспериментальные составы (а) и {3,4}-решетка для построения полинома 4-го порядка (б)

Матрица планирования и результаты эксперимента (в каждой точке делали три параллельных опыта для проверки адекватности модели) приведены в таблице 2.

Таблица 2 – Матрица планирования для диаграммы «Состав–плотность»

№ опыта	Содержание псевдокомпонентов, доли единиц			Плотность, г/см3
	z1	z2	z3
1	1,00	0,00	0,00	у1=1,43
2	0,00	1,00	0,00	у2=2,12
3	0,00	0,00	1,00	у3=1,83
4	0,50	0,50	0,00	у12=1,83
5	0,50	0,00	0,50	у13 =1,67
6	0,00	0,50	0,50	у23=2,08
7	0,75	0,25	0,00	у1112=1,53
8	0,25	0,75	0,00	у1222=2,06
9	0,75	0,00	0,25	у1113=1,52
10	0,25	0,00	0,75	у1333=2,06
11	0,00	0,75	0,25	у2223=2,16
12	0,00	0,25	0,75	у2333=1,92
13	0,50	0,25	0,25	у1123=1,79
14	0,25	0,50	0,25	у1223=1,96
15	0,25	0,25	0,50	у1233=1,87

Для проверки адекватности модели провели два контрольных опыта l=2 в точке с координатами z₁=0,2; z₂=0,33; z₃=0,47; или x₁=24 мас.%; x₂=33,1 мас.%; x₃=42,9 мас.%. Для этого состава согласно треугольникам в приложении ξ=1, уровень значимости α=0,05. Экспериментальные значения кажущейся плотности для проведенных опытов в контрольных точках составили 1,936 и 1,943. Дисперсия воспроизводимости для трех серий параллельных опытов составила при степенях свободы v=38.