
- •1. Что такое эконометрика?
- •1. Что такое эконометрика?
- •2. Основные типы эконометрических моделей
- •2.1. Регрессионные модели с одним уравнением
- •2.2. Модели временных рядов
- •2.3. Системы одновременных уравнений
- •3. Однофакторная парная регрессионная модель
- •3.1. Функциональная спецификация модели
- •3.2. Парная линейная регрессия
- •4. Множественная регрессия
- •4.1. Нахождение оценок неизвестных параметров
- •4.2. Значимость модели множественной регрессии
- •4.3. Мультиколлинеарность
- •4.4. Гетероскедастичность
- •4.5. Автокорреляция
- •4.6 Фиктивные переменные
- •5. Реализация типовых задач на компьютере
- •5.1 Регрессионный анализ в ms Excel
- •5.2 Другие возможности ms Excel
- •5.3 Анализ полученной модели
- •6. Задачи
- •Глоссарий
- •Список вопросов к экзамену (зачету)
4.4. Гетероскедастичность
Для применения МНК необходимо, чтобы дисперсия остатков была гомоскедастичной (3 условие Гаусса - Маркова), то есть дисперсия должна быть постоянной и не зависеть от номера наблюдения (E( )=V( )= – не зависит от j, j=1…n).
В случае, когда это условие не выполняется, то имеет место гетероскедастичность. На практике гетероскедастичность в моделях встречается достаточно часто, что приводит к получению неэффективных оценок регрессии.
При малом размере выборки для оценки гетероскедастичности используют тест Голдфельда – Куандта.
Данный тест можно применять при предположении о прямой зависимости дисперсии ошибки от величины некоторого регрессора (х).
Алгоритм проверки:
1) упорядочить статистические данные (n наблюдений) по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность (х);
2) исключить d средних наблюдений, где (n-d):2>m, m –число регрессоров в модели (для простоты можно взять d=1/4 от общего количества наблюдений);
Замечание: если число наблюдений четное число, то и d должно быть четным. Например, если n=36, то d=n/4=9, в данном случае берем d=10 и делим оставшуюся совокупность данных на две равные группы (36-10) / 2= 13).
3) построить по
двум полученным группам уравнения
регрессии (первая группа: первые n/2–d/2
наблюдения, вторая группа: последние
n/2–d/2
наблюдения),
рассчитать для них остатки e1
и e2,
где
 ;
;
4)
составить статистику
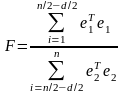 (4.4.1)
(4.4.1)
где
 - транспонированный столбец вектора
ошибок;
- транспонированный столбец вектора
ошибок;
Замечание:
транспонированная матрица
 получается путем замены в исходной
матрице А строк на столбцы.
получается путем замены в исходной
матрице А строк на столбцы.
В MS Excel можно использовать функцию ТРАНСП
5) проверить гипотезу Н0: 12 = 22 = …= n2 о постоянстве дисперсии с помощью критического значения F – статистики Фишера с (n/2–d/2–m, n/2–d/2–m) степенями свободы, которые можно рассчитать в MS Excel c помощью функции FРАСП.
Если
 ,
то гипотеза о гетероскедастичности
подтверждается.
,
то гипотеза о гетероскедастичности
подтверждается.
Если
 ,
то гипотеза о гетероскедастичности
отвергается.
,
то гипотеза о гетероскедастичности
отвергается.
В случае подтверждения гипотезы о гетероскедастичности для поиска оценок коэффициентов регрессии могут применяться следующие методы:
- обобщенный метод наименьших квадратов;
- обычный метод наименьших квадратов, если оценки ошибок представлены в форме Уайта или Невье – Веста.
В случае наличия в модели гетероскедастичности, оценки, полученные МНК, являются неэффективными. Для получения более эффективных оценок применяют следующую процедуру:
1) оценивается исходный ряд методом наименьших квадратов, получаем уравнение регрессии;
2) ряд исследуемых данных условно делится на 2 равные совокупности: первая совокупность от 1 до t, вторая совокупность от t+1 до n;
3) предполагается,
что
 ,
,
 (4.4.2)
(4.4.2)
 ;
;
4) по первым t
наблюдениям вычисляется модельное
значение
,
вычисляется вектор остатков
 ,
за оценку
,
за оценку
 берут
берут
 (4.4.3)
(4.4.3)
где m – число регрессоров в уравнении;
4) аналогично по
последним (n-t)
наблюдениям вычисляется вектор остатков
 ,
за оценку
,
за оценку
 берут
берут
 (4.4.4)
(4.4.4)
5) преобразуем
исходную модель, полученную МНК путем
деления первых t
уравнений на
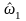 ,
а последних (n-t)
уравнений на
,
а последних (n-t)
уравнений на
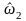 ;
;
6) из полученной модели находим более эффективнее оценки МНК – оценки коэффициентов.
