4. Множественная регрессия

Модель парной регрессии дает хорошие результаты, если влиянием других факторов кроме x на результирующий признак у можно пренебречь, однако большинство моделей требует включения нескольких объясняющих переменных.

Модель множественной регрессии имеет вид:

(4.1)

где – объясняющие переменные (независимые переменные, факторы);

– объясняемая переменная (результирующий признак);

– неизвестные параметры модели (коэффициенты при объясняющих переменных);

– ошибки регрессии.

Чаще всего для построения уравнения множественной регрессии используют следующие виды функций:

1) линейная 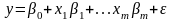(4.2)

2) степенная

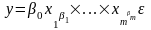(4.3)

где 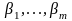- эластичность по факторам 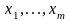соответственно;

3) экспонента 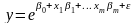(4.4)

4) гипербола 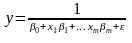(4.5)

Для построения модели множественной регрессии необходимо “правильно” отобрать объясняющие переменные, они должны:

1) существенно влиять на результирующий признак;

2) быть измеримы;

3) не должны быть сильно статистически зависимы попарно или в совокупности.

4.1. Нахождение оценок неизвестных параметров

Для нахождения неизвестных параметров множественной регрессии используется метод наименьших квадратов (МНК), минимизирующий отклонения результирующего признака у от теоретического (полученного из модели), то есть

(4.1.1)

При этом должны выполняться условия Гаусса – Маркова:

1.E( )=0, E( )=V( )= – не зависит от j, j=1…n.

Математическое ожидание ошибок равно нулю, дисперсия ошибок постоянна и не зависит от номера наблюдения.

2. E( )=0 при t  s, некоррелированность ошибок для разных наблюдений.

Ошибки независимы.

3. Ошибки , j=1…n, имеют совместное нормальное распределение ~ .

Рассмотрим случай линейной множественной регрессии:

.

Решением данной задачи являются оценки неизвестных параметров, которые находятся из решения системы уравнений:

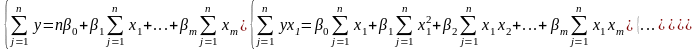(4.1.2)

Однако после нахождения оценок неизвестных параметров модели возникает вопрос о сравнимости влияния факторов на результирующий признак. Полученные оценки коэффициентов линейной регрессионной модели 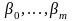нельзя использовать для сравнения влияния факторов , так как у них могут быть различные размерности (этаж, 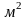, рубли, кг и т.д.) и разные выборочные дисперсии.

В данном случае рассматривается стандартизированное уравнение регрессии:

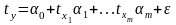(4.1.3)

где 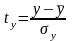, 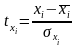- стандартизированы переменные для у и 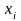соответственно;

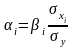- стандартизированные коэффициенты регрессии.

Стандартизированные коэффициенты регрессии являются безразмерными величинами, то есть, сравнивая их значения, можно оценить влияние различных факторов на результирующий признак.

К стандартизированному уравнению регрессии применим МНК. Если

- исходное уравнение регрессии;

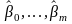- оценки коэффициентов, полученные путем МНК, тогда

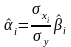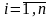, - МНК – оценка для стандартизированной переменной;

параметр определяется как .

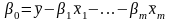Одним из наиболее важных показателей, используемых для оценки качества подгонки регрессионной модели к исходным статистическим данным является коэффициент детерминации (индекс множественной корреляции):

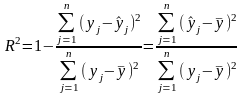(4.1.4)

Свойства коэффициента детерминации:

1) 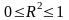: если 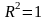=> 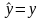, то есть полученные модельные значения полностью соответствуют исходным статистическим данным;

если 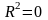, то полученная модель не объясняет поведение исследуемого ряда данных;

2) изменяется даже при простейшем преобразовании зависимой переменной, поэтому сравнивать по нему можно только регрессии с одинаковыми зависимыми переменными;

3) если в исследуемое уравнение регрессии добавить дополнительный фактор 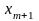, то новой модели будет больше или равен исходной модели, таким образом, если взять число регрессоров равным числу наблюдений (m=n), всегда можно добиться того, что , но это не будет означать наличие содержательной зависимости y от регрессоров.

Замечание: на практике для получения качественной модели число наблюдений (n) должно превосходить число регрессоров (m) в модели не менее чем в 8 раз.

Чтобы устранить эффект связанный с ростом при возрастании числа регрессоров является коррекция на число регрессоров: скорректированным коэффициентом детерминации называется

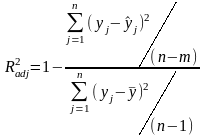(4.1.5)

где m – число регрессоров в модели,

n – число наблюдений.

Свойства скорректированного коэффициента детерминации:

1) ;

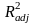
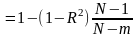2) , но он может быть отрицательным;

3) .

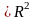Для оценки влияния фактора на у при исключении влияния остальных факторов (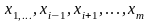 ) используют коэффициент частной корреляции:

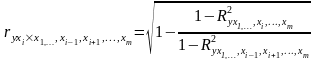(4.1.6)

Частные коэффициенты корреляции изменяются в пределах от -1 до 1.