19. Двойные интегралы

0. 19.1. Определение

Двойным интегралом от непрерывной функции , распространённым на ограниченную замкнутую плоскую область S, называется предел следующего вида

и обозначается

, (*)

где точка ( i = 1,2,...,n ) и d – наибольший диаметр площадок .

0. 19.2. Расстановка пределов интегрирования в двойном интеграле

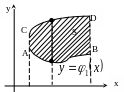
Различают два основных вида области интегрирования S :

а) Область S ограничена слева и справа прямыми и , а снизу и сверху соответственно непрерывными кривыми и (СD), каждая из которых пересекается с вертикалью только в одной точке. В этой области S переменная х изменяется от до , а переменная у при постоянном х меняется от до .

0

Для такой области интеграл (*) может быть вычислен путём сведения к повторному по формуле

,

где при вычислении внутреннего интеграла величину x полагают постоянной.

б) Область интегрирования S ограничена снизу и сверху прямыми и , а слева и справа- непрерывными кривыми (АВ), (СD), , каждая из которых пересекается с параллелью только в одной точке.

В этом случае имеем:

,

где во внутреннем интеграле y считается постоянной.

в) Если область интегрирования S не удовлетворяет ни одному из случаев а), б), то её стараются разбить на части, каждая из которых принадлежит к одному из этих случаев.

0. 19.3. Двойной интеграл в полярных координатах

Двойной интеграл в полярных координатах и , где

,

имеет вид:

.

Если область S определена неравенствами

,

то .

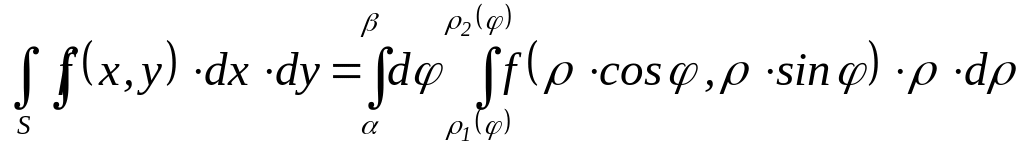19.4. Приложения двойных интегралов к геометрии

1. Площадь плоской фигуры

.

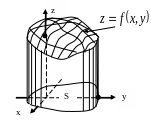
19.4.2. Объём цилиндроида Объём цилиндроида, ограниченного сверху непрерывной поверхностью , снизу плоскостью и с боков цилиндрической поверхностью , высекающей на плоскости xoy область S : 19.4.3.Площадь поверхности

Площадь P поверхности , имеющей своей проекцией на плоскость xoy область S , равна: .

19.5. Приложения двойных интегралов к механике

19.5.1. Масса пластинки

Масса пластинки S :

,

где - поверхностная плотность пластинки S. Если пластинка однородна, то

2. Статические моменты пластинки

Статические моменты пластинки S относительно координатных осей Ox и Oy выражаются интегралами

, .

2. Координаты центра тяжести пластинки

Координаты центра тяжести пластинки S определяются формулами:

,

где М – масса пластинки S , - её статические моменты относительно осей координат.

2. Моменты инерции пластинки

Моменты инерции пластинки S относительно осей Ox и Oy выражаются интегралами:

, .

Момент инерции пластинки S относительно начала координат определяется по формуле

.

19. Тройные интегралы