
- •Математические обозначения. Таблицы
- •Латинский алфавит
- •1.2. Греческий алфавит
- •1. 3. Математические обозначения
- •Некоторые исторические факты математических символов
- •Важнейшие постоянные
- •1.8. Некоторые степени чисел 2, 3, 5
- •1.9. Факториалы
- •Перевод градусной меры в радианную
- •Арифметика
- •Признаки делимости
- •2.2. Средние величины
- •Действительные числа
- •Действия над дробями
- •Пропорции
- •3.4. Абсолютная величина действительного числа (модуль)
- •Формулы сокращенного умножения
- •Квадратные уравнения
- •Разложение на множители
- •Аргумент, функция
- •Элементы поведения функции
- •Возрастающие и убывающие функции (монотонные функции)
- •Четные и нечётные функции
- •Периодические функции
- •Корни функции
- •Чтение графиков функций
- •3.11. Обратная функция
- •Проблема существования обратной функции
- •3.13. Основные элементарные функции
- •3.14. Степени и корни
- •3.16. Целая рациональная функция (или многочлен)
- •3.17. Квадратичная функция
- •3.18. Рациональная функция
- •3.19. Дробно-линейная функция
- •3.20. Показательная функция
- •3.21. Логарифмы. Логарифмическая функция
- •3.22. Гиперболические функции
- •Определения
- •Основные соотношения
- •3.22.3. Графики гиперболических функций
- •3.24. Соединения (размещения, перестановки, сочетания)
- •Бином ньютона
- •3.26. Комплексные числа
- •3.26.1. Комплексные числа в алгебраической форме
- •3.26.2. Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме
- •3.26.3. Показательная форма комплексного числа
- •3.27. Элементарные приёмы построения
- •3.27.1. Преобразования графиков
- •3.27.2. Сложение графиков
- •3.28. Графики некоторых функций, содержащие
- •3.29. Прогрессии
- •Арифметическая прогрессия
Элементы поведения функции
Возрастающие и убывающие функции (монотонные функции)
Функция
Если
для всех х
из
некоторого промежутка выполняется
неравенство
|
Функция
называется убывающее
на
отрезке
(на интервале, полуинтервале и т.д.),
если большему значению аргумента х
из этого промежутка
соответствует
меньшее
значение функции:
Если
для всех х
из
некоторого промежутка выполняется
неравенство
|
Функции возрастающие или убывающие на некотором промежутке называются монотонными. На
рисунке функция
не является монотонной на промежутке
|
|
Четные и нечётные функции
Функция
,
определённая на промежутке, симметричном
относительно х = 0, называется чётной,
если для любого значения х из этого
промежутка выполняется равенство
![]() ,
и нечётной,
если
,
и нечётной,
если
![]() .
.
Из этого определения следует, что график чётной функции симметричен относительно оси Оу, график нечётной функции симметричен относительно начала координат.
Это
график чётной
функции (симметричен относительно
оси Оу)
Проверим:
= . |
Г Проверим:
|
Периодические функции
Если график некоторой функции при смещении его на некоторый отрезок вдоль оси абсцисс (влево или вправо) совмещается сам с собой, то функция называется периодической. Длина этого отрезка Т называется периодом функции .
Это словесное
определение кратко записывается формулой
![]() .
.
Если Т – период функции, то 2Т, 3Т, -Т, -2Т, 3Т и т.д.- также периоды, т.е.
![]() ,
где n
– любое целое число.
,
где n
– любое целое число.
Корни функции
Значения х,
при которых значения функции
![]() ,
называются корнями
функции. На графиках - это абсциссы точек
пересечения графика функции с осью Ох.
,
называются корнями
функции. На графиках - это абсциссы точек
пересечения графика функции с осью Ох.
Чтение графиков функций
|
|
5.
6.
причём
в точке
в точках
|
|






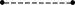

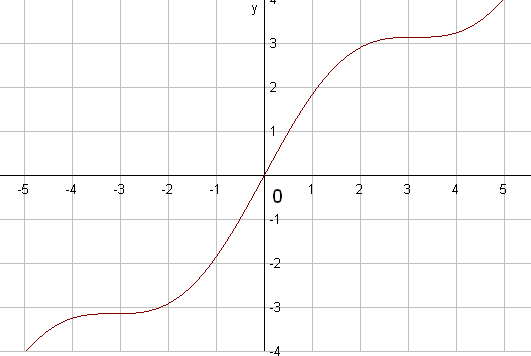
 рафик
нечётной
функции (симметричен относительно
начала координат)
рафик
нечётной
функции (симметричен относительно
начала координат)
