- •Математические обозначения. Таблицы
- •Латинский алфавит
- •1.2. Греческий алфавит
- •1. 3. Математические обозначения
- •Некоторые исторические факты математических символов
- •Важнейшие постоянные
- •1.8. Некоторые степени чисел 2, 3, 5
- •1.9. Факториалы
- •Перевод градусной меры в радианную
- •Арифметика
- •Признаки делимости
- •2.2. Средние величины
- •Действительные числа
- •Действия над дробями
- •Пропорции
- •3.4. Абсолютная величина действительного числа (модуль)
- •Формулы сокращенного умножения
- •Квадратные уравнения
- •Разложение на множители
- •Аргумент, функция
- •Элементы поведения функции
- •Возрастающие и убывающие функции (монотонные функции)
- •Четные и нечётные функции
- •Периодические функции
- •Корни функции
- •Чтение графиков функций
- •3.11. Обратная функция
- •Проблема существования обратной функции
- •3.13. Основные элементарные функции
- •3.14. Степени и корни
- •3.16. Целая рациональная функция (или многочлен)
- •3.17. Квадратичная функция
- •3.18. Рациональная функция
- •3.19. Дробно-линейная функция
- •3.20. Показательная функция
- •3.21. Логарифмы. Логарифмическая функция
- •3.22. Гиперболические функции
- •Определения
- •Основные соотношения
- •3.22.3. Графики гиперболических функций
- •3.24. Соединения (размещения, перестановки, сочетания)
- •Бином ньютона
- •3.26. Комплексные числа
- •3.26.1. Комплексные числа в алгебраической форме
- •3.26.2. Тригонометрическая форма комплексного числа
- •Действия над комплексными числами в тригонометрической форме
- •3.26.3. Показательная форма комплексного числа
- •3.27. Элементарные приёмы построения
- •3.27.1. Преобразования графиков
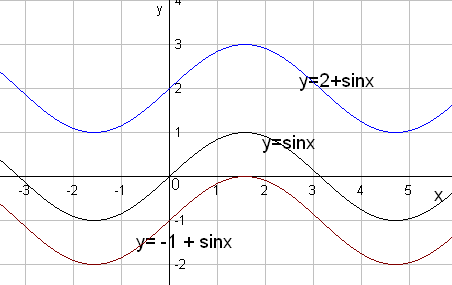
- •3.27.2. Сложение графиков
- •3.28. Графики некоторых функций, содержащие
- •3.29. Прогрессии
- •Арифметическая прогрессия
3.26. Комплексные числа
3.26.1. Комплексные числа в алгебраической форме
а) Определения.
Комплексным числом называется выражение вида
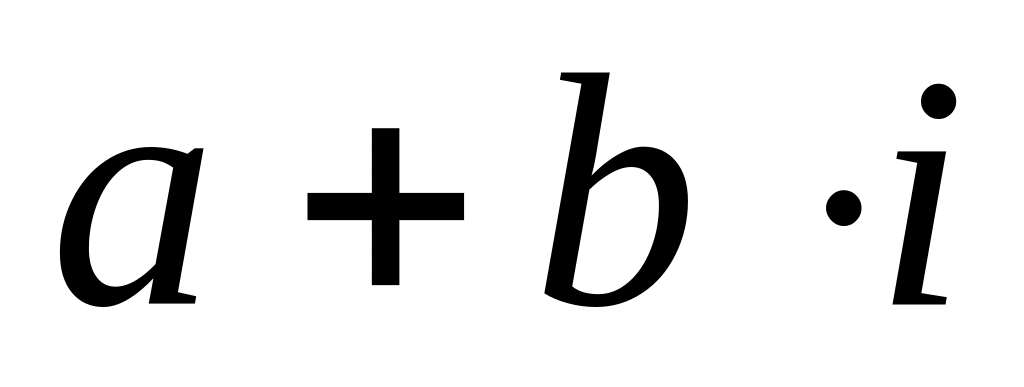 ,
в котором a
и b
– вещественные
числа (действительные), а i
- так называемая мнимая
единица –
число, квадрат которого считается
равным минус единице:
,
в котором a
и b
– вещественные
числа (действительные), а i
- так называемая мнимая
единица –
число, квадрат которого считается
равным минус единице:
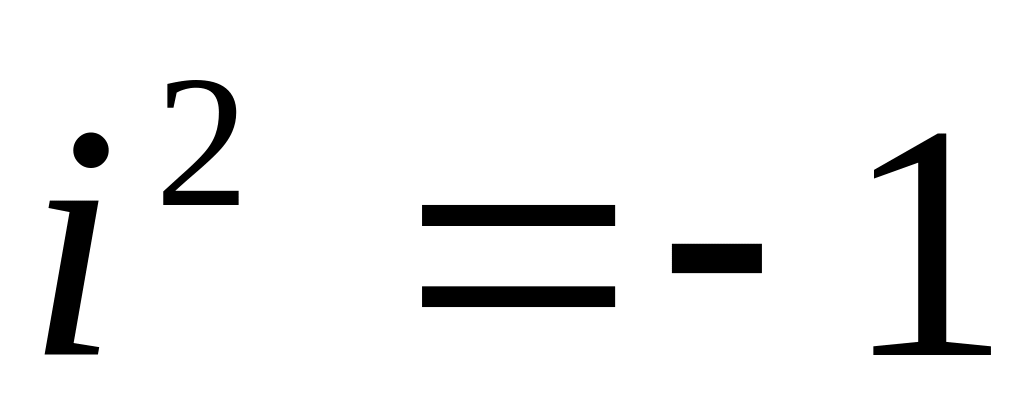 .
.
![]() -
вещественная
часть,
-
вещественная
часть,
![]() - мнимая
часть
комплексного
- мнимая
часть
комплексного
числа
Также
пишут
![]() .
.
Два комплексных числа
 и
и
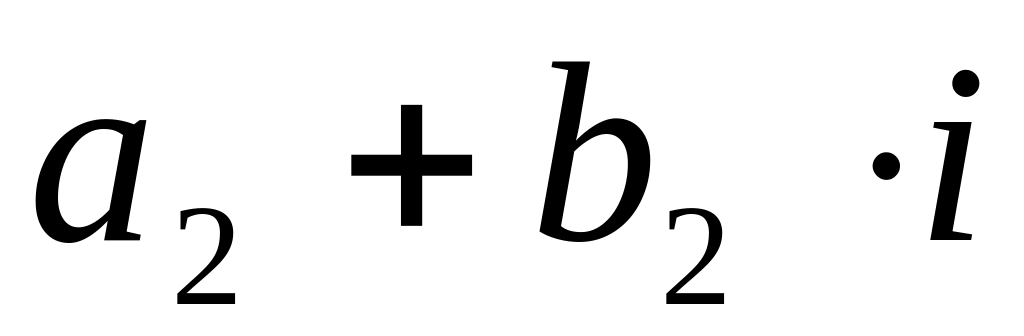 равны
тогда и только тогда, когда
равны
тогда и только тогда, когда
 и пишут :
и пишут :
= .
Комплексные числа вида
 условились считать равным вещественному
числу a.
Комплексное число вида
условились считать равным вещественному
числу a.
Комплексное число вида
 часто называют чисто
мнимым
числом.
часто называют чисто
мнимым
числом.Комплексные числа
 и
и
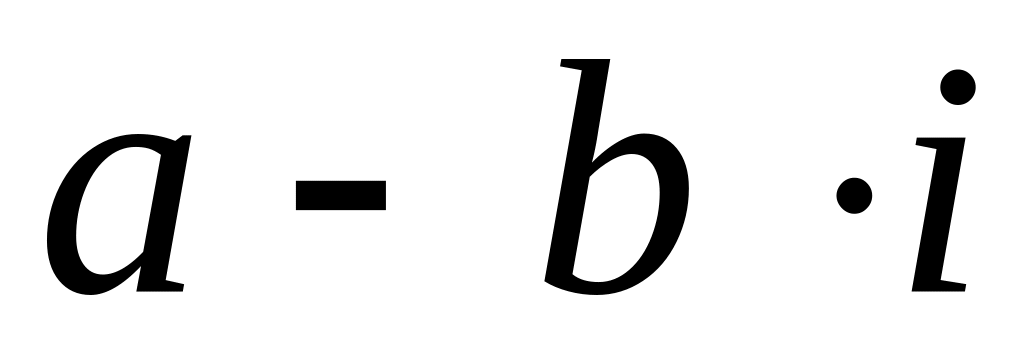 называются сопряженными.
называются сопряженными.
б). Действия над комплексными числами в алгебраической форме
Степени числа
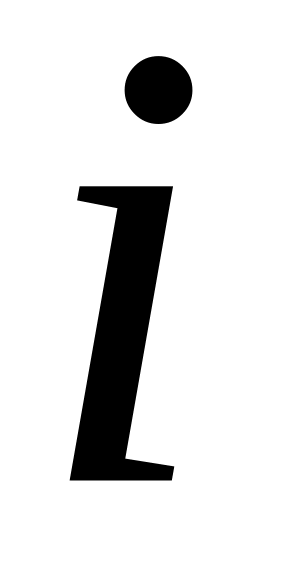 .
.
Сложение, вычитание, умножение и возведение в целую положительную степень комплексных чисел можно выполнять по правилам этих действий над обычными алгебраическими выражениями, но с заменой степеней числа .
Деление комплексных чисел:
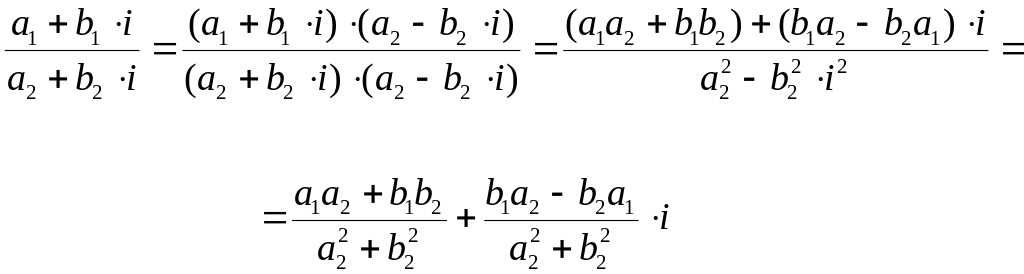
3.26.2. Тригонометрическая форма комплексного числа
 1. Комплексное
число
1. Комплексное
число
![]() определяется парой вещественных чисел
определяется парой вещественных чисел
![]() и
и
![]() .
Это позволяет изображать комплексные
числа как точки
.
Это позволяет изображать комплексные
числа как точки
![]() плоскости в декартовой (прямоугольной)
системе координат или радиусом-вектором
этой точки
плоскости в декартовой (прямоугольной)
системе координат или радиусом-вектором
этой точки
![]() .
.
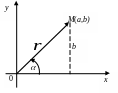
2. Модулем
комплексного
числа называется
длина вектора
![]() ,
угол
,
угол
![]() называется аргументом
комплексного
числа.
называется аргументом
комплексного
числа.
3. Из прямоугольного треугольника OAM имеем:
![]() ,
,
тогда
![]() )
-
)
-
тригонометрическая форма комплексного числа.
Действия над комплексными числами в тригонометрической форме
Умножение. Пусть даны два комплексных числа:
![]()
тогда
![]() .
.
Деление:
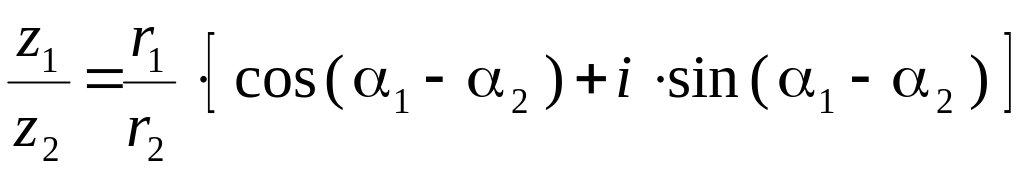 .
.
Возведение в степень:
 .
.
Извлечение корня:
![]() =
=![]()
где
![]()
,
Формулы возведения в степень и извлечения корня называются формулами Муавра.
3.26.3. Показательная форма комплексного числа
![]() .
.
ДЛЯ ЗАМЕТОК.
3.27. Элементарные приёмы построения
ГРАФИКОВ ФУНКЦИЙ
3.27.1. Преобразования графиков
Исходя из графика функции , можно построить графики
функций:
 - первоначальный
график отображается симметрично оси
Ох (“зеркальное отображение” ).
- первоначальный
график отображается симметрично оси
Ох (“зеркальное отображение” ).
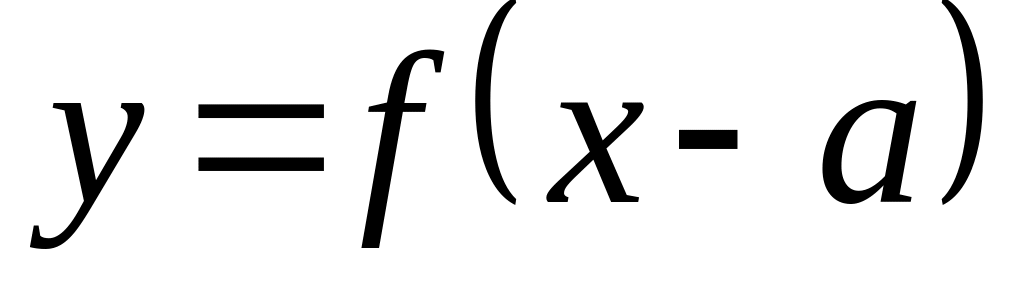 - первоначальный
график
сдвигается
вдоль оси Ох
на величину
а
вправо,
если
- первоначальный
график
сдвигается
вдоль оси Ох
на величину
а
вправо,
если
 и влево, если
и влево, если
 .
.
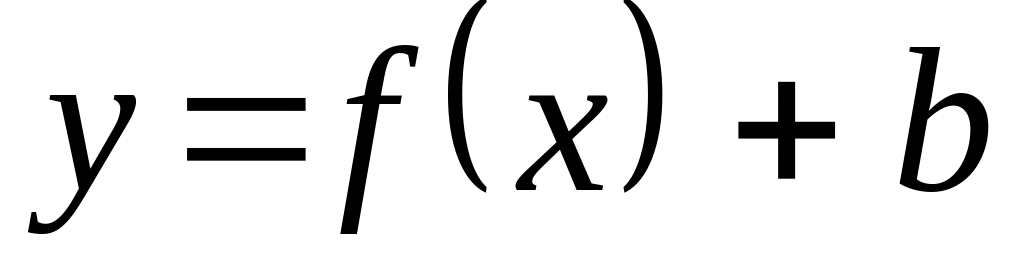 - исходный график
перемещается
вдоль оси
Оу на
величину
- исходный график
перемещается
вдоль оси
Оу на
величину
 :
вверх,
если
:
вверх,
если
 ,
и вниз,
если
,
и вниз,
если
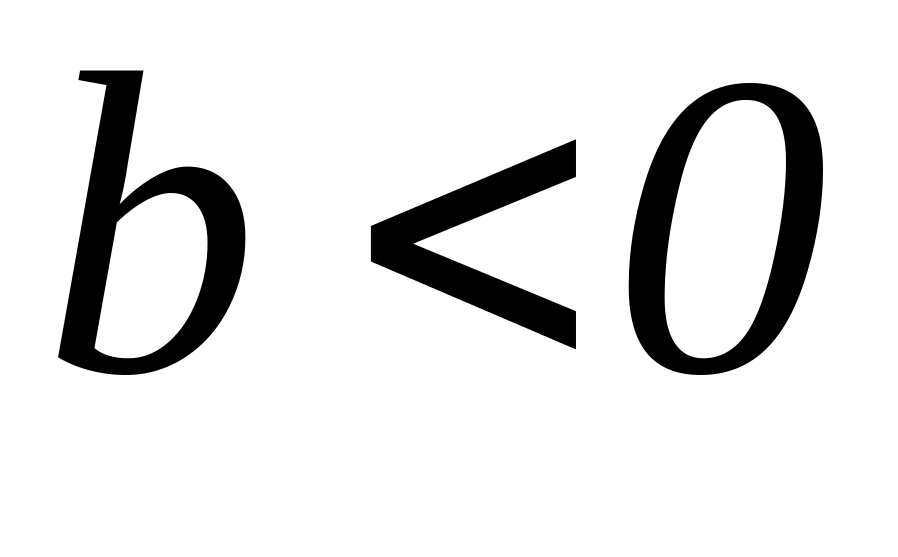 .
.
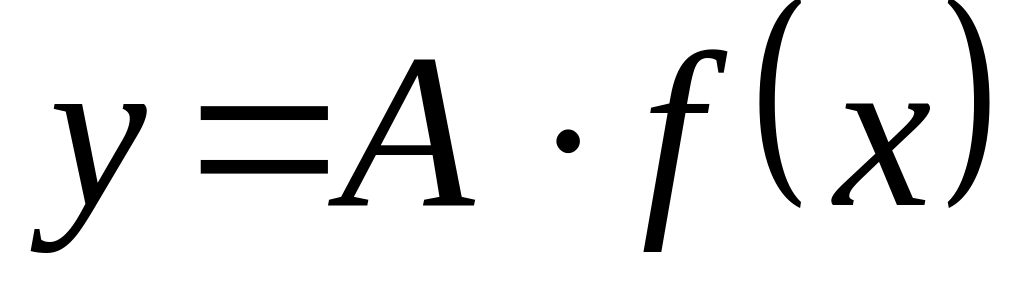 - исходный
график
растягивается
вдоль оси
Оу в А раз
(если А>1) и сжимается
в
- исходный
график
растягивается
вдоль оси
Оу в А раз
(если А>1) и сжимается
в
 раз, если
раз, если
 .
.
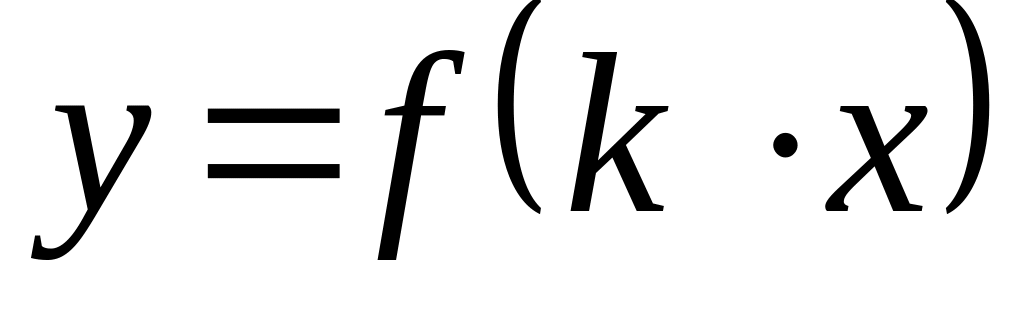 - тот
же график, но растянутый
вдоль оси
Ох от начала
координат в
- тот
же график, но растянутый
вдоль оси
Ох от начала
координат в
 раз.
раз.
Таким образом, используя график функции , можно построить график функции
6.
![]() .
.
Примеры.
1).
,
![]() 2).
2).
|
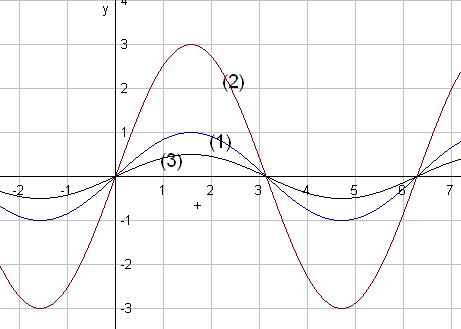
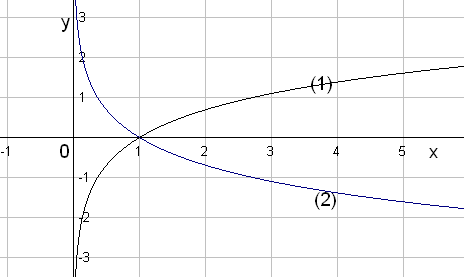
(1): (2):
(3) :
|
3). 4).
Примеры.
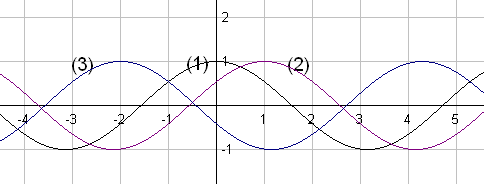
(1)
(2) :
(3) :
|
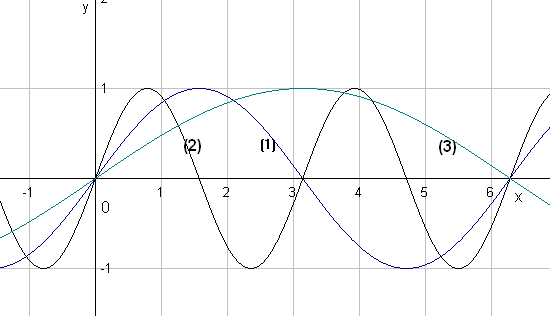
Примеры. (1) : ; (2) :
(3):
|
5).
|
Примеры. (1):
(2):
(3):
|
6).
![]()
|
Пример.
Приведём
к виду:
Строим цепочку графиков в следующей последовательности:
6.
|

 Примеры.
Примеры.