Задания для самостоятельного решения
1. Установить, какие кривые определяются нижеследующими уравнениями. Построить чертежи.
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
и)
.
2. Привести к каноническому виду уравнения следующих кривых:
а)
;
б)
;
в)
.
8. Инварианты уравнения второй степени
При переходе от одной системы прямоугольных координат к другой мы заменяем уравнение
(1)
линии второго порядка другим уравнение
, (2)
которое получается из (1) с помощью формул преобразования координат. При этом значения A’, B’, C’, D’, E’, F’ (все или некоторые) отличаются от значений одноименных величин A, B, C, D, E, F .
Однако три нижеприведенных выражения, составленных из величин A’, B’, C’, D’, E’, F’, всегда остаются равными одноименным выражениям, составленным из величин A, B, C, D, E, F . Эти три выражения называются инвариантами уравнения второй степени.
а) A + C.
б) Второй инвариант
(малый дискриминант).
в) Третий дискриминант
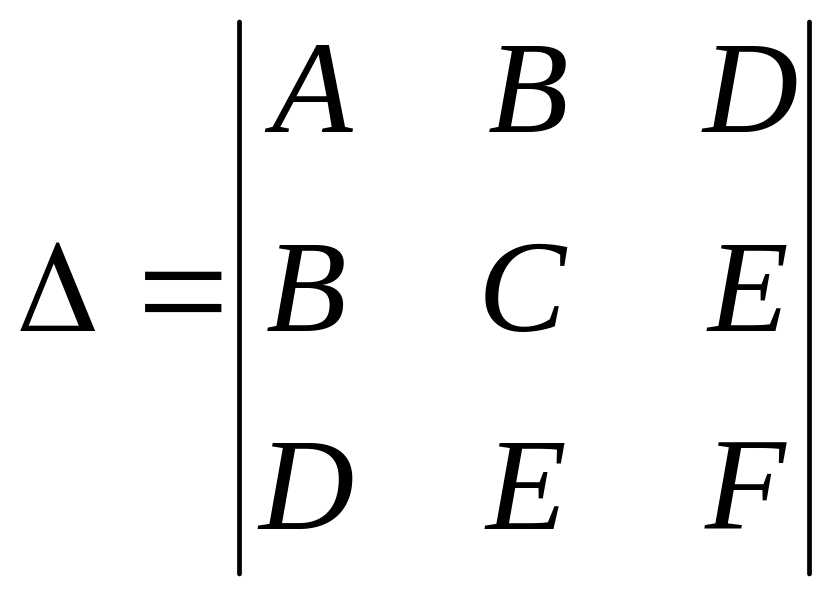(большой дискриминант).
Пример. Уравнение
преобразуем к виду
соответственно повороту осей на угол
.
а) Выражение A + C в старой системе равнялось 2 + 5 = 7, в новой системе одноименное выражение A’ + C’ равняется 1 + 6 = 7, так что
A + C = A’ + C’.
б) Малый дискриминант в старой системе координат был равен
,
а в новой системе имеем:
,
так что 
.
в) Большой дискриминант в старой системе был равен
,
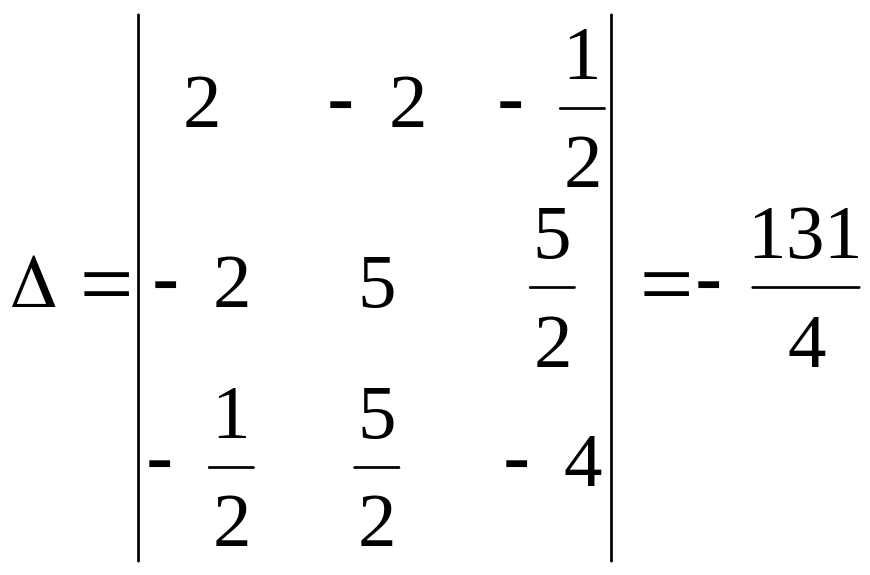в новой системе
,
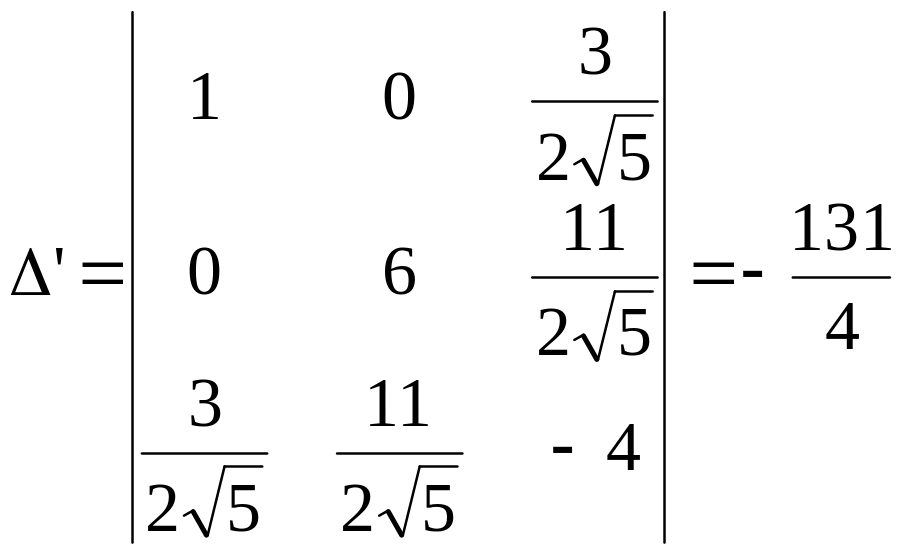так что
.
Основная литература
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры : учебник / Д.В. Беклемишев. – М. : Высш. шк., 1998. – 319с.
Данко П.Е Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я.Кожевникова. – М. : Высш. шк., 1999. – Ч.1. – 304 с.
ШипачевВ.С. Основы высшей математики : учеб. пособие / В.С. Шипачев. – М. : Высш. шк., 1998. – 479с.
Дополнительная литература
Минорский В.П. Сборник задач по высшей математике / В.П. Минорский. – М. : Наука, 1969. – 352 с.
Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии / О.Н. Цубербиллер. – М. : Наука. 1966. – 336 с.
Содержание
1. Окружность 3
2. Эллипс 7
3. Гипербола 9
4. Парабола 13
5. Диаметры и касательные к кривым 2-го порядка 16
6. Линии второго порядка 18
7. Пятичленное уравнение кривой второго порядка 20
8. Инварианты уравнения второй степени 22
Основная литература 23
Составитель Петрова Елена Владимировна
Редактор Тихомирова О.А.