
- •3.3.2. Методы прогнозирования
- •Экспертные методы
- •Методика проведения индивидуальной разовой экспертной опенки
- •Статистический анализ временных рядов
- •Прогнозирование методом простого среднего
- •Прогнозирование метолом «скользящего» среднего
- •Прогнозирование метолом экспоненциального сглаживании
- •Факторный анализ статистик
- •3.3.3. Проверка и корректировка прогнозов
- •Диаграмма со скользящим шагом
Факторный анализ статистик
Если значения прогнозируемого параметра зависят не от времени, а от каких-либо других факторов, то используется факторный статистический анализ. Обычно для этого с помощью ПЭВМ по известной статистике подбирается аппроксимирующая функция одной или многих переменных, которая и служит моделью для выработки прогноза. Рассмотрим эту процедуру на примере.
Пример.
Предприниматель реализует мороженное у станции метро "Политехническая". Он должен сделать заказ на будущую педелю с разбивкой по дням. Каждое утро заказанное количество товара завозится на его точки реализации. При неправильном заказе (прогнозе) в конце дня мороженного может не хватить тогда имеет место упущенная выгода, либо часть его останется нереализованной и тогда возникнут проблемы с его сохранением до завтрашнего утра. Требуется выявить факторы, определяющие продажи, собрать статистику продаж и значений этих факторов, далее разработать прогноз продаж мороженного на будущую неделю. Предполагается, что дело происходит в разгаре лета.
Решение.
Среди факторов, влияющих на продажи мороженного в разгар лета, отобраны два наиболее существенных: температура воздуха и день недели. Отметим, что второй фактор имеет логический характер, что создает дополнительные трудности решения. Собранная за три недели статистика представлена в таблице 3.1. Будем считать, что к моменту прогнозирования объема продаж известен прогноз погоды (температуры) на будущую неделю.
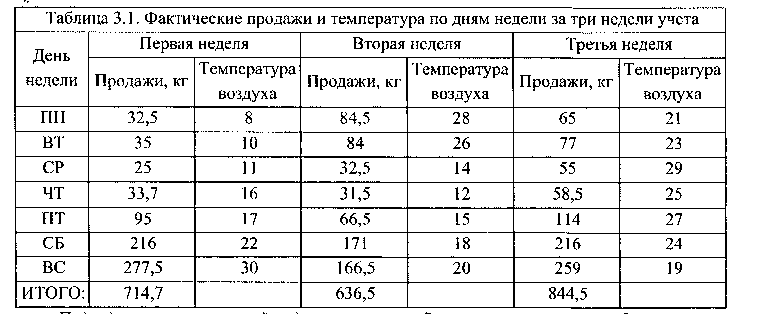
Подходов к решению этой задачи несколько. Рассмотри» сначала наиболее распространенный классический метод.
Для устранения влияния на зависимость продаж от температуры логической переменной — дня недели рассчитаем коэффициенты приведения для каждого дня недели к среднедневной продаже (табл.. 3.2). Затем с помощью этих коэффициентов пересчитаем исходные данные о продажах (получим приверженные фактические продажи. показанные в табл..3.3
и на рис. 3.2). Аппроксимация этой зависимости прямой, описываемой уравнением 0=4,1 t0+23,76. дает очень хорошие результаты (коэф. корреляции 0,9). В табл.. 3.3 даны также результаты расчетов продаж на основе полученной трендовой линейной зависимости. С использованием этой же модели можно спрогнозировать приведенные продажи на будущую неделю, а затем с помощью коэффициентов приведения перечитать их в индивидуальные прогнозы на каждый день недели (табл. 3.4).


Значения коэффициентов а и в при линейной аппроксимации могут быть рассчитаны как на ПЭВМ, так и вручную по формулам

Попытка связать объемы продаж только с температурой, игнорируя влияние на них дня недели, несостоятельна. Это наглядно видно из графика (рис. 3.1) и значения коэффициента корреляции.
Другой, менее точный подход к решению состоит в том, чтобы в единый статистический массив свести данные с понедельника по четверг без разделения их на дни педели. То же проделать с данными пятницы, субботы и воскресенья. Для каждого из массивов подобрать аппроксимирующую кривую зависимости объемов продаж от температуры и на ее основе делать прогноз.
При наличии большей, чем сейчас, статистики эту процедуру можно осуществлять отдельно для каждого дня недели, что упростит и сделает более точным решение этой задачи. При этом плохо лишь то, что с ростом объема статистик на прогноз все большее влияние будет оказывать фактор сезонности, который мы до сих пор игнорировали.

