
- •Понятие базиса.
- •Проекция вектора на ось.
- •Свойства проекции вектора на ось.
- •Направляющие косинусы.
- •Скалярное произведение векторов.
- •Геометрические свойства скалярного произведения.
- •Алгебраические свойства скалярного произведения.
- •Выражение скалярного произведения через координаты векторов.
- •Векторное произведение векторов. Правые и левые тройки векторов и системы координат.
- •Геометрические свойства векторного произведения.
- •Геометрическое построение векторного произведения.
- •Выражение векторного произведения через координаты векторов.
- •Смешанное произведение векторов.
- •Геометрический смысл смешанного произведения.
- •Свойства смешанного произведения.
- •Выражение смешанного произведения через координаты векторов.
- •Приложение смешанного произведения.
Понятие базиса.
Определение.
Три линейно независимых вектора
 ,
, и
и образуют в пространствебазис,
если любой вектор
образуют в пространствебазис,
если любой вектор
 может быть представлен в виде некоторой
линейной комбинации векторов
может быть представлен в виде некоторой
линейной комбинации векторов ,
, и
и ,
т.е. если для вектора
,
т.е. если для вектора найдутся такие вещественные числа,
,
,
что справедливо равенство:
найдутся такие вещественные числа,
,
,
что справедливо равенство:
 =
= +
+ +
+ (1)
(1)
Определение.
Два лежащих
в плоскости
линейно независимых вектора
 и
и образуют на этой плоскости базис, если
любой лежащий в плоскости
вектор
образуют на этой плоскости базис, если
любой лежащий в плоскости
вектор
 может быть представлен в виде некоторой
линейной комбинации векторов
может быть представлен в виде некоторой
линейной комбинации векторов и
и ,
т.е. если для любого лежащего в плоскости
вектора
,
т.е. если для любого лежащего в плоскости
вектора
 найдутся такие вещественные числа
и ,
что справедливо равенство :
найдутся такие вещественные числа
и ,
что справедливо равенство :  =
=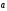 +
+ (2)
(2)
Утверждения.
1)
любая тройка некомпланарных
векторов
 ,
, и
и образует базис впространстве;
образует базис впространстве;
2)
любая пара лежащих в данной плоскости
неколлинеарных векторов
 и
и образует базис на этой плоскости.
образует базис на этой плоскости.
В дальнейшем для определенности будем рассматривать базис в пространстве.
Пусть
 ,
, и
и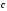 - произвольный базис в пространстве
(т.е. произвольная тройка некомпланарных
векторов). Тогда равенство
- произвольный базис в пространстве
(т.е. произвольная тройка некомпланарных
векторов). Тогда равенство =
= +
+ +
+ называется разложением
вектора
называется разложением
вектора
 по базису
по базису ,
, ,
,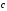 ,
а числа ,
,
- координаты
вектора
,
а числа ,
,
- координаты
вектора
 относительно базиса
относительно базиса
 ,
, ,
, .
.
Покажем
единственность разложения вектора
 по базису
по базису
 ,
, ,
,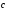 .Допустим
противное, что наряду с разложением
(1), справедливо еще и другое разложение
по этому же базису:
.Допустим
противное, что наряду с разложением
(1), справедливо еще и другое разложение
по этому же базису:
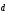 =
= +
+ +
+ (3)
(3)
Вычитая из (1) из (3) получаем:
(-) +(-)
+(-) +(-)
+(-) =0
=0
В
силу линейной независимости базисных
векторов
 ,
, ,
, последнее соотношение приводит к
равенству:-=0,
-=0,
-=0
или =,
=,
=.
последнее соотношение приводит к
равенству:-=0,
-=0,
-=0
или =,
=,
=.
Теорема.
При сложении двух векторов
 и
и их координаты (относительно любого
базиса
их координаты (относительно любого
базиса ,
,
 ,
, )складываются.
При умножении вектора
)складываются.
При умножении вектора
 на любое число
все его координаты умножаются на это
число.
на любое число
все его координаты умножаются на это
число.
Доказательство.
Пусть
 =1
=1 +1
+1 +1
+1 ,
,
 =2
=2 +2
+2 +2
+2 .
Тогда в силу свойств линейных операций:
.
Тогда в силу свойств линейных операций:
 +
+ =(1+2)
=(1+2) +(1+2)
+(1+2) +(1+2)
+(1+2) ,
,
 =(1)
=(1) +(1)
+(1) +(1)
+(1)
В силу единственности разложения по базису ч.т.д.
Проекция вектора на ось.
(Ортогональная) проекция точки на ось – основание перпендикуляра, опущенного из точки на данную ось. (рисунок)
l
 на осьu
называется величина (длина) вектора
на осьu
называется величина (длина) вектора
 ,
проведенного из проекции начала в
проекцию конца вектора
,
проведенного из проекции начала в
проекцию конца вектора ,
взятая со знаком “+”, если направление
вектора
,
взятая со знаком “+”, если направление
вектора совпадает с направлением осиu
и со знаком “-” в противном случае.
совпадает с направлением осиu
и со знаком “-” в противном случае.
Свойства проекции вектора на ось.
Проекция суммы (разности) двух векторов равна сумме (разности) проекций векторов на ось
прu( )=
)=
Постоянный множитель можно выносить за знак проекции:

Угол наклона
вектора
 =
= к оси u
определяется как угол
между двумя выходящими из произвольной
точки М лучами, один из которых имеет
направление, совпадающее с направлением
вектора
к оси u
определяется как угол
между двумя выходящими из произвольной
точки М лучами, один из которых имеет
направление, совпадающее с направлением
вектора
 =
= ,
а другой – направление, совпадающее с
направлением оси u.
(Рисунок)
,
а другой – направление, совпадающее с
направлением оси u.
(Рисунок)
На величину угла
наклона вектора
 к осиu
не влияют выбор точки М выхода указанных
лучей и замена оси u
любой другой осью v,
имеющей то же направление, что и ось u.
к осиu
не влияют выбор точки М выхода указанных
лучей и замена оси u
любой другой осью v,
имеющей то же направление, что и ось u.
Теорема.
Проекция
вектора
 на осьu
равна произведению длины
на осьu
равна произведению длины
 на косинус угла φ наклона вектора
на косинус угла φ наклона вектора к осиu:
к осиu:
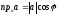 .
.
Доказательство.
Обозначим через v
ось, проходящую через начало А вектора
 и имеющую то же направлении, что осьu,
и пусть С – проекция В на ось v.
Тогда ВАС=,
где
- угол наклона вектора
и имеющую то же направлении, что осьu,
и пусть С – проекция В на ось v.
Тогда ВАС=,
где
- угол наклона вектора
 =
= к любой из осей u
или v,
причем точка С лежит в указанной
проецирующей плоскости (т.е.
в плоскости, перпендикулярной оси u
и проходящей через точку В). (Рисунок)
к любой из осей u
или v,
причем точка С лежит в указанной
проецирующей плоскости (т.е.
в плоскости, перпендикулярной оси u
и проходящей через точку В). (Рисунок)
А1В1=АС
(А1В1–величина
вектора
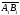 оси u,
а АС–величина
вектора
оси u,
а АС–величина
вектора
 оси v),
т.к. оси u
и v
параллельны и одинаково направлены и
отрезки этих осей заключенные между
параллельными плоскостями
и ,
равны. Т.к. по определению
оси v),
т.к. оси u
и v
параллельны и одинаково направлены и
отрезки этих осей заключенные между
параллельными плоскостями
и ,
равны. Т.к. по определению
 ,
то получаем равенство:
,
то получаем равенство:  =АС (1)
=АС (1)
Но величина АС
представляет собой проекцию вектора
 на ось v
и
на ось v
и
АС= =
= (2)
(2)
Сопоставляя 91) и
(20, получим
 ч.т.д.
ч.т.д.
Аффинные координаты (от лат. affinis – соседний, смежный).
Аффинные
координаты в пространстве определяются
заданием базиса
 ,
,
 ,
,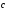 и некоторой
точкой О, называемой началом координат.
и некоторой
точкой О, называемой началом координат.
Аффинными
координатами любой точки М называются
координаты вектора
 (относительно базиса
(относительно базиса ,
,
 ,
, ).
Т.к. каждый вектор
).
Т.к. каждый вектор
 может быть единственным образом разложен
по базису
может быть единственным образом разложен
по базису ,
,
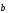 ,
, ,
то каждой точке пространства М однозначно
соответствует тройка аффинных координат
,
,
.
,
то каждой точке пространства М однозначно
соответствует тройка аффинных координат
,
,
.
Декартова прямоугольная система координат является частным случаем аффинной системы координат, отвечающей тройке взаимно ортогональных единичных базисных векторов.
 Ох
– ось абсцисс, Оу – ось ординат, Оz –
ось аппликат.
Ох
– ось абсцисс, Оу – ось ординат, Оz –
ось аппликат.
Базисные
векторы принято обозначать
 - три взаимно ортогональных единичных
вектора.
- три взаимно ортогональных единичных
вектора.
Любой
вектор
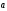 (
( )
можно единственным образом разложить
по декартовому базису с коэффициентами
ах,
ay,
az
(X,Y,Z):
)
можно единственным образом разложить
по декартовому базису с коэффициентами
ах,
ay,
az
(X,Y,Z):
 .
.
Коэффициенты
ах,
ay,
az называются
декартовыми
прямоугольными
координатами
вектора
 в базисе
в базисе .
.
Если
М – любая точка пространства, то декартовы
координаты этой точки совпадают с
декартовыми координатами вектора
 .
.
Координатами
вектора
 называют координаты его конечной точки.
(на рис. коорд. вектора
называют координаты его конечной точки.
(на рис. коорд. вектора =
= на плоскости
на плоскости ={х,у},
в пространстве -
={х,у},
в пространстве - ={x,y,z}).
={x,y,z}).
Теорема.
Декартовы прямоугольные координаты
X,Y,Z
вектора
 равны проекциям этого вектора на осиOx,
Oy,
Oz.
равны проекциям этого вектора на осиOx,
Oy,
Oz.
(Доказательство на стр. 61)
