Случайные векторы Системы случайных величин

(Х₁,Х₂,…,Х_n)

Совокупность случайных величин Х₁,Х₂,…,Х_nназываетсяслучайным вектором, многомерной случайной величиной, системой случайных величин.

Случайные вектора могут быть дискретными и непрерывными:

Например:

Х₁– рост человека Х₂– вес человека

Вектор (Х₁,Х₂) – непрерывный двумерный случайный вектор.

Случайный вектор полностью описывается его функцией распределения.

Функция распределения случайного вектора F(x₁,x₂,…,x_n) (-∞<x₁,x₂,…,x_n<∞) равна вероятности того, что в результате опыта случайные величиныx₁,x₂,…,x_nпримут такие значения, чтоX₁<x₁,X₂<x₂,…,X_n<x_n.

F(x₁,x₂,…,x_n)=P(X_k<x_k,k=1,2,..,n) (1)

Ее геометрическое значениеравно вероятность того, что случайная точка попадет в бесконечныйn-мерный параллелепипед с одной единственной конечной точкой (вершиной) (x₁,x₂,…,x_n) (имеющая максимальные координаты).

В двумерном случае попадание в заштрихованную область.

Функция распределения (1) обладает следующими свойствами:

1. 0≤f(x₁,x₂,…,x_n)≤1, (-∞<x₁,x₂,…,x_n<∞)

2. F(-∞,-∞,…,-∞)=0

3. F(∞,∞,…,∞)=1

4. F(x₁`,x<sub>2</sub>`,…,x_n`)≤F(x₁``,x<sub>2</sub>``,…,x_n``)

x₁`≤x<sub>1</sub>``,x<sub>2</sub>`≤x₂``,…,x<sub>n</sub>``≤x_n``

(2)

Зная плотность вероятности функцию распределения можно найти по формуле:

(3)

(4)

(5)

(6)

n– мерная случайная точка попадет вn– мерную область В.

(7)

Если вектор (Х₁,Х₂,…,Х_n) является дискретным, то в этом случе плотность вероятности не имеет смысла, тогда в роли вероятности выступают следующие:

(8)

Суммирование происходит по индексам, которые соответствуют всем возможным значениям:

(9)

(10)

Формулы (1) – (10) являются аналогами формул для одной случайной величины:

F(x)=P(X<x) (1`)

(2`)

(3`)

(4`)

(5`)

(6`)

(7`)

(8`)

(9`)

(10`)

Если в функции F(x₁,x₂,…,x_n) задать некоторые переменные =∞, то получим функцию распределения, соответствующую вектору для остальных переменных.

F(x₁,x₂,…,x_k,∞,…,∞)=P(X₁<x₁,…,X_k<x_k,X_k+1< ∞,…,X_n<∞)=F_1,2,..,k(x₁,x₂,…,x_k) (11)

(12)

Условные законы распределения

Если какие-либо компоненты вектора (Х₁,Х₂,…,Х_n) в результате опыта приняли какие- -либо значения, то закон распределения случайного вектора, состоящего из остальных компонент называют условным законом распределения этого вектора.

(Х₁,Х₂,…,Х_n)

(13)

(14)

(15)

Можно заметить что (14) получилась путем интегрирования (13) по переменным , (13) же есть аналог:

А эта формула следует непосредственно из теоремы умножения:

Р(А₁А₂А₃…А_n)= Р(А₁)P(А₂/ А₁)…P(А_n/ А₁А₂…А_n-1)

f(x₁x₂x₃…x_n)=f(x₁)f(x₂/x₁)…f(x_n/x₁x₂…x_n-1) (16)

(17)

(18)

Случайные величины называют независимыми, если:

(19)

Тогда для независимых величин получается:

(20)

Дискретный вектор:

(13`)

(14`)

(15`)

(16`)

(17`)

(18`)

(1)

(Х₁,Х₂,…,Х_n) – непрерывный случайный вектор

Аналогом (1) тогда для этого вектора является:

(2)

1)

(3)

2)

3)

4)

5)

(корреляционный моментслучайных величин)

Корреляционный моментхарактеризует силу связи между случайными величинами

Свойства:

1. 

2. 

3. 

Доказательствотретьего свойства:

Случайные величины, для которых К=0, называют некоррелированными.

Независимые случайные величины являются некоррелированными, но не наоборот.

Пусть Х₁– случайная непрерывная величина, плотность вероятности которой симметрична относительно оси ординат, т.е. математическое ожидание =0:

если они некоррелированные, это не значит что они независимы.

Безразмерной характеристикой степени связи между случайными величинами называют коэффициент корреляции:

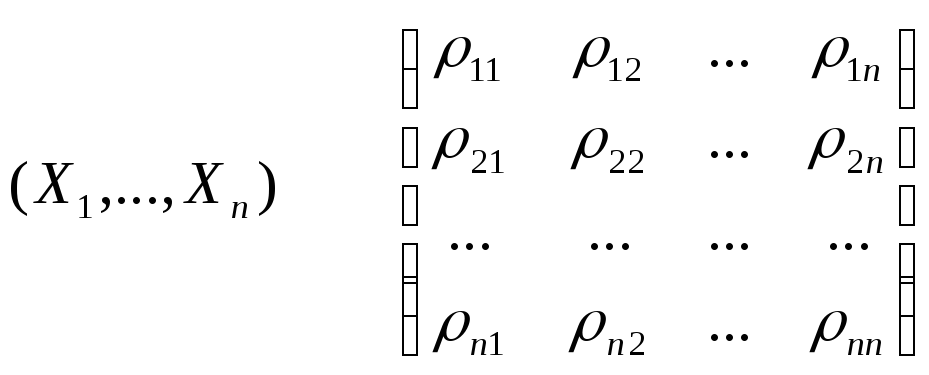
Свойства:

1. 

2. 

3. 

Дисперсия суммы попарно некоррелированных случайных величин равна сумме дисперсий:

Условное математическое ожидание:

Для непрерывного вектора:

(1)

(2)

(3)

Для дискретного вектора: