Предмет теории вероятностей

Тория вероятностей– раздел математики в котором изучают закономерности случайных явлений, которые наблюдаются при повторении опытов.

Предметом теориивероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.

Достоверное событие– событие (Ω), которое наступит в результате каждого опыта.

Невозможное событие– событие (θ), которое не наступит в каждом опыте.

Случайное событие– событие, наступление которого заранее предугадать не возможно.

Примеры:

• Бросание обычной монеты есть опыт.

• Выпадение герба (цифры) есть случайное событие.

• Выпадение герба или цифры есть достоверное событие.

• Выпадение ребра есть невозможное событие.

Алгебра событий

Событие А и В называются равносильнымиесли наступление одного из них происходит тогда и только тогда, когда другое наступило в том же самом опыте.А=В

Суммой N событийназывается событие, состоящее в наступлении хотя бы одного из этих событий в результате опыта. А₁+А₂+А₃+ … +А_nА₁А₂А₃…А_n

Произведением N событийназывается событие, состоящее в совместном наступлении всех этих событий в результате опыта. А₁А₂А₃…А_nА₁А₂А₃…А_n

А+В=В+А

АВ=ВА

(А+В)+С=А+(В+С) (АВ)С=А(ВС)

(А+В)C=AC+BC

Aθ=θ

АΩ=А

А+А=А

АА=А

А–В=А

Диаграммы Венна

События А₁,А₂,А₃… А_nназываютсянесовместными, если наступление одного из них исключает наступление других в одном и том же опыте.

А_iА_j=θi,j=1,2,…,n

Если события А₁,А₂,А₃… А_nнесовместны, то их сумма есть событие, состоящее в наступлении одного и только одного события.

А₁+А₂+А₃+ … +А_n=А₂

i=1,2,3.

Пусть А – некоторое событие, тогда событие, состоящее в том, что событие а не происходит в результате опыта называется противоположным событием ().

А+=Ω

А₁А₂А₃…А_n=θ

Если А₁,А₂,А₃, … ,А_n– несовместны, то их произведение есть невозможное событие.

А=θ

Частота событий и ее свойства

Относительной частотой события А () называется отношение числаmопытов в которых событие А наступило к общему числуn– фактически проведенных опытов.

(1)

Условной частотой события В по отношению в событию А () называется отношение числаkопытов, в которых наступило событие А и В к опытамmв которых наступило событие А.

(2)

Аксиоматическое определение вероятности

В теории вероятности каждого события ставится в соответствие определенное число Р(А), которое называется вероятностью события А, причем эта вероятность удовлетворяет следующим аксиомам:

1. 

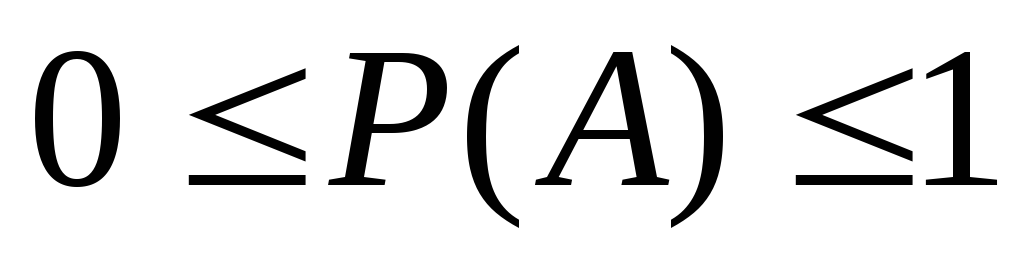
2. Р(Ω)=1

3. Р(θ)=0

4. А и В – несовместные события: Р(А+В)=Р(А)+Р(В)

5. Р(АВ)=Р(А)Р(В/А) Р(В/А) – условная вероятность

Вероятность события В определяется при условии, что событие А уже наступило.

Примечание:

На практике часть вероятностей не известна, в этом случае используют соответствующую частоту, это делается на основании больших чисел.

Если вероятность события очень мала на практике, то такое событие считают невозможным.

Если вероятность ≈1, то такое событие считают достоверным.

Независимость событий

Событие А и В называют независимыми, если вероятность каждого из них не зависит от того наступило или нет другое событие.

(3)

(4)

Пусть для некоторых А и В выполняется (4) тогда из аксиомы умножения следует (3) и следовательно А и В независимы.

События А₁,А₂,А₃, … ,А_n независимы в совокупности, если каждое из этих событий и любая комбинация остальных является независимыми событиями.

- независимы

Теорема умножения вероятностей

Р(А₁А₂А₃…А_n)=Р(А₁)P(А₂А₃…А_n/ А₁)=

= Р(А₁)P(А₂/ А₁)P(А₃…А_n/ А₁А₂)= Р(А₁)P(А₂/ А₁)…P(А_n/ А₁А₂…А_n-1)

Вероятность произведения событий равно произведению вероятностей этих событий, определяемых при условии, что наступили все предшествующие события.

Если А₁,А₂,А₃, … ,А_n– независимые, то формула упрощается следующим образом:

Р(А₁А₂А₃…А_n)= Р(А₁)Р(А₂)…Р(А_n) (5)

Вероятность произведения независимых событий равна произведению вероятностей этих событий.

Теорема сложения вероятностей

несовместных событий

Р(А₁+А₂+А₃+ … +А_n)=Р(А₁)+P(А₂+А₃+ … +А_n)=Р(А₁)+P(А₂)+… +P(А_n)

Вероятность суммы несовместных событий равна сумме вероятностей этих событий.

Теорема сложения вероятностей

совместных событий

Пусть А и В – совместные события, тогда:

Р(А+В)=Р(А)+Р(В)-Р(АВ)

Доказательство:

А наступит тогда и только тогда, когда наступают 2 несовместных события: АВ и А

А=АВ+А

Р(А)=Р(АВ+А)= Р(АВ)+Р(А)

Р(А)= Р(А)-Р(АВ)

В=ВА+В

Р(В)=Р(ВА+В)= Р(ВА)+Р(В)

Р(В)= Р(В)-Р(ВА)

А+В= АВ+А+ ВА+В= АВ+А+В

Р(А+В)=Р(АВ+А+В)= Р(АВ)+р(А)+Р(В)=

= Р(АВ)+ Р(А)-Р(АВ)+ Р(В)-Р(ВА)= Р(А)+ Р(В)-Р(AB)

Обобщение теоремы сложения

Р(А₁+А₂+А₃)= Р(А₁)+Р(А₂+А₃)-Р(А₁[А₂+А₃])=

=Р(А₁)+Р(А₂)+Р(А₃)-Р(А₁А₂) -Р(А₁А₃) -Р(А₂А₃)+Р(А₁А₂А₃) (1)

Если совместны, но независимы nсобытий, то:

А₁+А₂+…+А_nи₁₂…_n– противоположные события.

Р(А₁+А₂+…+А_n)+Р(₁₂…_n)=1

Р(А₁+А₂+…+А_n)=1- Р(₁₂…_n)

Р(А₁+А₂+…+А_n)=1- Р(₁)P(₂)…P(_n) (2)

Пространство элементарных событий

Пространством элементарных событий Ωназывают сумму всех элементарных событий, которые могут наступить в результате опыта.

Элементарное событие– каждый неразложимый исход опыта.

Случайные события можно рассматривать как некоторое множество из соответствующего пространства элементарных событий.

Пример:

Ω :монета

Е₁=[Г,Г] Е₂=[Г,Ц] Е₃=[Ц,Г] Е₄=[Ц,Ц]

Случайные события:

А=Е₃

В=Е₁+Е₂

С=Е₁+Е₃+Е₄

Система событий А₁,А₂,А₃, … ,А_nназываетсяполной, если в результате опыта наступает одно и только одно из этих событий.

(События несовместны, но сумма их – достоверное событие)

Сумма вероятностей полной системы = 1.