16.2.2. Параметры замедляющих систем

Рабочая полоса частот. Поскольку в достаточно добротных резонаторах при одной и той же мощности возбуждения амплитуда колебаний вблизи резонансной частоты резко возрастает, взаимо­действие электронов с СВЧ-полем в замедляющих системах с резонаторами оказывается сильно зависящим от частоты. Иначе го­воря, эти системы относительно узкополосны (в отличие от систем с геометрическим замедлением, образованных линиями передач, не обладающими резонансными свойствами). Однако следует под­черкнуть, что в последних системах полосы пропускания чередуют­ся с полосами запирания, так как изгибы в линиях передачи явля­ются точками нарушения регулярности (точками отражения вол­ны). Если волны, отраженные от последовательных неоднородностей, складываются (когда расстояние между неоднородностями равняется целому числу полуволн в линии), система не пропускает волну. В частном случае спиральных систем, в которых нельзя вы­делить места локализации неоднородностей, запирания не наблю­дается, но вблизи частоты, при которой длина витка спирали рав­няется длине распространяющейся по линии волны (пространст­венный резонанс), наблюдается существенная зависимость фазо­вой скорости волны от частоты.

Таким образом, деление замедляющих систем на два класса с точки зрения их широкополосности в известной степени условно и выбор той или иной системы диктуется рядом других свойств, из ко­торых важнейшим является сопротивление связи .

Сопротивление связи. Параметр подобен эквивалентно­му сопротивлению резонансной электродинамической системыR и так же, как последний, характеризует «способность» системы соз­давать при введении в нее высокочастотной мощности Р СВЧ-напряжение той или иной интенсивности в том месте, где через систе­му проходит электронный поток:

(16.10)

Особенностью замедляющих систем по сравнению с резонато­рами является распределенный вдоль системы характер взаимо­действия, в связи с чем в качестве «продольного» напряжения в (16.10) следует рассматривать линейный интеграл напряженности электрического поля, направленного вдоль осиz (соответст­вующего синусоидальной пространственной гармонике).

Условимся понимать под амплитудой напряжения линейный интеграл продольного электрического поля от точкиz = 0, где на­пряженность продольного поля равна нулю, до точки , т.е. до максимума напряженности поля замедленной волны (здесь, где. Таким образом,

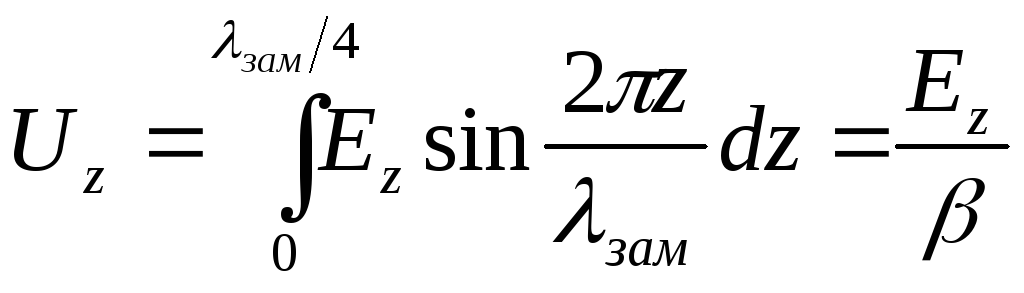(16.11)

где – фазовая постоянная;E_z – амплитуда соответствую­щей пространственной гармоники.

Подставив (16.11) в (16.10), получим выражение для сопротив­ления связи замедляющей системы:

(16.12)

Если сопоставить выражение (16.12) с известным выражением для эквивалентного сбпротивления резонаторов:

(16.12а)

то упоминавшаяся выше аналогия между величинами иR ста­новится особенно наглядной [наличие в знаменателе (16.12) фа­зовой постоянной связано с тем, что в числителе (16.12) стоит не величинаU_z, как в (16.12а), а величина поля E_z, связанная с U_z соотношением (16.11)].

Строгий расчет величины весьма сложен и возможен лишь в простейших случаях. Важную роль в оценках величиныигра­ет эксперимент.

Дисперсия фазовой скорости. Под дисперсией фазовой ско­рости в замедляющих системах понимается ее зависимость от час­тоты. Начнем рассмотрение этого вопроса с системы «встречные штыри», для которой, как уже отмечалось, понятие дисперсии мож­но объяснить весьма наглядно. Прежде всего заметим, что поток в этой системе (как и в некоторых других системах) взаимодействует не со всеми пространственными гармониками. Этот факт можно объяснить следующим образом. Как следует из (16.4), в системе «встречные штыри» время пролета электронов, соответствующее условию синхронизма с нулевой гармоникой (р = 0),

(16.13)

Для взаимодействия с высшими пространственными гармоника­ми (р= ± 1, ± 2 и т.д.) это время должно отличаться от величины, опре­деляемой выражением (16.13), на целое число периодов Т поля:

(16.14)

т.е. условие синхронизма может быть записано в виде

(16.15)

Однако реально взаимодействие электронов с нулевой и ос­тальными четными гармониками в системе «встречные штыри» от­сутствует. Действительно, как видно из рис. 16.2, между ячейками А и В, разделенными периодом L, имеется еще одна ячейка – А'. Обратим внимание на то, что при переходе от ячейки А в соседнюю ячейку А' направление с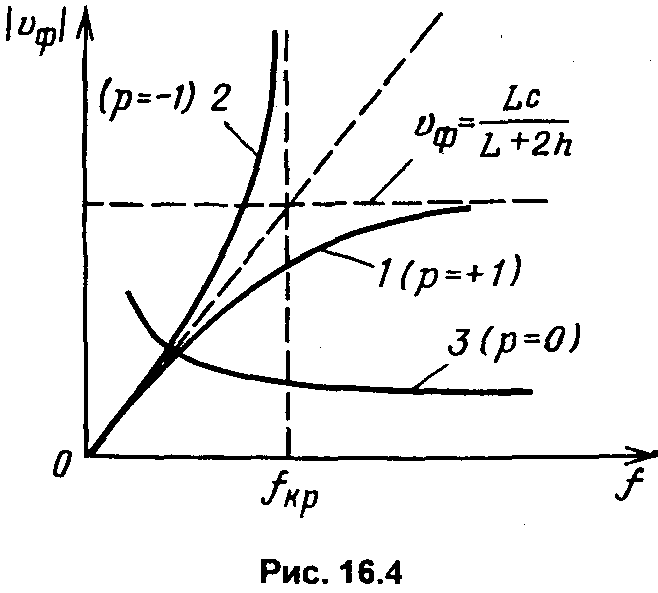иловых линий изменяется на противополо­жное. Это означает, что фаза поля при переходе электрона из ячей­киА в ячейку А' помимо набега фазы на развернутой длине изогну­того участка АА' получает дополнительный сдвиг. Поэтому если обеспечен формальный синхронизм (16.15), электрон, перейдя вдоль осиz из ячейки А в ячейку А' за время , «встретит» в ячейке А' СВЧ-поле противоположной фазы. Соответственно результирующий эффект взаимодействия электрона и поля в двух соседних ячейках рассматриваемой замед­ляющей системы окажется нулевым. Чтобы электрон «встретил» в ячейке А' СВЧ-поле той же фазы, что и в ячейке А, время пролета электронами про­странства между ячейками А и А' должно отличаться от вели­чины на величинуили вообще в силу пери­одичности процесса – на, гдеk=0, 1, 2... Это означает, что в формулах (16.14), (16.15) отличное от ну­ля взаимодействие электронов с СВЧ-полем будет только при нечетных значениях р.

Вернемся к дисперсии. Поскольку с ростом номера гармоник р эффективность взаимодействия потока и поля падает (этот резуль­тат будет прокомментирован ниже), практический интерес предста­вляют гармоники с малыми номерами. При р = 0 принципиально нет взаимодействия, а при р = ±1 из (16.15)

(16.16)

Рассмотрим вначале дисперсионную кривую для прямой гармо­ники, т.е. при р = +1. Из выражения (16.16) следует, что при малых значениях частоты , т.е. рассматриваемая зависимость ли­нейна. Но по мере увеличения частоты f pocт величины замед­ляется; призначениеприближается к постоянной вели­чине (рис. 16.4, кривая1).

Анализ выражения (16.16) показывает, что на низких частотах характер дисперсионных зависимостей для плюс первой и минус первой пространственных гармоник совпадает. Различие начина­ет проявляться по мере увеличения частоты и определяется третьим слагаемым в знаменателе выражения (16.16). С ростом частоты величина этого слагаемого начинает убывать. Однако ес­ли для р = +1 это приводит, как уже отмечалось, к асимптотическо­му приближению дисперсионной кривой к постоянной величине, то для р = –1 фазовая скорость с ростом частоты быстро увеличи­вается. Как видно из (16.16), при некоторой критической частоте f_кр скорость стремится к бесконечно большой величине (см. кривую 2 на рис. 16.4).

Здесь полезно сделать следующее замечание. Система «встречные штыри» образована, как уже отмечалось, волнообраз­ной деформацией двухпроводной линии, которая, как известно, не обладает дисперсией. Вместе с тем рассмотренная выше зависимость величины от частоты определяется только последним слагаемым в знаменателе выражения (16.16), появившимся из (16.15) прир=0. Таким образом очевидно, что наличие дисперсии в замедляющей системе на основе двухпроводной линии связано не с особенностями распространения в такой линии электромаг­нитной волны, а только со спецификой взаимодействия с этой вол­ной потока. В частности, при р = 0 последнее слагаемое в знамена­теле выражения (16.15) оказывается равным нулю и дисперсии нет. Однако, как уже отмечалось, при р = 0 волна и поток в такой ли­нии взаимодействовать не могут; взаимодействие волны и потока имеет место лишь при тех значениях скоростей потока, которые со­ответствуют нечетным значениям числа р. Но именно при р ≠ 0 и наблюдается, как следует из (16.15), (16.16), зависимость скорости от частоты, т.е. дисперсия.

Известно, что в зависимости от знака производной дисперсия подразделяется на нормальную(< 0) и аномаль­ную (> 0). В соответствии с этой классификацией диспер­сия системы «встречные штыри» является, как видно из рис. 16.4, аномальной.

Иной характер имеет дисперсионная характеристика для спи­ральной замедляющей системы. Из рис. 16.4, на котором приве­дена качественная зависимость скорости в такой системе от частоты (кривая 3), видно, что дисперсия спиральной системы яв­ляется нормальной и характеризуется широким бесдисперсионным участком, т.е. областью частот, в пределах которой фазовая скорость от частоты практически не зависит. Отметим также дру­гое отличие от системы «встречные штыри»: в спиральной замед­ляющей системе поток взаимодействует с волной и на четных гар­мониках. Но лампы бегущей волны (ЛБВ) со спиральными замед­ляющими системами работают, как правило, на основной гармо­нике, т.е. при р =0.

В заключение еще раз подчеркнем, что характер дисперсион­ных зависимостей для различных замедляющих систем различен. Но общей закономерностью является принципиально аномаль­ный характер дисперсии для отрицательных пространственных гармоник. Отметим также, что в ряде случаев дисперсионные ха­рактеристики удобно рассматривать в других координатах – на­пример, рассматривается зависимость коэффициента замедле­ния п от длины волны в свободном пространстве или зависимость волнового числа в свободном пространстве k = от фазовой по­стояннойсистемы.