5.2. Электрическая модель биполярного транзистора в статическом режиме (модель Эберса - Молла)

Модель основывается на известных уравнениях для токов через переходы в нормальном активном (5.11) и инверсном активном ре­жимах работы БТ:

I_KN = α_NI_ЭN + I_КБО (5.26)

I_ЭI = α_II_KI + I_ЭБО (5.27)

где I_KN, I_ЭN – токи коллектора и эмиттера при нормальном включе­нии БТ (прямое включение эмиттерного перехода, обратное – кол­лекторного); I_ЭI, I_KI – токи эмиттера и коллектора в инверсном вклю­чении БТ (прямое включение коллекторного перехода, обратное – эмиттерного); α_N, α_I – коэффициенты передачи тока эмиттера и кол­лектора при нормальном и инверсных включениях; I_КБО, I_ЭБО – на­чальные токи коллектора (при I_ЭN = 0) и эмиттера (при I_KN = 0)

Уравнения (5.26) и (5.27) отражают важнейшую особенность БТ: инжектированный любым переходом носитель, пройдя через базовую область, проходит через другой переход при любом зна­ке напряжения на последнем. Другими словами, переходы не представляют барьера для подходящих к ним неосновных носи­телей базовой области, т.е. обеспечивается взаимодействие обоих переходов.

Это дало основание Эберсу и Моллу использовать принцип су­перпозиции и рассматривать токи эмиттера и коллектора как сумму двух составляющих. При этом одна составляющая каждого тока за­висит от напряжения на эмитгерном переходе, а вторая – от напря­жения на коллекторном переходе

На рис. 5.11,а показана модель Эберса-Молла для БТ типа р-n-р, а рис. 5.11,б поясняет связь элементов модели со структурой транзистора. Штриховой линией на рис. 5.11,б выделена основная (идеализированная) часть модели, которая содержит два диода и два зависимых источника тока. Точками Э, Б, К отмечены выводы электродов реального БТ – эмиттера, базы и коллектора, а Э', Б' К' – «внутренние» точки идеализированного БТ. Между точками Э и Э' изображается омическое сопротивление эмиттерной области R_ЭЭ', между К и К' – сопротивление коллекторной области R_KK',а между Б и Б' – сопротивление базовой области для базового тока R_ББ'. Соот­ветственно токи эмиттера I_Э и коллектора I_K протекают через Rээ' и R_KK' и создают на них падение напряжения.

Один диод (D_Э) будем называть эмиттерным диодом, а второй (D_K) – коллекторным. Оба диода в модели включены в прямом на­правлении, так что изображенная модель соответствует режиму насыщения БТ Прямые напряжения на диодах при указанных на рис 5.11 направлениях токов

U_Э’Б’ = U_ЭБ – I_ЭR_ЭЭ’ – I_БR_ББ’ (5.28)

U_К’Б’ = U_КБ + I_KR_KK’ – I_БR_ББ’(5.29)

где U_ЭБ и U_КБ – напряжения источников питания.

Токи диодов I_Э и I_K определяются по известным уравнениям ВАХ:

(5.30)

(5.31)

где I'_ЭО и I'_КО – обратные (тепловые) токи диодов при таких обрат­ных напряжениях U_Э'Б' и U_К'Б', когда | U_Э'Б'| >> m_Эφ_Т, a |U_К'Б'| >> m_Кφ_Т; m_Э и m_К – коэффициенты неидеальности ВАХ диодов (m_Э = 1..2, m_К = 1..2), учитывающие влияние рекомбинационно-генерационных токов в р-n-переходах. В простейшем случае полагают m_Э = m_К = 1 (см. § 3.5.1).

В формулы (5.30) и (5.31) независимо от типа БТ (р-n-р или n-р-n) напряжения подставляются с плюсом при прямом включении пере­хода (диода) и со знаком минус – при обратном. Положительным на­правлением токов диодов считается направление их прямых токов, т.е. от p-области к n-области.

Основная часть прямого тока эмиттерного диода через базу передается в коллектор. Эта часть тока учитывается на рис. 5.11 зависимым генератором тока α_NI'_Э. Аналогично источник тока учи­тывает передачу тока из коллекторного перехода при его прямом включении в эмиттерный переход. Так учитывается равноправность переходов или обратимость биполярного транзистора. Эти токи мо­жно было бы назвать токами связи переходов.

Теперь нужно записать выражения для токов в цепях эмиттера I_Э, коллектора I_К, базы I_Б в соответствии с электрической схемой модели на рис. 5.11,б.

I_Э = I'_Э – α_II'_K (5.32)

I_К = α_N I'_Э – I_К (5.33)

I_Б = I_Э – I_К = (1– α_N) I'_Э – (1– α_I) I_К (5.34)

Используя (5.30) и (5.31), можно записать (5.32), (5.33) и (5.34) в виде

(5.35)

(5.36)

(5.37)

Достоинством этих уравнений Эберса-Молла является то, что одна составляющая каждого тока зависит только от напряжения эмиттерного диода (эмиттерного перехода), а вторая – только от на­пряжения коллекторного диода (коллекторного перехода). Однако пока остается открытым вопрос о нахождении для реального БТ па­раметров модели I′_Э0, I′_К0, m_Э, m_К – параметров «недоступных» дио­дов. Очевидно, что значения этих параметров можно найти только с помощью специальных измерений.

Заметим, что если бы удалось сделать опыт короткого замы­кания коллекторного диода U_К′Б′ = 0, то вторые слагаемые в (5.35), (5.36) и (5.37) обратились бы в нуль. Тогда эксперимен­тальное исследование первых слагаемых позволило бы опреде­лить искомые параметры I′_Э0 и m_Э. Аналогично при U_Э′Б′ = 0 исчез­нут первые слагаемые и в результате экспериментального ис­следования оставшихся вторых слагаемых можно было бы найти I′ко и т_к. Но осуществлению U_К′Б′ = 0 и U_Э′Б′ = 0 мешает наличие сопротивлений модели Rээ', R_ББ', R_KK', отделяющих диоды от внешних выводов транзисторов.

Проведенные рассуждения позволяют раскрыть физический смысл токов I′_Э0, I′_К0- это обратные токи диодов в условиях, ког­да другой диод закорочен. Следует отметить, что есть модифи­кации модели, в которых для определения указанных парамет­ров используются опыты короткого замыкания на внешних выво­дах БТ (U_КБ = 0 и U_ЭБ = 0).

Наиболее распространена методика определения параметров модели Эберса-Молла по измерениям зависимостей I_К = f(U_КБ) в активном инверсном режиме работы и I_Э= f(U_ЭБ) в активном нор­мальном режиме работы БТ.

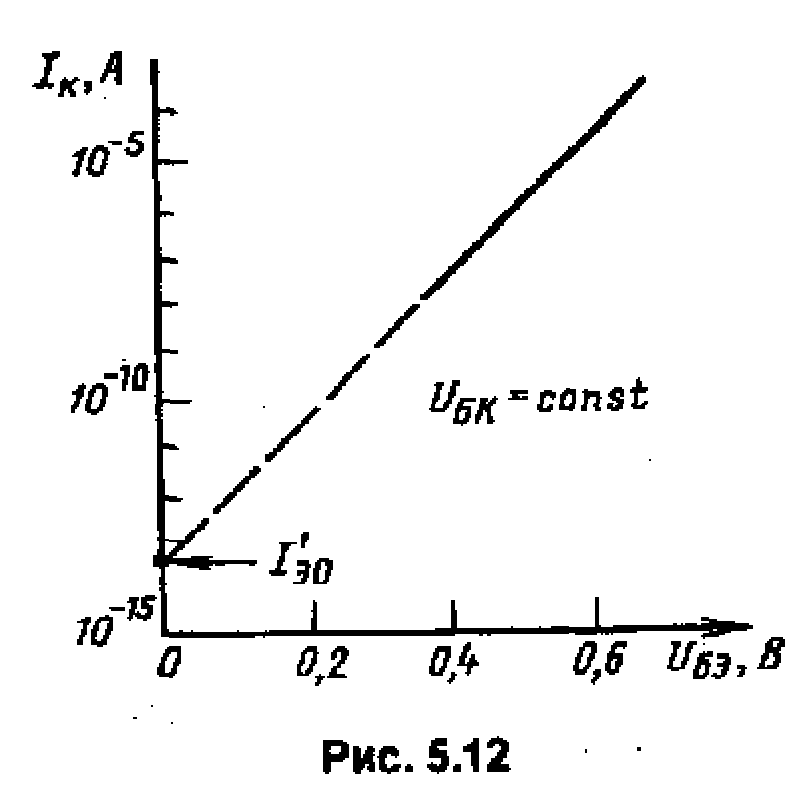Для определения I′_Э0 снимают зависимость I_К = f(U_ЭБ) при U_КБ = const в нормальном активном режиме, но при |U_КБ|>>φ_Т. Зависи­мость строят в полулогарифмическом масштабе, как показано на рис. 5.12. При U_ЭБ >> φ_Т и | U_КБ|>>φ_Т эта зависимость представляет­ся прямой линией, а значением второго слагаемого в (5.36) можно пренебречь. Выражение для I_К на этом участке можно представить первым слагаемым в (5.36):

Продолжив эту прямую линию до пе­ресечения с осью томов (U_ЭБ = 0), по­лучим I^*_К = α_NI′_Э0. Значение параме­тра модели I′_Э0 = I^*_К /α_N ≈ I^*_К. Соот­ветственно угол наклона прямой линии определяет значение m_Э φ_Т, а следовательно, и коэффициент неидеальности m_Э.

Обычно утверждают, что для модели Эберса-Молла характерно условие обратимости

α_I I′_К0 = α_NI′_Э0(5.38)

т.е. независимыми могут быть только три параметра из четырех. Этим можно воспользоваться при определении параметров по результатам измерений.Например, если известно α_N, α_I, I′_Э0 мо­жно вычислить. Однако при записи (5.38) не обсуждается сте­пень применимости этого условия к реальным БТ в различных ре­жимах работы.

Решая совместно (5.35) и (5.36), можно связать параметры мо­дели I′_Э0 и I′_К0 с паспортными параметрами БТ и I_ЭБО и I_КБО. Ток I_ЭБО – это обратный ток эмиттера в активном режиме при обрыве цепи кол­лектора (I_К = 0), а I_КБО – обратный ток коллектора в нормальном ак­тивном режиме при I_Э = 0:

I′_Э0 = I_ЭБО/(1– α_Iα_N); I′_К0= I_КБО/(1– α_Iα_N)

Поэтому часто уравнения (5.35 – 5.37) записываются в виде

(5.40)

Если из схемы на рис. 5.11,а исключить последовательные со­противления областей Rээ', R_ББ', R_KK', то получится основная (простейшая) модель Эберса-Молла. В этой модели напряжения на дио­дах равны напряжениям внешних источников питания.

В усложненных моделях кроме сопротивлений областей для повышения точности модели следует учитывать эффект Эрли (см. § 5.1.3). Для учета этого эффекта, приводящего к появлению наклона выходных характеристик в нормальном активном режи­ме, можно между точками К' и Э' включить зависимый генератор тока (U_К'Э'/U_А)I'_Э, где U_А – параметр, называемый напряжением Эрли. Чем меньше выходная характеристика отклоняется от гори­зонтальной прямой, тем больше напряжение U_А. Иногда вместо генератора тока включают резистор, сопротивление которого оп­ределяется наклоном выходной характеристики.

Дальнейшее уточнение модели может быть достигнуто вве­дением, параметров, учитывающих зависимость коэффициен­тов передачи токов α_N, α_I от величины выходного тока и темпе­ратуры. Однако уточнения модели приводят к увеличению чис­ла параметров, используемых для описания модели. Наиболее сложными являются модели, предназначенные для автомати­зированного проектирования транзисторов и схем на их осно­ве. В качестве примера отметим модель Гуммеля-Пуна [4]. В ней учитываются: снижение коэффициента передачи при боль­ших токах; эффект Эрли введением напряжения Эрли как для нормального активного режима, так и для инверсного; рекомбинационный ток эмиттерного перехода при малых прямых на­пряжениях эмиттер – база.