
- •Глава 5 биполярные транзисторы
- •5.1. Принцип действия биполярного транзистора. Режимы работы
- •5.1.1. Общие сведения
- •5.1.2. Физические процессы в бездрейфовом биполярном транзисторе
- •5.1.3. Влияние режимов работы бт на токи электродов
- •5.2. Электрическая модель биполярного транзистора в статическом режиме (модель Эберса - Молла)
- •5.3. Статические характеристики биполярных транзисторов
- •5.3.1. Схема с общей базой
- •5.3.2. Схема с общим эмиттером
- •5.3.3. Влияние температуры на статические характеристики бт
- •5.3.4. Зависимость коэффициентов передачи тока от электрического режима работы бт
- •5.4. Дифференциальные параметры биполярного транзистора в статическом режиме
- •5.5. Квазистатический режим биполярного транзистора в усилительном каскаде
- •5.5.1. Графоаналитическое рассмотрение при большом сигнале
- •5.5.2. Биполярный транзистор в квазистатическом режиме как линейный четырехполюсник
- •5.6. Нелинейная и линейная динамические модели биполярного транзистора
- •5.6.1. Нелинейная динамическая модель биполярного транзистора
- •5.6.2. Линейная (малосигнальная) модель биполярного транзистора
- •5.7. Частотные свойства биполярного транзистора
- •5.7.1. Постановка задачи
- •5.7.2. Зависимость коэффициента инжекции
- •5.7.3. Зависимость коэффициента переноса от частоты
- •5.7.4. Частотная зависимость эффективности коллекторного перехода
- •5.7.5. Частотная зависимость коэффициента передачи тока в схеме с общей базой
- •5.7.6. Частотная зависимость коэффициента передачи тока в схеме с общим эмиттером
- •5.7.7. Способы улучшения частотных свойств биполярных транзисторов
- •5.8. Переходные процессы в биполярном транзисторе и простейшем ключе на его основе
- •5.8.1. Переходные процессы в биполярном транзисторе при скачке входного тока
- •В установившемся режиме
- •5.8.2. Статический режим ключевой схемы на биполярном транзисторе
- •5.8.3. Переходные процессы в простейшем ключе в схеме с оэ
- •5.9. Шумы биполярных транзисторов
5.1.3. Влияние режимов работы бт на токи электродов
Связь коллекторного и эмиттерного переходов обеспечивается базовой областью, т.е. зависит от характера движения носителей в этой области. В бездрейфовом БТ оно имеет диффузионный характер, т.е. определяется градиентом концентрации носителей в базе, а в дрейфовом БТ зависит еще от имеющегося в базе электрического поля. Таким образом, влияние режимов работы (напряжений переходов) на токи в значительной мере определяется изменением закона распределения концентрации носителей в базовой области от эмиттера к коллектору.
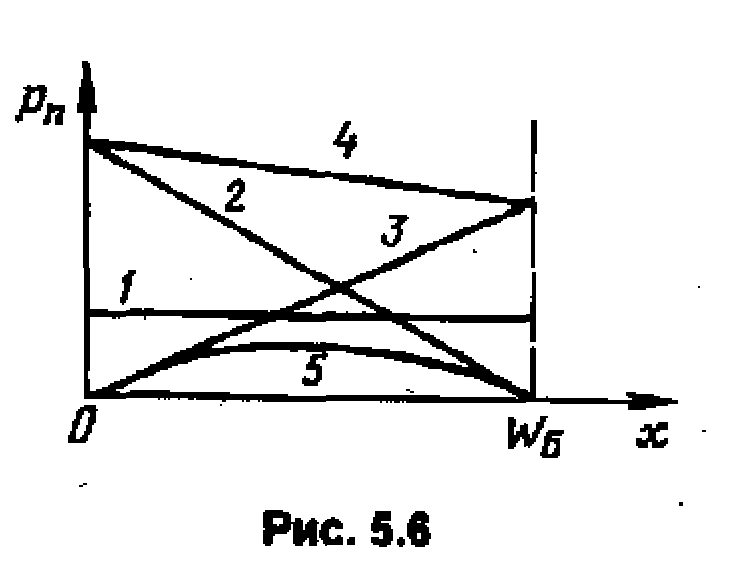 Бездрейфовый
транзистор. На рис. 5.6
показано распределение концентрации
носителей в базе бездрейфового БТ. Левая
граница базы соответствует х
= 0, а правая – х
= WБ.
В состоянии равновесия БТ UЭБ
= UКБ
= 0. Прямая 1
соответствует равновесной концентрации
неосновных носителей.В
нормальном активном режиме прямое
напряжение на эмиттерном переходе
вызывает появление избыточных носителей
ризб(0)
> 0, а обратное
напряжение на коллекторном переходе –
уменьшение концентрации по сравнению
с равновесным значением. Это изменение
тоже можно назвать избыточной
концентрацией, если приписать ей
отрицательный знак (pизб(WБ)
< 0). Расчет (см. § 3.4)
показывает, что при абсолютном
значении обратного напряжения |Uкб|
> 3 φТ
= 0,075 В концентрация
неосновных носителей около коллекторного
перехода практически падает до нуля,
а точнее до значения, которое должно
обеспечивать ток через переход. Это
отражает тот физический факт, что все
подошедшие к коллекторному переходу
неосновные носители захватываются
ускоряющим полем перехода и переносятся
в коллекторную область. Распределение
концентрации в базе (кривая 2) отражает
наличие градиента концентрации, который
определяет направление диффузионного
движения носителей от эмиттера к
коллектору.
Бездрейфовый
транзистор. На рис. 5.6
показано распределение концентрации
носителей в базе бездрейфового БТ. Левая
граница базы соответствует х
= 0, а правая – х
= WБ.
В состоянии равновесия БТ UЭБ
= UКБ
= 0. Прямая 1
соответствует равновесной концентрации
неосновных носителей.В
нормальном активном режиме прямое
напряжение на эмиттерном переходе
вызывает появление избыточных носителей
ризб(0)
> 0, а обратное
напряжение на коллекторном переходе –
уменьшение концентрации по сравнению
с равновесным значением. Это изменение
тоже можно назвать избыточной
концентрацией, если приписать ей
отрицательный знак (pизб(WБ)
< 0). Расчет (см. § 3.4)
показывает, что при абсолютном
значении обратного напряжения |Uкб|
> 3 φТ
= 0,075 В концентрация
неосновных носителей около коллекторного
перехода практически падает до нуля,
а точнее до значения, которое должно
обеспечивать ток через переход. Это
отражает тот физический факт, что все
подошедшие к коллекторному переходу
неосновные носители захватываются
ускоряющим полем перехода и переносятся
в коллекторную область. Распределение
концентрации в базе (кривая 2) отражает
наличие градиента концентрации, который
определяет направление диффузионного
движения носителей от эмиттера к
коллектору.
Плотность диффузионного дырочного тока в базе в произвольном сечении х
jp(x)=qDpdp(x)/dx(5.23)
Если потери на рекомбинацию в базе пренебрежимо малы, то плотность тока jр от координаты не зависит и остается постоянной. Но это предположение означает, что dp/dx = const, т.е. распределение р(х) прямолинейное. Потеря носителей из-за рекомбинации означает уменьшение плотности тока, уменьшение производной и, следовательно, отклонение распределения концентрации от прямолинейного вниз. Это отклонение при коэффициенте переноса, близком к единице (æБ ≈ 1), на рис. 5.5 в одном масштабе изобразить невозможно, но принципиально оно существует.
В инверсном активном режиме (ИАР) переходы БТ поменялись ролями и распределение р(х)изображается прямой 3 (почти прямой). В режиме насыщения (РН), когда оба перехода включены в прямом направлении, концентрации у границ обоих переходов выше равновесного значения, так что распределениер(х) изображается прямой 4. Это распределение можно представить как сумму распределений 2 и 3 нормального и инверсного режимов, что и будет потом использовано для получения электрической модели БТ. Наконец, в режиме отсечки (обратные напряжения на обоих переходах) концентрации у границ переходов практически равны нулю, а в базовой области ниже равновесного значения (кривая 5). Градиенты у границ переходов определяют величину токов переходовIКБ0иIЭБ0.
Знание характера распределения концентрации носителей позволяет наглядно представить влияние напряжений на переходах IЭБ и IКБ на токи электродов IЭ, IК и ток базы IБ = IЭ – IК. Однако приведенное рассмотрение идеализированное, так как неявно предполагалась в тексте и на рис. 5.6 независимость ширины базовой областиWб от напряжений переходов.
В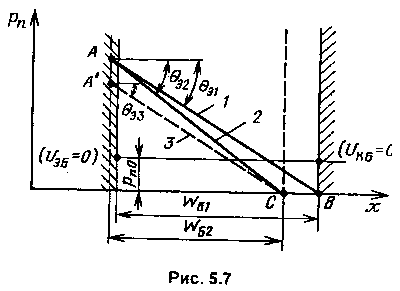 реальном БТ изменение напряжений на
переходахUЭБ
и UКБ
вызывает изменение
толщины обедненных слоев перехода и
смещение границ базовой области,
т.е. изменение ширины базовой области.
Это явление называютэффектом
Эрли.Особенно заметно изменение
ширины базы при подаче обратных напряжений
на переходы. В нормальном активном
режиме, когда на эмиттерном переходе
прямое напряжение, а на коллекторном
обратное и сравнительно большое по
величине, толщина коллекторного перехода
значительно больше, чем эмиттерного,
и влиянием смещения границы эмиттерного
перехода можно пренебречь.Поэтому
увеличение (по модулю) обратного
напряжения UКБ
будет приводить к расширению коллекторного
перехода и сужению базовой области.
реальном БТ изменение напряжений на
переходахUЭБ
и UКБ
вызывает изменение
толщины обедненных слоев перехода и
смещение границ базовой области,
т.е. изменение ширины базовой области.
Это явление называютэффектом
Эрли.Особенно заметно изменение
ширины базы при подаче обратных напряжений
на переходы. В нормальном активном
режиме, когда на эмиттерном переходе
прямое напряжение, а на коллекторном
обратное и сравнительно большое по
величине, толщина коллекторного перехода
значительно больше, чем эмиттерного,
и влиянием смещения границы эмиттерного
перехода можно пренебречь.Поэтому
увеличение (по модулю) обратного
напряжения UКБ
будет приводить к расширению коллекторного
перехода и сужению базовой области.
К каким же последствиям может привести эффект Эрли? Для определенности рассмотрим увеличение обратного напряжения UКБ, приводящее к уменьшению ширины базовой области WБ.
1. Уменьшение WБ вызовет рост градиента концентрации неосновных носителей в базе и, следовательно, рост тока эмиттера. На рис. 5.7 увеличение модуля |UКБ|от |UКБ1|до |UКБ1|при постоянном (заданном) напряженииUЭБ соответствует переходу от распределения 1 к распределению2. Так как θЭ2 > θЭ1 (увеличение градиента), то IЭ2 > IЭ1.
2. В ряде случаев при изменении UКБ требуется сохранить ток эмиттера. Чтобы вернуть IЭ от значения IЭ2 к значению IЭ1, необходимо уменьшить напряжение на эмиттерном переходе до значения, при котором градиент вернется к исходному значению (θЭ3 = θЭ1), а распределение изобразится прямой 3 (A'C), параллельной прямой АБ.
3. Уменьшение WБприведет также к росту коэффициента переноса æБв базе. В случае поддержания постоянства тока эмиттера это будет сопровождаться уменьшением тока базыIБ.Однако можно доказать, что IБ также уменьшится, но в меньшей мере, если IЭ не возвратится к исходному значению.
4. Увеличение коэффициента переноса при уменьшении WБ означает некоторый рост статических коэффициентов передачи α и β.
5. Рост α и IЭ при уменьшении WБ приведет к увеличению коллекторного тока (5.11): IК = α IЭ + IКБО. Так как α ≈ 1 и его рост относительно мал, даже если он достигнет предельного значения (α = 1), то основное влияние окажет рост IЭ.
6. В ряде случаев требуется при уменьшении ширины базы из-за эффекта Эрли сохранять неизменным ток базы. Для компенсации произошедшего уменьшения IБ необходимо дополнительно увеличить IЭ (т.е. общий поток инжектированных в базу носителей) в соответствии с формулой (5.17):
IБ = (1–α)IЭ –IКБ0
Дрейфовый транзистор. В дрейфовом БТ из-за наличия электрического поля в базе EБ ток инжектированных носителей (дырок в р-n-р-транзисторе) состоит из диффузионной и дрейфовой составляющих:
IЭp (x)=SЭ q Dp dpБ / dx+SЭ q μp pБ(x )EБ (5.24)
Вследствие малости потерь в базе из-за рекомбинации суммарный ток IЭp практически остается постоянным (не зависит от координаты), т.е. IЭp (x) = const. Однако соотношение составляющих не остается неизменным. Поясним этот вывод.
Коллекторный переход по-прежнему производит экстракцию неосновных носителей из базы, поэтому их концентрация у коллекторного перехода (x =WБ) очень мала и практически равна нулю (рБ(WБ)≈ 0). У этой границы базовой области дрейфовой составляющей тока можно пренебречь. Градиент концентрации приx =WБможно вычислить из (5.24), считаярБ(WБ)≈ 0:
dpБ(WБ)/dx= IЭp /SЭ qDp (5.25)
Однако у границы базы с эмиттерным переходом (х = 0) из-за увеличения рБ(WБ) обе составляющие в (5.24) становятся соизмеримыми. Поэтому при постоянстве IЭp вычисленное по формуле (5.23) значение градиента при х = 0 должно быть меньше, чем при x = WБ no формуле (5.25). Таким образом, в отличие от бездрейфового БТ распределение рБ(x) в дрейфовом БТ должно быть выпуклым (рис. 5.8).
Очевидно, чем больше напряженность внутреннего поля в базе EБ, тем меньше градиент концентрации в начале базовой области и меньше вклад в полный ток диффузионной составляющей тока в этой части базы.
Следует
обратить внимание на то, что распределение
концентр ации
в инверсном активном режиме для дрейфового
БТ качественно отличается от распределения
в нормальном активном режиме.
Объясняется это тем, что внутреннее
поле для дырок, инжектируемых из
коллектора в базу, является тормозящим.
а не ускоряющим, как в нормальном активном
режиме для дырок, инжектируемых из
эмиттера в базу. Поэтому криваярБ(x)
будет не выпуклой, а вогнутой, а значения
концентрации увеличатся в несколько
раз (рис. 5.9).
ации
в инверсном активном режиме для дрейфового
БТ качественно отличается от распределения
в нормальном активном режиме.
Объясняется это тем, что внутреннее
поле для дырок, инжектируемых из
коллектора в базу, является тормозящим.
а не ускоряющим, как в нормальном активном
режиме для дырок, инжектируемых из
эмиттера в базу. Поэтому криваярБ(x)
будет не выпуклой, а вогнутой, а значения
концентрации увеличатся в несколько
раз (рис. 5.9).
Р аспределение
концентрации в базе в режиме насыщения
(двухсторонней инжекции) можно приближенно
представить как сумму распределений
при нормальном и инверсном режимах. При
этом вид распределения и результирующий
избыточный заряд близки к инверсному
режиму в отличие от бездрейфового БТ,
где оно имеет вид трапеции (рис. 5.10).
аспределение
концентрации в базе в режиме насыщения
(двухсторонней инжекции) можно приближенно
представить как сумму распределений
при нормальном и инверсном режимах. При
этом вид распределения и результирующий
избыточный заряд близки к инверсному
режиму в отличие от бездрейфового БТ,
где оно имеет вид трапеции (рис. 5.10).
