5.7.5. Частотная зависимость коэффициента передачи тока в схеме с общей базой

Подставив (5.92), (5.96) и (5.108) в выражение (5.84), получим

(5.109)

где α_N = γ_Эæ_БМ_К – коэффициент передачи при f → 0, т.е. на очень ни­зких частотах или в статическом режиме.

В рабочей области частот сигнала справедливы условия

f / f_Э<< 1; f / f_Б << 1; f / f_К << 1; f / f_{К пр} << 1 (5.110)

Поэтому, производя перемножение в знаменателе (5.109) и пренебрегая слагаемыми второго порядка малости, получаем

(5.111)

Введем обозначения

(5.112)

и приведем (5.111) к простому виду

(5.113)

Частотная зависимость модуля коэффициента передачи в схе­ме с ОБ (управление по эмиттеру)

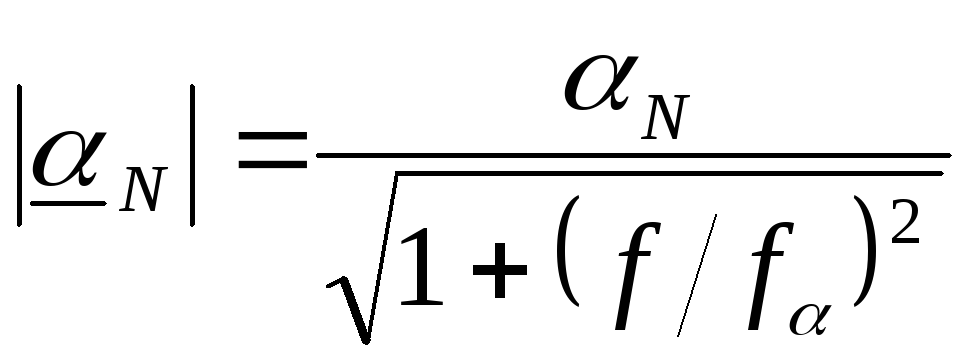, (5.113а)

где f_α – предельная частота коэффициента передачи в схеме с ОБ (другое обозначение f_h21Б). При f =f_α (рис. 5.30). Подставив (5.91), (5.97), (5.105) и (5.107) в (5.112), получим

, (5.114)

или с учетом (5.99) и (5.104)

1/f_α = 2π[r_ЭС_Эб + r_ЭС_Эдф + (R_ББ' + R_КК' )С_Кб + t_{К пр}/2] (5.115)

Сумма в скобках выражения (5.114) характеризует полную инер­ционность БТ. Ее часто называют полной временной задержкой сиг­нала от эмиттера до коллектора и обозначают через τ_эк:

τ_ЭК =τ_Э + t_{Б np}+ τ_к + t_{К пр}/2. (5.116)

Тогда вместо (5.114) можно записать

f_α = 1/2π τ_ЭК. (5.117)

5.7.6. Частотная зависимость коэффициента передачи тока в схеме с общим эмиттером

Коэффициенты передачи в статическом режиме схем с ОБ и ОЭ связаны соотношением

β_N = α_N /(1– α_N). (5.118)

Так как первый закон Кирхгофа справедлив и для переменных со­ставляющих в общей точке, то характер связи (5.118) сохраняется в динамическом режиме, т.е.

β_N = α_N /(1– α_N). (5.119)

Подставив в (5.119) выражение (5.113) и произведя несколько не­сложных преобразований,получим

β_N = β_N / (1+ j(f / f_β)), (5.120)

гдеf_β =(1– α_N)f_α = f_α /( β_N +1) ≈ f_α / β_N (5.121)

Соответственно модуль из (5.120)

|β_N| = β_N / (1+ j(f / f_β)²)^1/2

Характеристическая частота, при которой модуль |β_N| уменьшает­ся до значения β_N / √2 , называется предельной частотой коэффи­циента передачи в схеме с ОЭ. Другое обозначение ее f_h21Э. Так как f_β ≈ f_α / β_N, тo говорят, что частотные свойства схемы с ОЭ много хуже, чем схемы с ОБ. Выигрыш в значении коэффициента передачи (β_N >> α_N) coпровождается проигрышем в частотных свойствах. Сравнение зави­симостей |β_N| и |α_N| от частоты показано на рис. 5.30.

Очень часто различную зависимость от частоты β_N и α_N в схемах с ОБ и ОЭ поясняют с помощью векторной диаграммы БТ в динамичес­ком режиме (рис. 5.31,а). На ней изображены векторы токов эмиттера İ_Э, коллектора İ_К и базы İ_Б, которые отображают физические процес­сы в БТ и формально первый закон Кирхгофа в обшей точке:

İ_Э+ İ_К + İ_Б =0 (5.122)

коэффициенты передачи в схемах с ОБ и ОЭ можно записать как

α_N = İ_К / İ_Э; β_N = İ_К / İ_Б (5.123)

Обычно говорят, что с ростом частоты при том же времени про­лета в базе увеличивается фазовый угол сдвига φ (запаздывание) коллекторного тока относительно эмиттерного İ_Э. Пока частота сиг­нала f < f_α модуль | İ_К | мало изменяется, поэтому рост частоты и угла φ должен приводить к сильному росту İ_Б, чтобы выполнялся первый закон Кирхгофа (5.122). А это значит, что модуль|β_N| должен сильно уменьшаться, т.е. зависимость коэффициента передачи в схеме с ОЭ от частоты более сильная, чем в схеме с ОБ. Это действительно так, но пока нет объяснений физической причины увеличения тока базы с ростом частоты. Как понять этот рост, если ток базы связан обычно с потерями на рекомбинацию в базе, а время пролета в ней остается тем же и не зависит от частоты?

В действительности большой рост İ_Б необходимо связывать не с потерями на рекомбинацию, а с диффузионной емкостью. В дина­мическом режиме при частоте f необходимо f раз в секунду произ­водить нейтрализацию заряда инжектированных носителей в базу. Этот процесс характеризуется диффузионной емкостью

С_{Э дф} = dQ_изб / dU_ЭБ

Соответственно емкостный ток, необходимый для нейтрализа­ции базы при синусоидальном напряжении равен

I_{Б нейтр} = С_{Э дф} dU_ЭБ / dt = ωС_{Э дф} U_{ЭБ m} cos ωt

Отсюда следует, что базовый ток в динамическом режиме ли­нейно зависит от частоты и может многократно превышать потери на рекомбинацию.

Для характеристики частотных свойств БТ широко использу­ется так называемая граничная частота f_гр (или f_T), на которой модуль |β_N| = 1. Очевидно, что Поэтому вместо (5.121) при условииf >3f_βможно записать

| β_N (f)| = β_N/ (f / f_β)

или

| β_N (f)| f= f_ββ_N= const (5.124)

т.е. зависимость становится гиперболической. На граничной частоте

| β_N (f_гр)| f_гр= f_ββ_N(5.124а)

Так как

| β_N (f_гр)| = 1,

то

f_гр = f_β β_N (5.125)

Но (5.124) можно переписать с учетом (5.125) в виде

| β_N (f)| f = f_гр (5.126)

Таким образом, если взята произвольная частота f > 3 f_β и известен на ней модуль коэффициента передачи | β_N (f)|, то их произведение дает значение граничной частоты.

Граничная частота несколько меньше предельной частоты f_α в схеме с ОБ, но для практических оценок их можно считать равными.