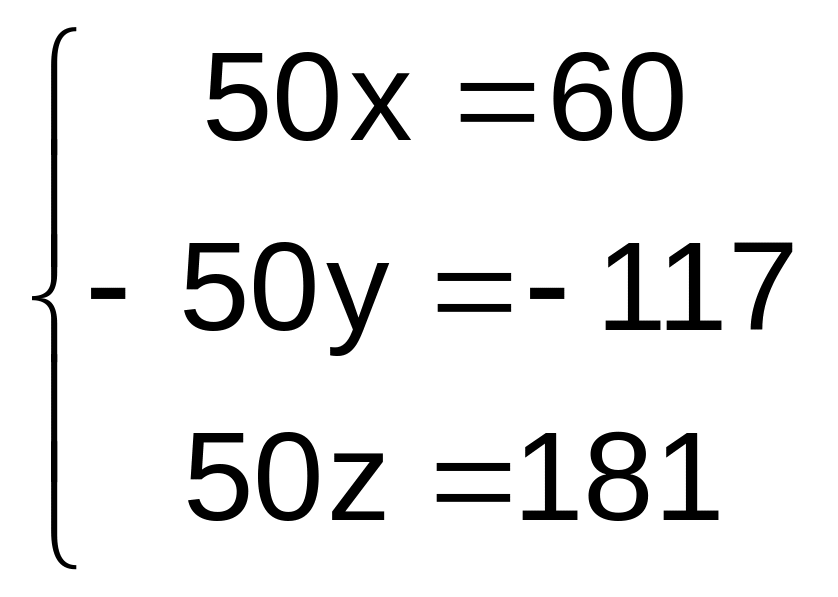Мопред - возвращает определитель матрицы (матрица хранится в массиве). Синтаксис функции: мопред(массив).

Решение системы линейных уравнений методом прогонки (в Excel).

Рассмотрим следующую систему n линейных уравнений:

.

Найдем решение этой системы методом прогонки. По формулам прямого хода определяем _i, _i. Затем по формулам обратного хода определяем y_i для i = n, n-1,... 1.

Задание 3: Итак, в Excel организуем таблицу:

a	c	b	f	альфа	бета	y
	2	1	4	0,5	2
	[…]	[…]	[…]	[…]	[…]

в которой задаем коэффициенты исходной системы уравнений, потом по рекуррентным формулам из лекций находим _i, _i и, начиная с последнего, находим значения искомых переменных y_i.

Решение систем линейных уравнений в MathCad

Для решения СЛУ в MathCAD есть встроенная функция lsolve(А, b). Встроенную функцию lsolve допускается применять и при символьном решении СЛУ. Функция rref(А’) позволяет привести расширенную матрицу системы А’ к верхнему треугольному виду и, тем самым, позволяет решить СЛУ методом Гаусса.

Задание 4: Решите при помощи функции lsolve (А, b) систему уравнений из задания 1.

Задание 5: Задайте А’ расширенную матрицу изучаемой системы уравнений. Проверьте, чему равен её ранг. Приведите ее к треугольному виду, после чего найдите значения переменных.

Часть 2. Решение систем нелинейных уравнений Изучение алгоритмов численного решения систем нелинейных уравнений в Excel

1. Метод простой итерации.

Рассмотрим систему алгебраических нелинейных уравнений:

.

Судя по коэффициентам, в этой системе нелинейная часть дает лишь относительно малый вклад, поэтому попробуем решить её методом простых итераций. За первое приближение примем решение системы линейных уравнений, получаемых отбрасыванием нелинейной части. Значения переменных на следующем шаге можно выразить в виде X=S(X) следующим образом:

О точности полученных значений можно судить, например, по расстоянию |Х^k+1 - Х^k| между решениями, найденными на данном и предыдущем шагах итерации. В данной задаче вектор Х имеет три координаты: x, y и z.

Задание 6: Решите данную систему нелинейных уравнений методом простой итерации. Для этого организуйте таблицу

x	y	z	∆X
[…]	[…]	[…]	[…]

Значения первого приближения найдите любым из изученных вами методов решения систем линейных уравнений. Расчет закончите при ∆Х = |Х^k+1 - Х^k |< 0,001. Запомните количество итераций, необходимое для выполнения искомой точности, и полученные значения корней. Посмотрите, сходится ли данный метод, если за первое приближение принять первые попавшиеся значения или решения совсем уж упрощенной системы: