Кут між двома прямими

А₁х+В₁у+С₁=0 і А₂х+В₂у+С₂=0, то кут між прямими дорівнює куту між їх нормальними векторами N₁ = (A₁; B₁) і N₂ = (A₂; B₂) як кути із взаємно перпендикулярними сторонами. Отже, шуканий кут j визначається за формулою:

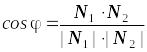= . Без точки С

Умовою паралельності прямих є рівність 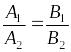, умовою перпендикулярності двох прямих є рівність А₁А₂ +В₁В₂ =0.

також .

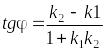Дві прямі паралельні тоді і тільки тоді, коли їх кутові коефіцієнти рівні, тобто k₁= k₂.

Дві прямі перпендикулярні тоді і тільки тоді, коли їх кутові коефіцієнти задовольняють умову 1+k₁k₂=0, тобто k₂= –1/k₁.

Відстань від точки до прямої

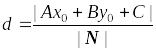або

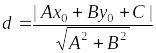
10 .

Векторне і загальне рівняння площини

В координатній формі це рівняння запишеться так:

А(x–х₀)+В(у–у₀)+С(z–z₀)=0.

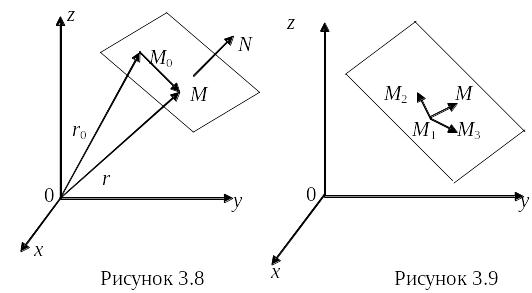
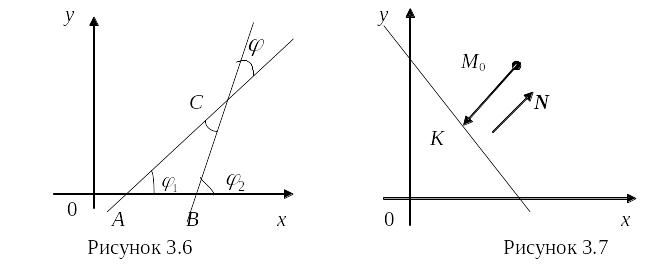
Положення площини відносно прямокутної системи координат Охуz повністю визначається деякою точкою М₀(х₀; у₀; z₀) на площині і вектором N, який перпендикулярний до цієї площини. Вектор N, перпендикулярний до площини, називається нормальним вектором площини.

якщо вектор N = (A, B, C) є нормальним вектором площини, то її рівняння має вигляд Aх +By+Cz+D = 0.

Кут між площинами.

Умови паралельності і перпендикулярності двох площин.

А₁x+В₁y+С₁z+D₁=0 і А₂x+В₂y+С₂z+D₂=0. Знайдемо кут φ між цими площинами. Цей двогранний кут, що утворюється цими площинами, вимірюється лінійним кутом φ, що дорівнює куту між нормальними векторами N₁=(A₁, B₁, C₁) і N₂=(A₂, B₂, C₂) як кути з відповідно перпендикулярними сторонами, який знайдемо за формулою

cosφ= = .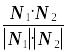

Якщо дві площини паралельні, то їх нормальні вектори колінеарні, а тому їх координати пропорційні .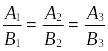

Якщо дві площини перпендикулярні, то N₁ ^ N₂ і дістанемо умову перпендикулярності двох площин:

A₁A₂+B₁B₂+C₁C₂ = 0.

Кут між двома прямими

А₁х+В₁у+С₁=0 і А₂х+В₂у+С₂=0, то кут між прямими дорівнює куту між їх нормальними векторами N₁ = (A₁; B₁) і N₂ = (A₂; B₂) як кути із взаємно перпендикулярними сторонами. Отже, шуканий кут j визначається за формулою:

=

Умовою паралельності прямих є рівність , умовою перпендикулярності двох прямих є рівність А₁А₂ +В₁В₂ =0.

також формула кута .

Дві прямі паралельні тоді і тільки тоді, коли їх кутові коефіцієнти рівні, тобто k₁= k₂.

Дві прямі перпендикулярні тоді і тільки тоді, коли їх кутові коефіцієнти задовольняють умову 1+k₁k₂=0, тобто k₂= –1/k₁.

Кут між прямою та площиною

Означення. Кутом між прямою і площиною називається кут між цією прямою і її проекцією на площину

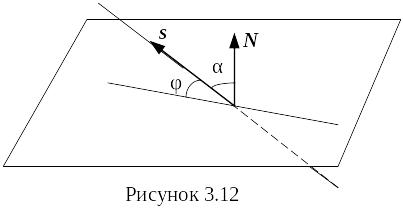
Нехай задана площина загальним рівнянням і пряма канонічними рівняннями

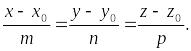
Оскільки нормальний вектор площини N перпендику-лярний до площини, а напрямний вектор прямої s паралельний прямій, то умова перпендикулярності прямої до площини полягає в тому, що N || s, тобто

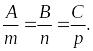
Пряма паралельна площині, якщо N ^ s, тобто коли

Відстань від точки до прямої

або

Відстань від точки до площини

Нехай задана площина своїм загальним рівнянням

=0 і деяка точка поза площиною. Тоді відстань d від цієї точки до площини визначається за формулою

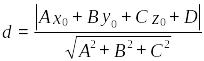. (3.22)

де A, B і C є координатами нормального вектора площини, якщо замість біжучих координат підставити координати даної точки .

11.

Криві другого порядку

Важливим є випадок, коли лінія в декартовій системі координат 0ху описується рівнянням другого степеня з двома змінними, яке в загальному

вигляді можна записати так:

де А, В, С, D, E, F – задані числа, а х і у – змінні.

Такі лінії називаються кривими другого порядку. До них відносяться коло, еліпс, гіпербола і парабола.

1 .Рівняння кола

Н агадаємо, що колом називається множина всіх точок площини, рівновіддалених від даної точки, що називається центром кола. Виберемо

на колі біжучу точку М(х; у). Розглянемо вектор За означенням кола Оскільки

то матимемо

звідки (3.31)

Це і є шукане рівняння кола.

Звернемо увагу на те, що, якщо в рівнянні (3.31) розкрити дужки, то дістанемо рівняння Звідси видно, що старші коефіцієнти (коефіцієнти при других степенях змінних) рівні між собою, відсутній член з добутком змінних координат. Це є ознакою, що рівняння 2-го степеня з двома змінними описує коло.

Еліпс

Означення. Еліпсом називається множина точок площини, сума відстаней яких від двох даних точок цієї самої площини, що називається фокусами еліпса, є величиною сталою і більшою, ніж відстань між фокусами.

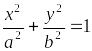. Рівняння ) називається канонічним рівнянням еліпса

_{фокальні радіуси} =(R₁) _і =(R₂)

, .

Тоді рівність запишеться так:

.

З канонічного рівняння еліпса випливає ряд властивостей еліпса.

1º. Координатні осі є осями симетрії, а точка О перетин осей симетрії є центром симетрії еліпса. Це випливає із того, що біжучі координати і входять у парних степенях, тому якщо точка належить еліпсу, то точки , , теж належать еліпсу.

2º. Точками перетину еліпса з осями симетрії є точки , , , . Ці точки називаються вершинами еліпса.

Це випливає з того, що при , а при . Величини і називаються відповідно великою і малою осями еліпса, а і – півосями еліпса.

3º. Еліпс є обмеженою лінією. Це випливає із того, що 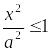і , звідки і , звідки маємо, що , .

4º. Якщо в рівнянні еліпса півосі збігаються, тобто , то дістанемо рівняння кола з центром в початку координат і радіусом .

Оскільки для еліпса , то при маємо, що . Таким чином, коло – це еліпс, в якого фокуси збігаються з центром еліпса.

Для характеристики еліпса вводять числову характеристику, якою є відношення півфокусної відстані до великої півосі, тобто , це число називається ексцентриситетом еліпса. Це число характеризує відхилення еліпса від кола, степінь „витягнутості” еліпса. Для кола , а для еліпса .