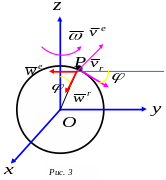
7. Теоремы о сложении скоростей и ускорений.

1.2. Теоремы о сложении скоростей и ускорений. Пусть некоторое пространство, рассматриваемое как твердое тело, движется относительно абсолютного пространства. Свяжем с подвижным пространством систему координат , а с неподвижной - . Рассмотрим движение точки . Точка меняет свое положение и относительно подвижной системы отсчета и относительно неподвижной. Условимся о следующей терминологии и обозначениях.

Абсолютное или сложное движение точки - движение относительно неподвижной системы координат.

Относительное движение точки - движение относительно подвижной системы координат.

Переносное движение точки - движение вместе с подвижным пространством.

Заметим, что если мысленно остановить переносное движение точки, то абсолютное движение будет совпадать с относительным движением и если остановить относительное, то абсолютное будет совпадать с переносным движением.

Определение 2. Скорость и ускорение точки в абсолютном, относительном и переносном движениях называются соответственно абсолютными и переносными скоростями и ускорениями точки и обозначать , .

Из приведенного определения вытекает, что

,

где - радиус-вектор точки в абсолютной системе отсчета, а в подвижной. Переносной скоростью и переносным ускорением точки будет скорость и ускорение той точки подвижного пространства, с которой в данный момент она совпадает. Пусть - векторы угловой скорости и углового ускорения подвижного пространства, а вектора скорости и ускорения начала подвижной системы отсчета. Тогда

.

Теорема 1 (О сложении скоростей). В любой момент времени имеет место равенство

.

Доказательство. За все время движения выполняется равенство

.

Продифференцируем это тождество по времени

.

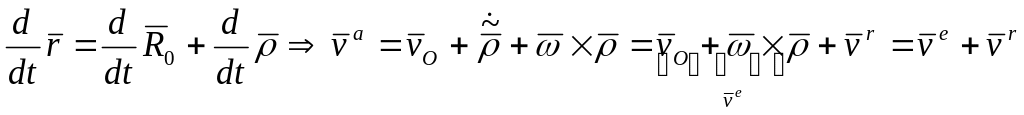Теорема доказана.

Теорема 2 (О сложении ускорений). В любой момент времени имеет место равенство

.

Доказательство. Из теоремы о сложении скоростей следует равенство

,

имеющее место в любой момент времени. Продифференцируем его по времени

.

Теорема доказана.

Определение 3. Вектор называется ускорением Кориолиса.

Теорему о сложении ускорений еще называют теоремой Кориолиса и записывают в виде равенства

.

Кориолисово ускорение обращается в ноль в следующих трех и только трех случаях

1) ; 2) ; 3) .

8. Кинематические уравнения Эйлера.

2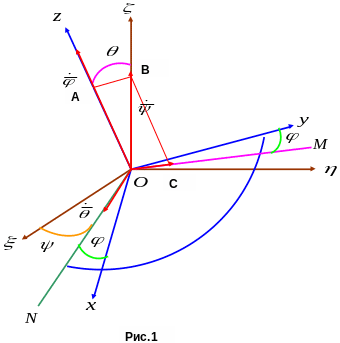 .4. Кинематические уравнения Эйлера. Пусть твердое тело совершает вращение относительно неподвижной точки , - абсолютная система координат - система координат, связанная с телом, - углы Эйлера.

Считая, что тело совершает одновременное вращение относительно пересекающихся в одной точке (точке ) осей , в силу предыдущего пункта запишем

, (1)

где вектор угловой скорости тела в абсолютном движении. Определим его проекции на оси подвижной системы отсчета как функции углов Эйлера и их производных.

Проведем линию перпендикулярную плоскости . В силу Эта линия лежит в плоскости , при этом , . Заметим, что по построению, , так как лежит в плоскости , , так как лежит в плоскости . Таким образом, лежат в одной плоскости (перпендикулярной ). Разложим вектор по направлениям и . Параллелограмм - прямоугольник. Тогда

.

Отсюда

Перепишем (1) с учетом последней формулы

. (2)

Спроектируем (2) на оси подвижной системы координат. Имеем

,

,

. (3)

Определение 1. Соотношения (3) называются кинематическими соотношениями Эйлера в подвижной системе отсчета.