
- •Подготовка к коллоквиуму №2 по теоретической механике вопросы с докозательством
- •1. Перемещение, скорость и ускорение произвольной точки твердого тела при повороте его относительно неподвижной оси.
- •2. Теорема Эйлера.
- •3. Перемещение, скорость и ускорение произвольной точки тела при его повороте относительно неподвижной точки.
- •4. Перемещение свободного твердого тела как сумма поступательного и вращательного. Теорема Шаля.
- •5. Винтовое перемещение свободного твердого тела.
- •6. Теоремы о существовании мгновенных центров скоростей и ускорений.
- •6.2. Мгновенный центр скоростей.
- •6.3. Мгновенный центр ускорений.
- •7. Теоремы о сложении скоростей и ускорений.
- •8. Кинематические уравнения Эйлера.
- •Сложение мгновенного поступательного и вращательного движений.
Подготовка к коллоквиуму №2 по теоретической механике вопросы с докозательством
1. Перемещение, скорость и ускорение произвольной точки твердого тела при повороте его относительно неподвижной оси.
3.2. Перемещение
произвольной точки твердого тела при
повороте его относительно неподвижной
оси. В процессе
поворота за время
![]() радиус, соединяющий точку с центром ее
траектории, повернется на один и тот же
угол
радиус, соединяющий точку с центром ее
траектории, повернется на один и тот же
угол
![]() для всех точек тела. Это обстоятельство
позволяет реализовать следующий способ
описания перемещения произвольной
точки тела. Введем абсолютную систему
отсчета
для всех точек тела. Это обстоятельство
позволяет реализовать следующий способ
описания перемещения произвольной
точки тела. Введем абсолютную систему
отсчета
![]() .
Начало отсчета
.
Начало отсчета
![]() поместим на ось вращения, ось
поместим на ось вращения, ось
![]() направим вдоль оси вращения, причем
так, чтобы вращение тела происходило
против часовой стрелки, если смотреть
на него с острия орта этой оси.
направим вдоль оси вращения, причем
так, чтобы вращение тела происходило
против часовой стрелки, если смотреть
на него с острия орта этой оси.
С
телом свяжем подвижную систему отсчета
![]() ,
которая в начальный момент
,
которая в начальный момент
![]() совпадала с неподвижной системой
.
Пусть
совпадала с неподвижной системой
.
Пусть
![]() - координаты произвольной точки тела в
подвижной системе отсчета. Очевидно,
что в процессе перемещения они не
меняются и
- координаты произвольной точки тела в
подвижной системе отсчета. Очевидно,
что в процессе перемещения они не
меняются и
![]() . (1)
. (1)
Координаты этой точки после перемещения в неподвижной системе имеют вид
![]()
 ,
,
![]()
![]() .
.
В силу (1) отсюда выводим
![]() ,
,
![]()
![]() .
.
Или в неподвижной системе
![]()
где
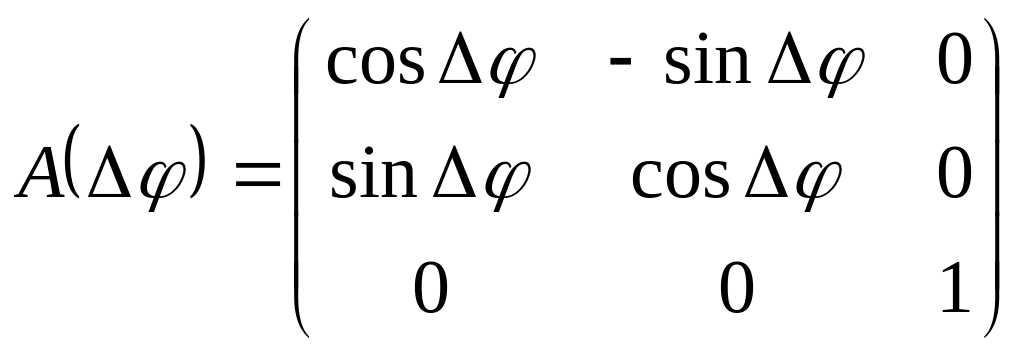 .
.
Непосредственно проверяется, что
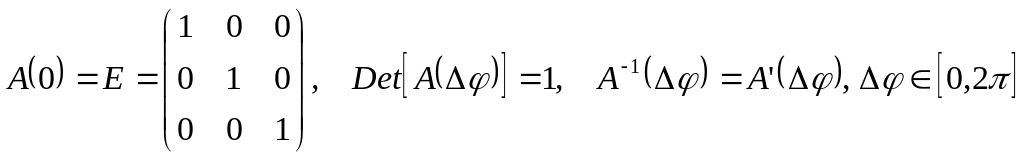 .
.
Таким образом, в проекциях на неподвижную систему для перемещения произвольной точки тела имеем
![]()
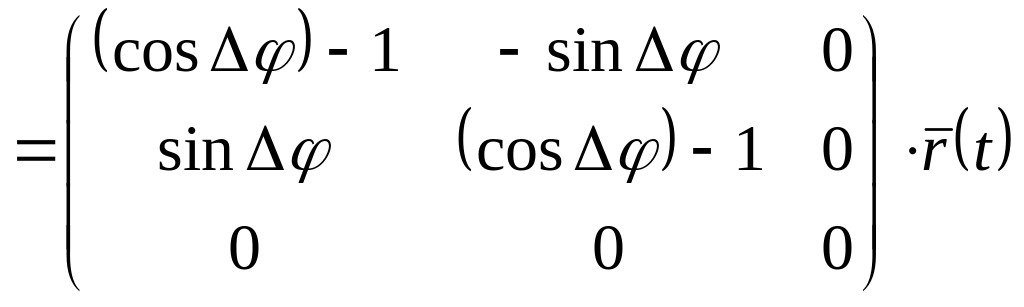 .
(2)
.
(2)
3.3. Скорость произвольной точки тела при вращении его относительно неподвижной оси. По определению скорости точки из (1.2) выводим
![]() .
(3)
.
(3)
С точностью до малых первого порядка справедливо
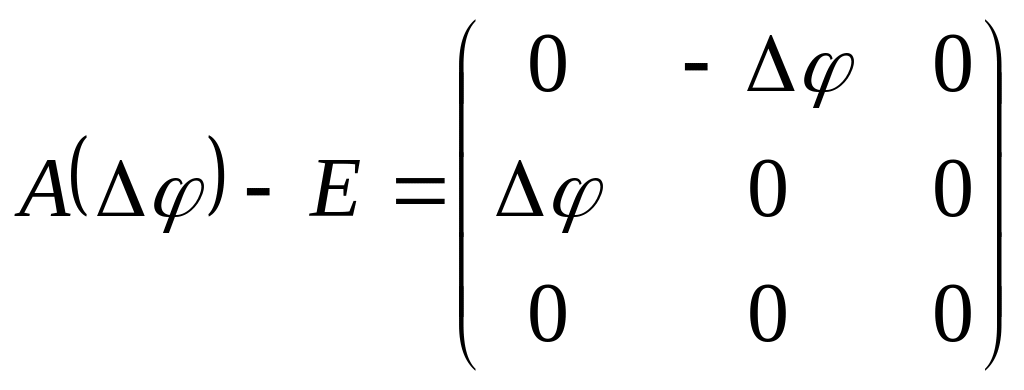 .
.
Подставим последнее выражение в (3). В результате получим
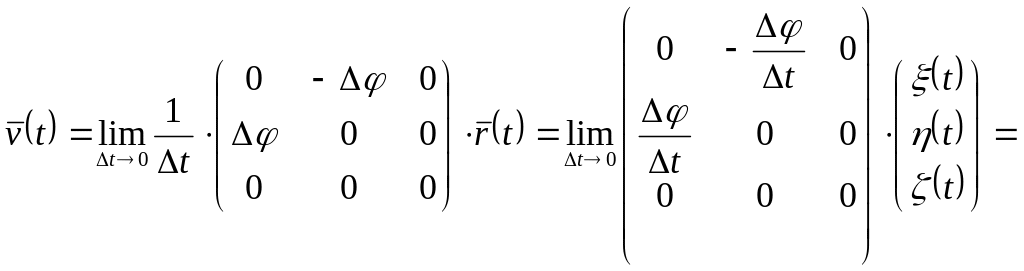
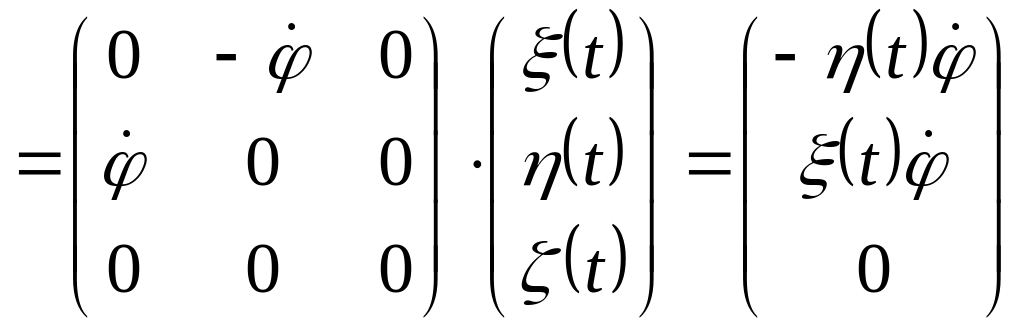 .
(4)
.
(4)
Непосредственно проверяется, что
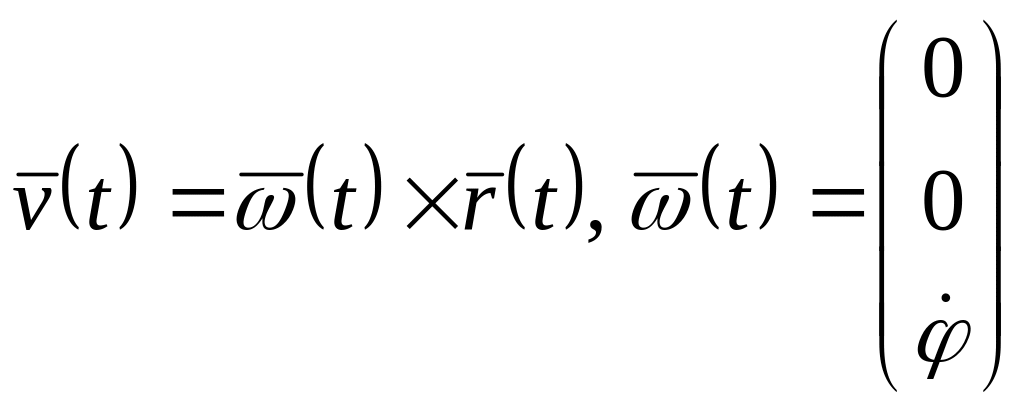 . (5)
. (5)
Формула (5) является базовой формулой для вычисления скорости произвольной точки тела, вращающегося относительно неподвижной оси.
Определение
1. Вектор
![]() называется угловой скоростью вращения
тела относительно неподвижной оси.
называется угловой скоростью вращения
тела относительно неподвижной оси.
Из
определения вектора угловой скорости
следует, что он направлен вдоль оси
вращения тела, при чем так, что вращение
тела видится с его конца происходящим
против часовой стрелки. По величине он
равен
![]() .
.
Из
формулы (5) следует, что
![]() ,
где
,
где
![]() - расстояние от точки до оси вращения,
а направлен вектор скорости, как это и
должно быть, по касательной к траектории.
- расстояние от точки до оси вращения,
а направлен вектор скорости, как это и
должно быть, по касательной к траектории.
3.4. Ускорение произвольной точки тела при вращении его относительно неподвижной оси. По определению ускорения точки находим
![]()
![]() .
(1)
.
(1)
Здесь
обозначено
![]() .
.
Определение
1. Вектор
![]() называется угловым ускорением вращения
тела относительно неподвижной оси.
называется угловым ускорением вращения
тела относительно неподвижной оси.
Нетрудно видеть, что
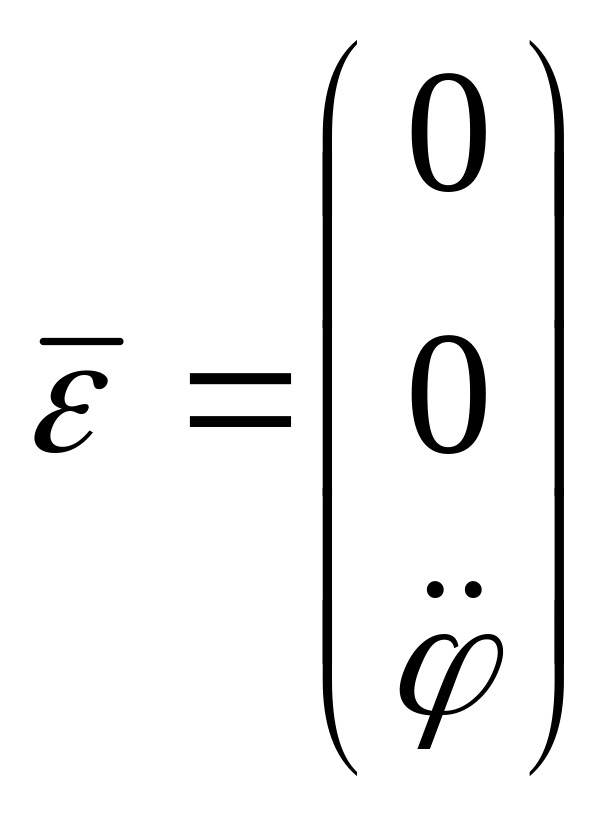 ,
,
поэтому вектор направлен вдоль неподвижной оси вращения.
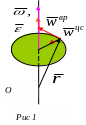 Из
формулы (1) следует, что вектор ускорения
точки можно представить в виде векторной
суммы двух слагаемых
Из
формулы (1) следует, что вектор ускорения
точки можно представить в виде векторной
суммы двух слагаемых
![]() .
.
Рассмотрим подробнее каждое из них.
Определение 2. Вектор
![]()
называется вращательным ускорением точки тела, вращающегося относительно неподвижной оси.
Вектор
вращательного ускорения направлен по
касательной к траектории точки, а по
величине равен
![]() ,
-
расстояние от точки до оси вращения.
,
-
расстояние от точки до оси вращения.
Преобразуем второе слагаемое в (1). По формуле
![]()
и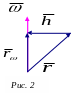 меем
меем
![]()
![]() .
.
Здесь
обозначено:
![]() - проекция вектора
- проекция вектора
![]() на неподвижную ось,
на неподвижную ось,
![]() - вектор направленный от точки к оси
вращения. Последнее обстоятельство
позволяет дать следующее определение.
- вектор направленный от точки к оси
вращения. Последнее обстоятельство
позволяет дать следующее определение.
Определение 3.
Вектор
![]()
называется осестремительным ускорением точки тела, вращающегося относительно неподвижной оси.
Из
определения видно, что осестремительное
ускорение всегда направлено в сторону
оси вращения, а по величине равно
![]() .
.
Для тела, вращающегося относительно неподвижной оси, траектории всех его точек будут окружности, плоскости которых перпендикулярны оси вращения тела, а центры лежат на этой оси, поэтому направление вращательного ускорения точки совпадает с касательной к траектории, а направление осестремительного ускорения – с нормалью к траектории точки. Таким образом, в данном случае вращательное ускорение является касательным ускорением, а осестремительное – нормальным ускорением точки.
Итак
![]() .
Отсюда, в силу
.
Отсюда, в силу
![]() выводим
выводим
![]() .
.
