14 Амплитудная волновая функция. Амплитудное уравнение Шредингера.

Потенциальная энергия, входящая в уравнение Шредингера, является в общем случае функцией координат и времени. Однако во многих практически важных задачах потенциальная энергия является функцией только координат и не зависит от времени. Для таких задач волновую функцию можно представить в виде:

, (18)

где Е – полная энергия микрочастицы.

Функция , зависящая только от координат, называется амплитудой волновой функции. Ее можно найти из уравнения

, (19)

которое называется амплитудным уравнением Шредингера.

Силовое поле, в котором потенциальная энергия микрочастицы не зависит от времени, называется стационарным. Состояния микрочастиц в стационарном поле называются стационарными состояниями. Т.е. амплитудное уравнение Шредингера описывает стационарные уравнения микрочастиц.

Каждое состояние микрочастицы описывается одной волновой функцией. Если уравнение Шредингера допускает решение в виде нескольких волновых функций, то это означает, что микрочастица может находиться в нескольких различных состояниях.

15 Главное квантовое число

Главное (радиальное) квантовое число — целое число, обозначающее номер энергетического уровня. Характеризует энергию электронов, занимающих данный энергетический уровень. Является первым в ряду квантовых чисел, который включает в себя главное, орбитальное и магнитное квантовые числа, а также спин. Эти четыре квантовых числа определяют уникальное состояние электрона в атоме (его волновую функцию). Главное квантовое число обозначается как  . При увеличении главного квантового числа возрастают радиус орбиты и энергия электрона.Главное квантовое число равно номеру периода элемента.

Наибольшее число электронов на энергетическом уровне с учётом спина электрона определяется по формуле 

16 Орбитальное квантовое число

Орбитальный момент количества движения L электрона может принимать лишь следующий ряд дискретных значений

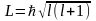, (24)

где - орбитальное квантовое число, которое может принимать любое значение из следующего ряда .

17 Магнитное квантовое число

Вектор орбитального момента количества движения может ориентироваться относительно вектора напряженности внешнего магнитного поля лишь так, что его проекция на направление вектора может быть только кратной величине , т.е.

. (25)

Число называется магнитным квантовым числом. Оно может принимать все целочисленные значения от до , включая 0:

всего значений.

Пусть , тогда , т.е. имеет три значения, тогда вектор орбитального момента количества движения ориентирован так, как показано на рис.5.

18 Спиновое квантовое число

Подобно массе и заряду, спин является первичным, неотъемленным свойством электрона (и других частиц), не имеющий аналогов в макромире.

На основании экспериментальных результатов доказано, что спин электрона по абсолютной величине равен:

, (26)

а его проекция на направление внешнегомагнитного поля (рис.6) может иметь лишь два значения

(27)

или , где называется спиновым квантовым числом, которое у электрона может принимать лишь два значения: 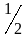и - .

Итак, с учетом наличия у электрона спина его состояние в водородо­подобном атоме задается четырьмя квантовыми числами: главным , орби­тальным , магнитным и спиновым . Энергия же электрона, зависит лишь от значения .

Интернет

Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д. Уленбек (1900—1974) и С. Гаудсмит (1902—1979) предположили, что электрон обладает собственным неуничто

Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.

Если электрону приписывается собственный механический момент импульса (спин) L_s, то ему соответствует собственный магнитный момент р_ms. Согласно общим выводам квантовой механики, спин квантуется по закону

где s — спиновое квантовое число.

По аналогии с орбитальным моментом импульса, проекция L_sz спина квантуется так, что вектор L_s может принимать 2s+1 ориентации. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s+1=2, откуда s= ½ жимым механическим моментом импульса, не связанным с движением электрона в пространстве, спином (см. §131).