12 Волновая функция.

Шредингер предположил, что существует некоторая функция координат пространства и времени 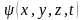, которая и является искомой характеристикой состояния микрочастицы. Он назвал ее волновой функцией и предложил уравнение для ее отыскания:

, (13)

где 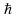- квант действия;

;

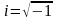m – масса покоя микрочастицы;

Ѳ - оператор Лапласа;

;

W(x,y,z,t) – потенциальная энергия микрочастицы во внешнем силовом поле; если микрочастица свободна, то W(x,y,z,t)=0.

Но оказывается, что физический смысл имеет произведение волновой функции y и комплексно сопряженной с ней функции :

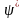y y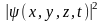^*= . (14)

Физический смысл произведения yy^* заключается в следующем:

Это произведение есть действительная функция, численное значение которой для данной точки пространства в данный момент времени, равно вероятности нахождения микрочастицы в единичном пространстве окружающем данную точку.

Эту вероятность обозначают W(x,y,z,t).

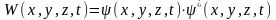(15)

или сокращенно

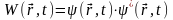. (16)

В соответствии с таким физическим смыслом волновая функция должна быть непрерывной и иметь непрерывную первую производную, однозначной и конечной во всех точках пространства, т.к. вероятность нахождения микрочастицы не может быть величиной неоднозначной, бесконечной или скачкообразно изменяться от точки к точке

13 Уравнение Шредингера, его особенности

Шредингер предположил, что существует некоторая функция координат пространства и времени , которая и является искомой характеристикой состояния микрочастицы. Он назвал ее волновой функцией и предложил уравнение для ее отыскания:

, (13)

где - квант действия;

;

m – масса покоя микрочастицы;

Ѳ - оператор Лапласа;

;

W(x,y,z,t) – потенциальная энергия микрочастицы во внешнем силовом поле; если микрочастица свободна, то W(x,y,z,t)=0.

Отметим особенности уравнения Шредингера:

1. Это уравнение – дифференциальное уравнение частных производных, хорошо известное как волновое уравнение; его решением являются функции, описывающие процесс распространения волн в пространстве.

2. Уравнению () могут удовлетворять только комплексные значения. Поскольку комплексные числа – это математическая абстракция, не имеющая физического смысла, то и волновая функция y тожже не имеет физического смысла и значит, сама по себе не характеризует состояние микрочастицы.

Но оказывается, что физический смысл имеет произведение волновой функции y и комплексно сопряженной с ней функции :

y y^*= . (14)

Физический смысл произведения yy^* заключается в следующем:

Это произведение есть действительная функция, численное значение которой для данной точки пространства в данный момент времени, равно вероятности нахождения микрочастицы в единичном пространстве окружающем данную точку.

Эту вероятность обозначают W(x,y,z,t).

(15)

или сокращенно

. (16)

В соответствии с таким физическим смыслом волновая функция должна быть непрерывной и иметь непрерывную первую производную, однозначной и конечной во всех точках пространства, т.к. вероятность нахождения микрочастицы не может быть величиной неоднозначной, бесконечной или скачкообразно изменяться от точки к точке

Отметим, что если мы рассматриваем поведение не одной, а совокупности (или системы) микрочастиц, то оно описывается их общей волновой функцией, зависящей от координат всех частиц. Например, для ситстемы из двух микрочастиц волновая функция имеет вид:

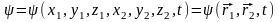, (17)

где x₁, y₁, z₁ – координаты первой микрочастицы;

x₂, y₂, z₂ - координаты второй микрочастицы.

Произведение имеет смысл вероятности того события, что в момент времени t одна из микрочастиц находится в единичном объеме, окружающем точку с координатами x₁, y₁, z₁ , а другая – в единичном объеме, окружающем точку с координатами x₂, y₂, z₂.

Потенциальная энергия, входящая в уравнение Шредингера, является в общем случае функцией координат и времени. Однако во многих практически важных задачах потенциальная энергия является функцией только координат и не зависит от времени. Для таких задач волновую функцию можно представить в виде:

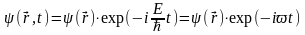, (18)

где Е – полная энергия микрочастицы.

Википедия:

Зависимое от времени уравнение

Наиболее общая форма уравнения Шрёдингера — это форма, включающая зависимость от времени^[1] :

Зависимое от времени уравнение (общий случай)

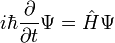
Пример нерелятивистского уравнения Шрёдингера для частицы движущейся в электрическом поле (без магнитного!):

Зависящее от времени уравнение Шрёдингера

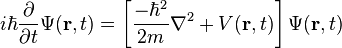
[править]Формулировка

[править]Общий случай

В квантовой физике вводится комплекснозначная функция  , описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.

Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения   в частных физических задачах. Таким уравнением является уравнение Шрёдингера.

Пусть волновая функция задана в n-мерном пространстве, тогда в каждой точке с координатами  , в определенный момент времени t она будет иметь вид  . В таком случае уравнение Шрёдингера запишется в виде:

где  ,   — постоянная Планка;   — масса частицы,   — внешняя по отношению к частицепотенциальная энергия в точке   в момент времени  ,   — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:

[править]Случай трёхмерного пространства

В трёхмерном случае пси-функция является функцией трёх координат и   в декартовой системе координат заменяется выражением

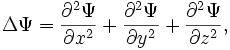
тогда уравнение Шрёдингера примет вид:

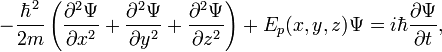
где  ,   — постоянная Планка;   — масса частицы,   — потенциальная энергия в точке  .

[править]Стационарное уравнение Шрёдингера

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда   не является функцией времени, можно записать в виде:

где функция   должна удовлетворять уравнению:

которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для   (2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).

Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции   от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции   совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции  .

Важное значение имеет интерпретация величины   в уравнении (2). Она производится следующим путём: временна́я зависимость функции   в уравнении (2) имеет экспоненциальный характер, причём коэффициент при   в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель  . В левой же части уравнения (3) функция   умножается на потенциальную энергию  . Следовательно, из соображений размерности вытекает, что величина   должна иметь размерностьэнергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что   представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера,   действительно является полной энергией частицы при движении, описываемом функцией  .