1. Пусть функция f(x), заданная в некотором промежутке* [a, b], во всех его точках является производной функции F(x) , также заданной в [a, b]. Тогда эта последняя функция F(x) называется первообразной функцией для функции f(x) (в промежутке [a, b]).

Имеет место

Теорема 1. У всякой непрерывной на промежутке [a, b] функции имеется первообразная.

Доказательство этой теоремы будет дано далее.

Нетрудно видеть, что, если функция F(x) есть первообразная для f(x), то функция F(x) + C при любом постоянном C также является первообразной для f(x). В то же время никаких других первообразных, кроме функций вида F(x) + C, у f(x) уже быть не может. Действительно, если F1(x) есть какая-то первообразная для f(x), то производная разности F1(x) - F(x) будет всюду на [a, b] равняться нулю, а тогда сама разность есть величина постоянная, т. е.

F1(x) - F(x) = C и F1(x) = F(x) + C.

Если F(x) есть первообразная функция для f(x), то функция двух аргументов x и C, равная F(x) + C, называется неопределенным интегралом функции f(x) и обозначается символом

Таким образом, неопределенный интеграл какой-нибудь функции представляет собой общий вид первообразных функций для этой функции. Величина C, входящая в определение неопределенного интеграла, называется "произвольной постоянной". Придавая ей то или иное закрепленное значение, можем получить из неопределенного интеграла любую первообразную.

Легко понять, что из самого определения понятия интеграла вытекает следующее утверждение:

Теорема 2. Производная неопределенного интеграла равна подинтегральной функции, т. е.

2. Подведение функции под знак дифференциала

На уроке Неопределенный интеграл. Примеры решений мы научились раскрывать дифференциал, напоминаю пример, который я приводил: То есть, раскрыть дифференциал – это почти то же самое, что найти производную.

3. формула интегрирования

4. Интегрирование простейших рациональных дробей.

Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:

У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:

где

Затем применяются следующие формулы:

Интеграл может быть вычислен за k шагов с помощью формулы редукции

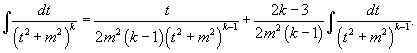
5.

6. Интегрирование тригонометрических функций

1°. Интегралы вида

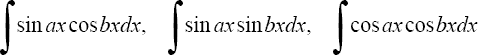
находятся с помощью тригонометрических формул

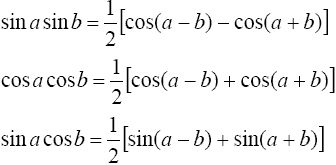
2°. Интегралы вида

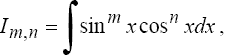
где m и n - четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

7.

8. Пусть функция f (x) ограничена на отрезке [a, b] и τ – разбиение этого отрезка точками

a = x 0 < x 1 < … < x i - 1 < x i < … < x n = b.

Обозначим через m i и M i соответственно точную нижнюю и точную верхнюю грани этой функции на отрезке [ x i - 1, x i] и составим следующие суммы:

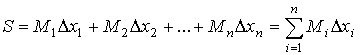
Эти суммы называются соответственно верхней и нижней суммами Дарбу функции f (x)для данного τ – разбиения отрезка [a, b]. Из определения нижней и верхней граней следует, что

mi ≤ f ( ξi ) ≤ Mi при

вследствие чего имеем

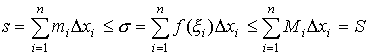
т. е. любая интегральная сумма и суммы Дарбу для данного разбиения связаны неравенствами s ≤ σ ≤ S. Суммы Дарбу имеют простой геометрический смысл. Рассмотрим неотрицательную непрерывную функцию f (x) на [a, b] и криволинейную трапецию, т. е. фигуру, ограниченную графиком функции f (x), двумя вертикальными прямыми, проведенными через точки a и b оси Ох, и осью Ох. Поскольку функция f (x) непрерывна на [a, b], она непрерывна и на [x i - 1, x i]. По второй теореме Вейерштрасса функция f(x) достигает на [x i - 1, x i] свои точные грани, и, следовательно, m i и M i — соответственно наименьшее и наибольшее значения функции на этом отрезке. Поэтому сумма S равна площади заштрихованной на ступенчатой фигуры, «описанной» около криволинейной трапеции, а сумма s равна площади ступенчатой фигуры, «вписанной» в данную криволинейную трапецию. (Смотри рисунок)

Следует особо отметить, что суммы Дарбу зависят только от разбиения отрезка [a, b], в то время как интегральная сумма σ зависит еще и от выбора точек ξ i на частичных отрезках [ x i - 1, xi ]. При фиксированном разбиении отрезка [a, b] суммы s и S – некоторые числа, а сумма σ – переменная величина, так как точки ξ i произвольны.

9.

10.

Теорема 1. Для того, чтобы ограниченная на отрезке [a,b] функция f(x) была интегрируемой на этом отрезке, необходимо и достаточно, чтобы для любого ε>0 нашлось такое разбиение Т сегмента [a,b], для которого

S-s≤ε (3)

Доказательство. Необходимость:

Пусть функция f(x) интегрируема на отрезке [a,b]. Обозначим через I предел интегральных сумм этой функции. По определению предела интегральных сумм для любого ε>0 существует δ>0 такое, что для любого разбиения Т, удовлетворяющего условию ∆<δ, независимо от выбора точек ζi на частичных сегментах выполняется неравенство

|I{xi, ζi} – I|<ε\4 (4)

Зафиксируем любое разбиение T. Для него согласно свойству верхних и нижних сумм для данного разбиения Т можно указать такие две интегральные суммы ζi’и ζi’’, что

S-I{xi, ζi’}≤ε\4, I{xi, ζi’’}-s≤ε\4 (5)

Отметим, что обе интегральные суммы I{xi, ζi’} и {xi, ζi’’} удовлетворяют неравенству (4). Из соотношения S –s = (S – I{xi, ζi’}) + (I{xi, ζi’}–I) +(I - {xi, ζi’’}) +({xi, ζi’’} – s) и неравенств (4) и (5) следует, что S – s < ε,

11.

Теорема. Непрерывная на сегменте [a, b] функция f(x) интегрируема на этом сегменте.

Доказательство. Пусть дано любое ε > 0. В силу равномерной непрерывности функции f(x) на сегменте [a, b] для положительного числа ε/(b - a) можно указать такое δ > 0, что при разбиении T сегмента [a, b] на частичные сегменты [xi-1, xi], длины Δxi которых меньше δ, колебание ωi функции f(x) на каждом таком частичном сегменте будут меньше ε/(b - a) , Поэтому для таких разбиений T

Следовательно, для непрерывной на сегменте [a, b] функции f(x) выполнены достаточные условия интегрируемости.

12. Интегрируемость некоторых разрывных функций.

Интегрируемость некоторых разрывных функций

Будем говорить, что точка x покрыта интервалом, если эта точка принадлежит указанному интервалу. Докажем следующую теорему.

Теорема. Если функция f(x) определена и ограничена на сегменте [a, b] и если для любого положительного числа ε можно указать конечное число интервалов, покрывающих все точки разрыва этой функции и имеющих общую сумму длин меньше ε, то f(x) интегрируема на сегменте [a, b].

Доказательство. Пусть дано любое ε > 0. Покроем точки разрыва функции f(x) конечным числом интервалов, сумма длин которых меньше , где M и m - точные верхняя и нижняя грани f(x) на сегменте [a, b] (случай M = m можно исключить, так как тогда f(x) ≡ c ≡ const). Точки сегмента, не принадлежащие указанным интервалам, образуют множество, состоящее из конечного числа непересекающихся сегментов. На каждом из них функция f(x) непрерывна и поэтому равномерно непрерывна. Разобъем каждый такой сегмент так, чтобы колебание ωi функции f(x) на любом частичном сегменте разбиения было меньше . Объединяя эти разбиения и интервалы, покрывающие точки разрыва функции f(x), получим разбиение T всего сегмента [a, b]. Для этого разбиения слагаемые суммы (равной S - s) разделяются на две группы и , причем в первую группу входят все слагаемые, отвечающие частям разбиения T, образованным из интервалов, покрывающих точки разрыва, а во вторую - остальные слагаемые. Так как колебания ωi = Mi - mi для слагаемых первой группы удовлетворяют неравенству ωi ≤ M - m, то

Для слагаемых второй группы . Поэтому

Таким образом,

Итак, для указанной в условии теоремы функции f(x) выполнены достаточные условия интегрируемости. Теорема доказана.

13. Интегрируемость монотонных ограниченных функций.

Интегрируемость монотонных ограниченных функций

Теорема. Монотонная на сегменте [a, b] функция f(x) интегрируема на этом сегменте**.

Доказательство. Ради определенности докажем теорему для неубывающей на сегменте [a, b] функции f(x). Зададимся произвольным положительным числом ε и разобъем сегмент [a, b] на равные части, длины которых меньше (случай f(a) = f(b) можно исключить, так как тогда f(x) ≡ const). Оценим для этого разбиения разность .

Имеем

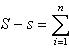
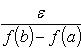
Но для неубывающей функции , поэтому S - s < ε. Теорема доказана.

14. Основные свойства определенного интеграла

Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.

Теорема 1. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], то

т. е. интеграл суммы равен сумме интегралов слагаемых.

Теорема 2. Если f(x) - непрерывная функция, а c - постоянное число, то

т. е. постоянный множитель можно выносить за знак интеграла.

Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.

В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = xm, то