Работа 3. Адсорбция поверхностно-активных веществ из водных растворов

Цель работы: определение основных характеристик поверхностного слоя на границе раствор — воздух и определение геометрических характеристик адсорбционного слоя.

Зависимость между изменением свободной поверхностной энергии на поверхности раствора и концентрацией вещества в поверхностном слое, т. е адсорбцией на границе раздела фаз, выражена уравнением Гиббса:

где Г — избыток вещества в моль на 1 см² поверхности раздела;

а — активность растворенного вещества в растворе;

R— газовая постоянная, равная 8,31 • 107. эрг/моль-град (8,31 • 10³ дж/кмоль-град)

Т — абсолютная температура.

Для разбавленных растворов можно принять, что вели­чина a равна концентрации C, а следовательно:

(3.1)

Это фундаментальное уравнение, являясь приложением вто­рого начала термодинамики к поверхностям раздела фаз, дает количественное выражение для распределения растворенного вещества между объемом и поверхностным слоем в результате самопроизвольных процессов, приводящих к уменьшению сво­бодной поверхностной энергии.

По величине поверхностной активности вещества делятся на:

1) поверхностно-активные вещества (ПАВ), которые понижают поверхност­ное натяжение ( < 0), их адсорбция (Г) положительна;

2) поверхностно-инактивные, которые повышают , оно возрастает при повышении концентрации, их адсорбция отрицательна ( > 0).

Величина производной, взятая с отрицательным знаком, называется поверх­ностной активностью и обозначается буквой g

Поверхностная активность является мерой способности рас­творенного вещества понижать поверхностное натяжение и пе­реходить из объема в поверхностный слой, т. е. адсорбиро­ваться. Из уравнения Гиббса видно, что адсорбция Г прямо пропорциональна поверхностной активности g при данной тем­пературе и концентрации веществ в растворе.

Уравнение Гиббса позволяет построить кривую зависимости Г от с на основании измерений поверхностного натяжения рас­творов различной концентрации. Для этого по данным опыта строят кривую  – С и находят для отдельных значений С произ­водные, проводя касательные и измеряя тангенсы углов накло­на. По этим данным вычисляют значения Г. Следует отметить, что крутизна наклона характеризует поверхностную активность.

Другой путь, более распространенный, хотя и менее точный, состоит в вычислении конечных разностей величин поверхност­ного натяжения ₁ и ₂, измеренных при двух различных концен­трациях С₁ и С₂. Эти разности ₂ - ₁=∆ и С₂ – С_l = ∆С под­ставляют в уравнение Гиббса:

(3.2)

(в качестве С в этом случае подставляют среднее арифметическое ).

Определение разностей и ход зависимости вычисленных зна­чений Г от С показывает рис. 3.1.

Уравнение Гиббса Г = f(,C) не дает однозначного выраже­ния для функции Г = f(с), т. е. для изотермы адсорбции, так как термодинамическое описание системы, включающей поверх­ность раздела, содержит не менее 3 переменных (в данном слу­чае , С, Г) по условию равновесия, выражаемому уравнением Гиббса. Для исключения одной из независимых переменных (на­пример, ) необходимо наложить дополнительное условие, кото­рое может быть получено при помощи молекулярной теории. Таким условием является, например, то или иное представление о строении поверхностного слоя. В первом приближении можно считать, что на границе раствор — воздух и во многих случаях, на границе, раствор — твердое тело поверхностный слой яв­ляется мономолекулярным, так как поле молекулярных сил твердого тела в основном экранируется первым слоем молекул. Молекулы ПАВ имеют резко выраженное асимметрическое строение и содержат как полярные (гидрофильные), так и непо­лярные (гидрофобные) группы. Вследствие такой асимметрично­сти строения молекулы, находясь в поверхностном слое, ориенти­руются таким образом, что их гидрофильная группа обращена к воде, а гидрофобная - к воздуху или вообще к менее полярной сре­де: гидрофильные группы – NH₂, ОН, SH, СООH и др.; гид­рофобные - углеводородные цепи или циклы. По мере того, как молекулы ПАВ все более и более тесно располагаются на поверхности, уменьшается поверхностное натя­жение на этой поверхности. С дальнейшим ростом концентра­ции молекулы принимают вер­тикальную ориентацию, зани­мая минимальную площадь в поверхностном слое, приобре­тающем свойства двухмерной ориентированной структуры анизотропной жидкости или твердого тела.

Дальнейшее увеличение чис­ла молекул в поверхностном слое невозможно, следователь­но, с ростом концентрации ве­щества в растворе наступает предел адсорбции. Предельное число молей вещества, а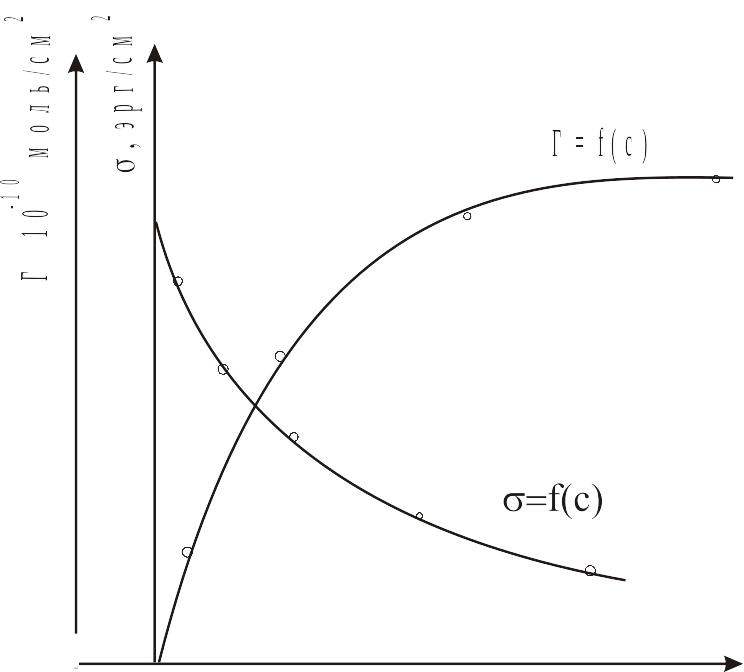 дсорбированных на 1 см² поверхности раздела, обозначают Г_. Исходя из представления о мономолекулярности слоя, Ленгмюр вывел следующее выражение для изотермы адсорбции:

(3.3)

В этом уравнении величины Г и Г_ обозначают не избыточ­ное, а полное количество ПАВ в 1 см² поверхностного слоя. Однако для разбавленных растворов этим различием можно пренебречь. Уравнение содержит две константы Г_ и k. Константа k является константой равнове­сия; в рамках молекулярно-кинетической теории она предста­вляет собой отношение констант скоростей процессов адсорбции и десорбции, термодинамически она характеризует работу ад­сорбции, равную RT Ink. Константа зависит от природы раство­ренного вещества и характеризует его поверхностную активность.

Уравнение Лэнгмюра хорошо согласуется с данными опыта и правильно отражает ход кривой Г=f(с), а именно: при ма­лых концентрациях (kC<<1) уравнение дает прямую пропор­циональность между адсорбцией Г и концентрацией C; при больших концентрациях (kC>>1) уравнение приводит к пре­дельному значению адсорбции Г = Г_. Уравнение (3.3) позво­ляет вычислить константы, в частности величину Г_ являю­щуюся важнейшей характеристикой, позволяющей вы­числить размеры адсорбируемых молекул.

Для нахождения кон­стант следует решить систему уравнений с двумя неизвестными, написанную для двух растворов различной концентрации (С₁ и С₂):

;

Разделив одно уравнение на другое, получим:

Решая подобные системы для различных пар (например, для пяти растворов различной концентрации можно составить 10 различных пар), находят зна­чения k, берут среднее и, подставляя его во все исходные уравнения, получают значения Г_, из которых вычисляют среднее арифметическое.

Другой способ вычисления констант предполагает использование графического метода. Для этого преобразуют урав­нение (3.3) так, чтобы получить уравнение прямой, например, де­лят С на обе части уравнения. После сокращения получают

т.е. уравнение типа y=a+bx.

В координатах (С/Г, С) уравнение отвечает прямой, не проходящей через начало координат. Величину, Г_ определяют по углу наклона прямой, а именно:

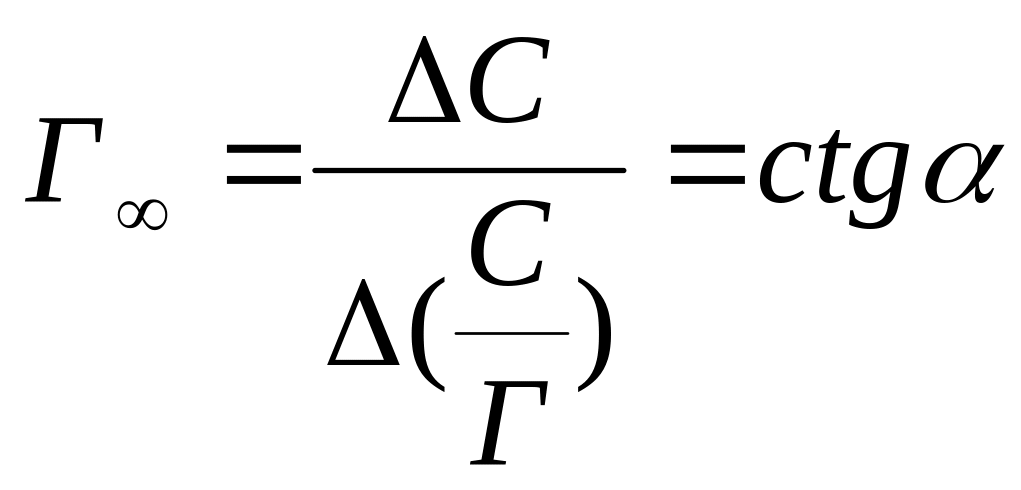
Построив график , находят разности величин ∆С и ∆(С/Г),

отвечающие отрезкам на графике (рис. 3.2), и вычис­ляют Г_. По отрезку отсекаемому на оси ординат, можно, определив Г_, найти вторую константу k.

П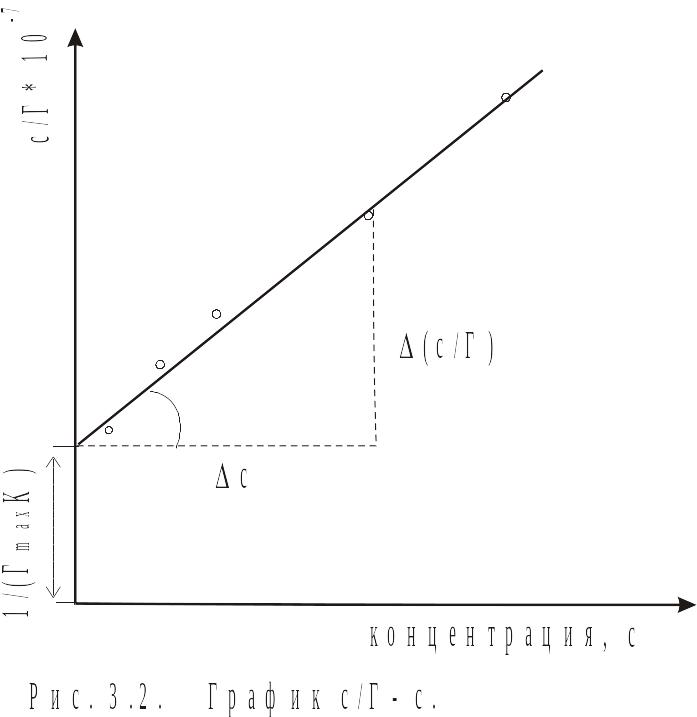 ользуясь изложенными представлениями о плотнейшей упа­ковке молекул в монослое при предельной адсорбции, можно вычислить площадь, занимаемую одной молекулой, т.е. попереч­ное сечение молекулы. Для этого надо разделить величину пло­щади на число молекул; на площади 1 см², согласно определе­нию величины Г, адсорбируются Г молей или ГN молекул (где N — число Авогадро). Следовательно, площадь занимаемая одной молекулой:

Можно также вычислить толщину поверхностного слоя , иначе говоря, осевую длину ориентированной молекулы. Массу вещества, адсорбированного на 1 см², с одной стороны, можно оп­ределить, как число молей Г_, умно­женное на молекулярный вес:

d = Г_M

где d – плотность вещества ПАВ

Таким образом:

Практическая часть

Задание 1. Вычисление изотермы адсорбции

По полученным в предыдущей работе (определение поверхностного натяжения растворов ПАВ методом сталагмометра) данным вычисляют значения Г, располагая данные и вычисления по следующей форме:

Таблица 3.1

Результаты измерений поверхностного натяжения и вычисления изотермы адсорбции

С		∆С	∆	∆/∆С	Сср	Г*10-10	Сср/Г*10-7

Результаты вычислений наносят на кривую Г– С_ср и вычисляют величину предельной адсорбции Г_ графическим методом из кривой С/Г–С_ср или расчетным методом. Вычисляют площадь, занимаемую молекулой в поверхностном слое и толщину слоя .

СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА ПО РАБОТЕ

Отчет по работе содержит название, цели, краткое описание работы и выводы о структуре адсорбционного слоя. Экспериментальные данные оформляются графически и заносятся в табл. 3.1.

Контрольные вопросы по работе 3.

1. Укажите природу констант в уравнении Ленгмюра и методы их определения.

2. Дайте определение предельной адсорбции в теории мономолекулярной адсорбции. В чем заключаются графические методы определения величины предельной адсорбции.