14. Условный экстремум

Пусть   — открытое множество и на   заданы функции  . Пусть  .

Эти   уравнения называют уравнениями связей (терминология заимствованна из механики).

Пусть на G определена функция  . Точка   называется точкой условного экстремума функции   относительно уравнений связи, если она является точкой обычного экстремума   на множестве E (рассматриваются окрестности  ).

Метод множителей Лагранжа для решения задачи условного экстремума

]Теорема

Пусть   — точка условного экстремума функции   при выполнении уравнений связи. Тогда в этой точке   градиенты   являются линейно зависимыми, то есть   но  .

Следствие

Если   — точка условного экстремума функции   относительно уравнений связи, то   такие, что в точке   или в координатном виде  .

]Достаточное условие условного экстремума

Пусть   является стационарной точкой функции Лагранжа   при  . Если   — отрицательно (положительно) определена квадратическая форма переменных   при условии  , то   является точкой max (min для положительно определенной) условного экстремума. Если она при этих условиях не является знакоопределенной, тогда экстремума нет.

15. Сущность мнк

Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x

где   — вектор неизвестных параметров модели

 — случайная ошибка модели.

Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть   — номер наблюдения ( ). Тогда   — значения переменных в  -м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:

Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):

Величина остатков зависит от значений параметров b.

Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков будет минимальной:

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях возможно аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции ESS(b) — продифференцировать функцию   по неизвестным параметрам b, приравнять производные к нулю и решить полученную систему уравнений:

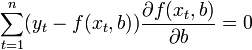
Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).

Обобщенный МНК

Основная статья: Обобщенный метод наименьших квадратов

Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определенную квадратичную форму от вектора остатков  , где   — некоторая симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно из теории симметрических матриц (или операторов) для таких матриц существует разложение  . Следовательно, указанный функционал можно представить следующим образом  , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).

Доказано (теорема Айткена), что для обобщенной линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещенных оценок) являются оценки т. н. обобщенного МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок:  .

Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид

Ковариационная матрица этих оценок соответственно будет равна

Фактически сущность ОМНК заключается в определенном (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.

]Взвешенный МНК

В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК (WLS — Weighted Least Squares). В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: 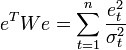 . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.