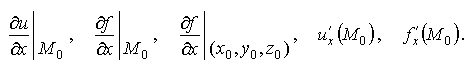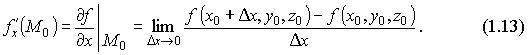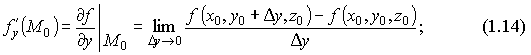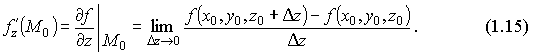1.Понятие функции двух и более переменных Многие явления, происходящие в природе, экономике, общественной жизни нельзя описать с помощью функции одной переменной. Например, рентабельность предприятия зависит от прибыли, основных и оборотных фондов. Для изучения такого рода зависимостей и вводится понятие функции нескольких переменных. В данной лекции рассматриваются функции двух переменных, так как все основные понятия и теоремы, сформулированные для функций двух переменных, легко обобщаются на случай большего числа переменных. Пусть   – множество упорядоченных пар действительных чисел  . Определение 1. Если каждой упорядоченной паре чисел   по некоторому закону   поставлено в соответствие единственное действительное число  , то говорят, что задана функция двух переменных   или  . Числа   называются при этом независимыми переменными или аргументами функции, а число   – зависимой переменной. Например, формула  , выражающая объем цилиндра, является функцией двух переменных:   – радиуса основания и   – высоты. Пару чисел   иногда называют точкой  , а функцию двух переменных – функцией точки  . Значение функции   в точке   обозначают   или   и называют частным значением функции двух переменных. Совокупность всех точек  , в которых определена функция  , называется областью определения этой функции. Для функции двух переменных область определения представляет собой всю координатную плоскость или ее часть, ограниченную одной или несколькими линиями. Например, область определения функции   – вся плоскость, а функции   – единичный круг с центром в начале координат (  или  .

2.Функции двух переменных       Приращение функции 

     Функция, дифференцируемая в точке   

 при 

В этом случае дифференциал функции в точке  :

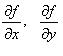 - частные производные, вычисленные в точке  .

     Дифференцирование композиции 

     1. Если   то

2. Если то:

     Однородная функция степени k 

3. Пределы и непрерывность

Исследование пределов и непрерывности в многомерных пространствах приводит ко многим нелогичным и патологическим результатам, не свойственным функциям одной переменной. Например, существуют скалярные функции двух переменных, имеющих точки в области определения, которые при приближении вдоль произвольной прямой дают специфический предел, и дают другой предел при приближении вдоль параболы. Функция

стремится к нулю по любой прямой, проходящей через начало координат. Однако, когда к началу координат приближаются вдоль параболы  , предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует.

Функция   имеет пределом число A при стремлении переменных  , соответственно, к  , если для каждого число   найдется такое число  , что  , то есть  .

Функция   называется непрерывной в точке  , если предельное значение этой функции в точке   существует и равно частному значению  .

Функция   называется непрерывной на множестве  , если она непрерывна в каждой точке этого множества.

4. Частное и полное приращение функции.

Полное приращение функции 

z=f(x+x, y+y)f(x,y)

Частное приращение функции 

x z=f(x+x)f(x,y)

y z=f(x,y+y)f(x,y)

Вообще, полное приращение функции не равно сумме частных приращений.

Пример. z=xy. 

x z=(x+x)yxy=yx

y z=x(y+y)xy=xy

z=(x+x)(y+y)xy=yx+xy+yx  y z+x z.

5.

Частные производные первого порядка

Будем рассматривать функции трех независимых переменных. Пусть в некоторой трехмерной области Vзадана функция u=f(x,y,z) переменных x,y,z и пусть M0(x0,y0,z0) - некоторая внутренняя точка V. Дадим независимому переменному x приращение Δx=x-x0, тогда функция и получит так называемое частное приращение по x: Определение 1.7 Если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M0(x0,y0,z0) к вызвавшему его приращению Δx при Δx   0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М0 и обозначается одним из символов: По определению, Частные производные по y и по z определяются аналогично: Производные f'x, f'y, f'z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными. Так как частное приращение Δxf(M0) получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'x(M0) может рассматриваться как производная функции f(x,y0,z0) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x. Аналогично вычисляются частные производные по другим независимым переменным. Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция.

Рассмотрим функцию z=f(х,у) двух независимых переменных и установим геометрический смысл частных переменных z'_x=f'_x(х,у) и z'_y=f'_y(х,у).

В этом случае уравнение z=f(х,у) есть уравнение некоторой поверхности (рис.1.3). Проведем плоскость y = const. В сечении этой плоскостью поверхности z=f(х,у) получится некоторая линия l₁ пересечения, вдоль которой изменяются лишь величины х и z.

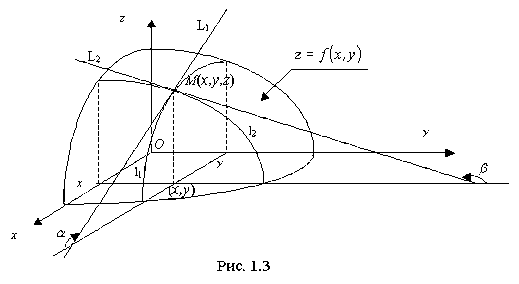
Частная производная z'_x (её геометрический смысл непосредственно следует из известного нам геометрического смысла производной функции одной переменной) численно равна тангенсу угла α наклона, по отношению к оси Ох , касательной L₁ к кривой l₁, получающейся в сечении поверхности z=f(х,у) плоскостью y = const в точке М(х,у,f(xy)): z'_x= tgα.

В сечении же поверхности z=f(х,у) плоскостью х = const получится линия пересечения l₂, вдоль которой изменяются лишь величины у и z. Тогда частная производная z'_y численно равна тангенсу угла β наклона по отношению к оси Оу, касательной L₂ к указанной линии l₂пересечения в точке М(х,у,f(xy)): z'_x= tgβ.

6. Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.

Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:

где функции   и   определены и непрерывны в некоторой области  .

Выясним каков геометрический смысл дифференциала. Возьмем на графике функции y = f(x) произвольную точку M(x,y) (рис21.). Проведем касательную к кривой y = f(x) в точке M, которая образует угол  с положительным направлением оси OX, то есть f'(x) = tg . Из прямоугольного треугольника MKN

KN = MNtg xtg  = f'(x) x,

то есть dy = KN.

Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение  x.

7. Рассмотрим для примера функцию

от двух переменных, которую будем предполагать дифференцируемой.

Мы хотим вычислить эту функцию в точке  , где

,

,

Приближенные значения этих чисел запишем в виде конечных десятичных дробей

,

.

Таким образом, имеют место приближенные равенства

с абсолютными погрешностями приближения, удовлетворяющими неравенствам

.

Подставив в функцию   вместо   соответственно  , получим приближенное равенство

с абсолютной погрешностью

,

которую при достаточно малых   можно приближенно заменить дифференциалом функции   в точке  :

.

Отсюда получаем неравенство

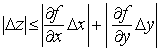.                               (1)

На самом деле это неравенство приближенное, потому что мы получили его, пренебрегая некоторой величиной, правда, значительно меньшей, чем  .

Обратим внимание на тот факт, что конечные десятичные дроби   при уменьшении  ,   становятся все более и более громоздкими. Поэтому при вычислении числа   мы должны беспокоиться не только о том, чтобы оно приближало   должным образом, но и чтобы производимые при этом вычисления совершались возможно, экономно. В силу этого замечания из неравенства (1) следует, что если нужно, чтобы абсолютная погрешность   не превышала данную малую величину, которую мы обозначим через  , то этого мы достигнем, взяв числа   ,   такими, чтобы выполнялись неравенства

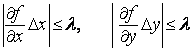 ,                       (2)

т. е. чтобы погрешность   распределялась между слагаемыми в правой части неравенства (1) поровну.

Из неравенств (2) видно, что вычисления будут наиболее экономными, если в качестве  ,   (на самом деле  ,  ) взять наибольшие возможные числа, удовлетворяющие этим неравенствам.