16. Розкладання вектора по базису.

Пара точок називається впорядкованою, якщо про них відомо, яка з точок є першою, а яка - другий. Відрізок з впорядкованими кінцями називається спрямованим відрізком або вектором. Базисом в векторному просторі називається така упорядкована лінійно незалежна система векторів, що будь-який вектор простору розкладається по ній. Коефіцієнти при даному розкладі є координатами вектора в цьому базисі.

17. Декартова система координат. Ортоганальний базис.

Декартовою системою координат називається сукупність однієї, двох, трьох або більше пересічних координатних осей, точки, в якій ці осі перетинаються - початок координат - і одиничних відрізків на кожній з осей. Кожна точка в системі координат визначається впорядкованим набором кількох чисел - координат. У конкретній координатній системі кожній точці відповідає один і тільки один набір координат. Ортогональний базис — базис, складений з попарно ортогональних векторів. Приклад декартової системи координат:

двовимірна тривимірна

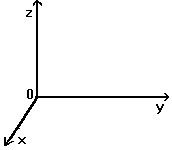
19. Поділ відрізка в даному відношенні.

1. Поділ відрізка в даному відношенні.

Нехай точки А, В мають координати , .

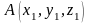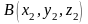Якщо відрізок АВ поділимо точкою М у відношенні: 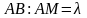, то координати точки М знаходять за формулами:

; .

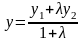
Якщо , то отримуємо формули для знаходження координат середини відрізка.

Задача

Відрізок з кінцями і 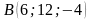, ділиться в точці М навпіл. Знайдіть довжину відрізка МК, де .

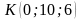Розв’язання. Знайдемо координати точки М за формулами:

; ; ;

.

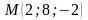Тоді координати вектора , .

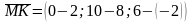Довжина вектора .

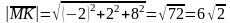20. Скалярний добуток векторів, його властивості. Приклад.

Скалярним добутком векторів а на b називається число, яке обчислюється по формулі:

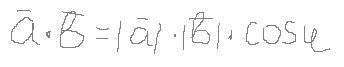
Властивості:

1. a*b=b*a

2. k*(a*b)=(k*a)*b=a*(k*b)

3. (a+b)c=a*c+b*c

4. a b=>a*b=0

Приклад:

21.Определение скалярного произведения векторов.

Определение.

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Скалярное произведение векторов и будем обозначать как . Тогда формула для вычисления скалярного произведения имеет вид 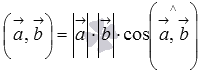, где и - длины векторов и соответственно, а 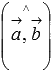- угол между векторами и .

Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .

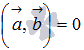Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению .

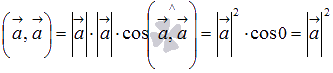Определение.

Скалярное произведение вектора на себя называется скалярным квадратом.

Формулу для вычисления скалярного произведения можно записать в ви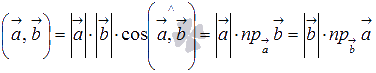де , где - числовая проекция вектора на направление вектора , а - числовая проекция вектора на направление вектора .

Таким образом, можно дать еще одно определение скалярного произведения двух векторов.

Определение.

Скалярным произведением двух векторов и называется произведение длины вектора на числовую проекцию вектора на направление вектора или произведение длины вектора на числовую проекцию вектора на направление вектора .

Это определение эквивалентно первому.

К началу страницы

Скалярное произведение в координатах.

Покажем как скалярное произведение вычисляется через координаты векторов в прямоугольной системе координат на плоскости и в пространстве.

Определение.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов и .

То есть, для векторов на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид 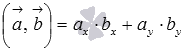, а для векторов в трехмерном пространстве скалярное произведение в координатах находится как .

Таким образом, мы имеем третье определение скалярного произведения. Покажем, что это определение эквивалентно первому.

Сначала докажем равенства 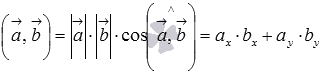для векторов на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы и . Тогда (при необходимости обращайтесь к статьям операции над векторами и их свойства и операции над векторами в координатах).

Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов мы можем записать . Так как 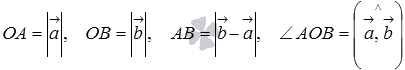, то последнее равенство можно переписать как 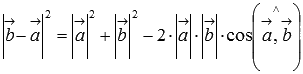, а по первому определению скалярного произведения имеем , откуда .

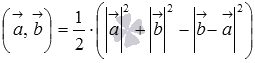Вспомнив формулу вычисления длины вектора по координатам, получаем

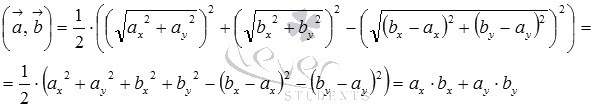
Абсолютно аналогично доказывается справедливость равенств для векторов , заданных в прямоугольной системе координат трехмерного пространства.

Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости 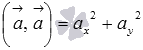, в пространстве .

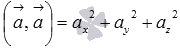К началу страницы

Свойства скалярного произведения.

Для любых векторов и справедливы следующие свойства скалярного произведения:

1. свойство коммутативности скалярного произведения ;

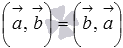2. свойство дистрибутивности 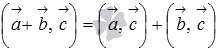или ;

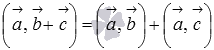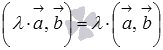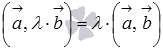3. сочетательное свойство или , где - произвольное действительное число;

4. скалярный квадрат вектора всегда не отрицателен , причем 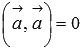тогда и только тогда, когда вектор нулевой.

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения . По определению и . В силу свойства коммутативности операции умножения действительных чисел, справедливо и , тогда . Следовательно, , что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть, и 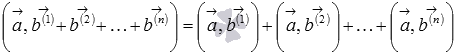, откуда следует

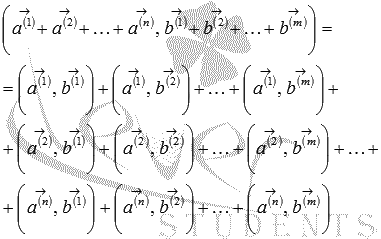
К началу страницы

Вычисление скалярного произведения, примеры и решения.

Решение различных задач на вычисление скалярного произведения векторов сводится к использованию свойств скалярного произведения и формул

1. ;

2. ;

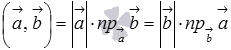3. или ;

4. .

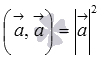Разберем решения наиболее часто встречающихся примеров.

Начнем с самых простых случаев, когда вычисление скалярного произведения производится на основе определения.

Пример.

Вычислите скалярное произведение двух векторов и , если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

Решение.

У нас есть все данные, чтобы вычислить скалярное произведение по определению: .