1.6. Задача экономичного размера заказа с разрывами цен

Представленная в этом разделе модель управления запасами отличается от рассмотренной в разделе 11.3.1 только тем, что продукция может быть приобретена со скидкой, если объем заказа у превышает некоторый фиксированный уровень q; таким образом, стоимость единицы продукции с определяется как

где с₁>с₂. Следовательно,

Используя обозначения из раздела 11.3.1, запишем общие затраты в единицу времени следующим образом.

Графики функций TCU₁ и TCU₂ представлены на рис. 11.3. Так как значения этих функций отличаются только на постоянную величину, то точки их минимума совпадают и находятся в точке

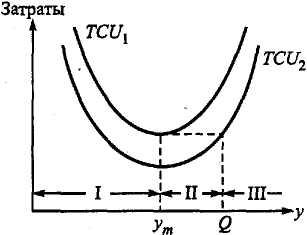
Рис. 11.3

График функции затрат TCU(y), если идти от минимальных значений аргументов, совпадает с графиком функции TCU₁(y) до точки у = q, в которой меняется цена продукции, а затем совпадает с графиком функции ТСU₂(у). Рис. 11.3 показывает, что определение оптимального объема заказа У зависит от того, где находится точка разрыва цены q по отношению к указанным на рисунке зонам I, II и III, которые определены как интервалы [0, у_т), [у_т, Q) и [Q, ∞) соответственно. Величина Q (> у_т) определяется из уравнения

TCU₂(Q)=TCU₁(y_т).

Рис. 11.4 показывает, как определяется оптимальное значение y*.

Алгоритм определения у* можно сформулировать в следующем виде.

Шаг 1. Вычисляем. Еслиqпопадает в зонуI, полагаемy*=y_m. В противвном случае переходим к шагу 2.

Шаг 2. Находим Q из уравнения TCU2(Q) = TCU\(y_m) и определяем зоны II и ИГ Если q находится в зоне II, полагаем у*=q. Иначе q находится в зоне III, тогда у*=у_т.

1.7. Многопродуктовая статическая модель с ограниченной вместимостью склада

Эта модель рассматривает задачу управления запасами п различных товаров, которые хранятся на одном складе ограниченной вместимости. Характер изменения запаса каждого товара в отдельности определяется функцией, показанной на рис. 11.1; предполагаем, что дефицит отсутствует. Отличие от ранее рассмотренных моделей состоит в том, что товары конкурируют между собой за ограниченное складское пространство.

Определим для товара i, i=1,2,...,п, следующие параметры.

D_i — интенсивность спроса,

K_i — стоимость размещения заказа,

h_i — стоимость хранения единицы товара в единицу времени,

у_i — объем заказа,

a_i — необходимое пространство для хранения единицы товара,

А — максимальное складское пространство для хранения товаров п видов.

При отсутствии дефицита математическая модель сформулированной задачи имеет следующий вид.

при ограничениях

у_i >0, i=l,2,…,п.

Алгоритм решения этой задачи можно описать следующим образом.

Шаг 1. Вычисляются оптимальные объемы заказов без учета ограничения по вместимости склада:

Шаг 2. Осуществляется проверка, удовлетворяют ли найденные значения у* ограничению по вместимости склада. Если "Да", вычисления заканчиваются, при этом значения у', /= 1, 2, ..., п являются оптимальными. В противном случае следует перейти к шагу 3.

Шаг 3. Ограничение по вместимости склада должно удовлетворяться в форме равенства. Используется метод множителей Лагранжа для определения оптимальных объемов заказа для задачи с ограничением.

На шаге 3 строится функция Лагранжа

где  (< 0) — множитель Лагранжа.

Так как функция Лагранжа является выпуклой, оптимальные значения y_t и Я находятся из следующих уравнений, которые представляют собой необходимые условия экстремума функции Лагранжа.

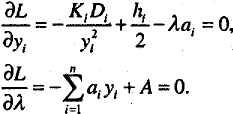
Второе уравнение показывает, что ограничение по вместимости склада в оптимальной точке должно удовлетворяться в форме равенства. Из первого уравнения следует, что

Полученная формула показывает, что у_i* зависит от оптимального значения * множителя Лагранжа. Кроме того, при * = 0 значение у_i* является решением задачи без ограничения.

Значение * может быть найдено следующим образом. Так как по определению в поставленной выше задаче минимизации * < 0, мы последовательно уменьшаем  на достаточно малую величину и используем ее в данной формуле для вычисления соответствующего значения у_i*. Искомое значение * приводит к значениям у_i*, i=1,2,...,n, которые удовлетворяют ограничению по вместимости склада в форме равенства.