13

Лабораторная работа №3

Тема: Управление запасами и вероятностное динамическое программирование.

Цель работы: знакомство с задачами управления запасами и вероятностными задачами динамического программирования, изучение различных методов решения в системе компьютерной математики.

1. Краткие теоретические сведения

1.1 Общая схема решения задач динамического программирования.

Для решения задач динамического программирования необходимо провести ее формализацию, а именно:

1. Определить этапы.

2. Определить на каждом этапе вариантов решения (альтернатив).

3. Определить состояния на каждом этапе.

Из перечисленных выше элементов понятие состояния, как правило, представляется весьма сложным для восприятия. Рассмотренные в этом разделе приложения последовательно показывают, что определение состояния меняется в зависимости от моделируемой ситуации. При рассмотрении каждого приложения полезно ответить на следующие вопросы.

1. Какие соотношения связывают этапы вместе?

2. Какая информация необходима для того, чтобы получить допустимые решения на текущем этапе без повторной проверки решений, принятых на предыдущих этапах?

Далее после формализации применяется какой-нибудь метод решения, например метод обратной прогонки. Далее рассмотрим некоторые виды задач, примеры их формализации и решения.

1.2. Азартная игра

1.2.1. Постановка задачи

Одна из разновидностей игры в русскую рулетку состоит во вращении колеса, на котором по его периметру нанесены п последовательных чисел от 1 доп. Вероятность того, что колесо в результате одного вращения остановится на цифреi, равнар,. Игрок платитх долларов за возможность осуществитьт вращений колеса. Сам же игрок получает сумму, равную удвоенному числу, которое выпало припоследнем вращении колеса. Поскольку игра повторяется достаточно много раз (каждая дот вращений колеса), требуется разработать оптимальную стратегию для игрока.

1.2.2. Формализация задачи

Формализация задачи для динамического программирования сводится к определению этапов, состояний и вариантов решения на каждом этапе. Для данной задачи формализация будет следующей:

Альтернативы	вращать/забрать деньги	забрать/вращать
Состояние	последнее выпавшее число	j
Этап	соответствует i-му вращению колеса	i

Пусть f_i(j) — максимум ожидаемой прибыли при условии, что игра находится на этапе (вращении)iи исходом последнего вращения есть числоj. Имеем следующее:

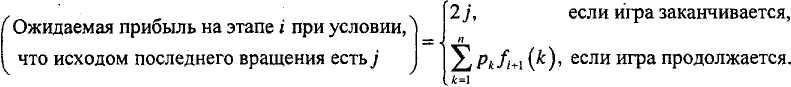
Рекуррентное уравнение для f_i(j) можно записать следующим образом.

Обоснование рекуррентного уравнения сводится к следующему. При первом вращении колеса состоянием системы является, ибо игра только началась. Следовательно,После выполнения последнего вращения колесаимеется лишь один выбор — закончить игру независимо от исходаj т-го вращения. Следовательно,

Рекуррентные вычисления начинаются , заканчиваются прии сводятся таким образом кm+1 вычислительному этапу. Так какf₁(0) представляет собой ожидаемую прибыль от всехm вращений колеса, а игра обходится игроку вх долларов, имеем следующее.

Ожидаемая прибыль = f₁(0) –х.

1.2.3. Метод решения задачи

На каждом этапе составляются матрицы вида:

j	альт-ва 1	…	альт-ва N	fi(j)	Решение
1
…
…
n

В столбце j содержатся состояния. В столбцах альтернатив содержатся возможные выигрыши при выборе данной альтернативы и данном текущем состоянии. Вf_i(j)максимальный выигрыш. В стоблцеРешениеназвание альтернативы, которая дает максимальный результат.

В самом начале выбирается этап для которого нам известно, что будет выбрана одна единственная альтернатива. И далее используя рекурентные соотношения, производится итеративное построение матриц до тех пор пока не будет получена матрица соответствующая последнему рассматриваемому этапу. Ход работы данного метода целесообразно рассмотреть на примере.