Методичка по лабораторной работе №31

1

ЛАБОРАТОРНАЯ РАБОТА №2 ЗАДАЧИ ЛИНЕЙНОГО ПРОГАРММИРОВАНИЯ ТРАСНПОРТНОГО ТИПА

1.Цель работы.

Изучение методов решения задач ЛП транспортного типа.

2. Методы решения

МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА. Выполнение начинается с верхней левой ячейки (севе- ро-западного угла) транспортной таблицы, т.е. с переменной хij.

Шаг 1. Переменной хij присваивается максимальное значение, допускаемое ограничениями на спрос и предложение.

Шаг 2. Вычеркивается строка (или столбец) с полностью реализованным предложением (с удовлетворенным спросом). Это означает, что в вычеркнутой строке (столбце) мы не будем присваивать значения остальным переменным (кроме переменной, определенной на первом шаге). Если одновременно удовлетворяются спрос и предложение, вычеркивается только строка или только столбец.

Шаг 3. Если не вычеркнута только одна строка или только один столбец, процесс останавливается. В противном случае переходим к ячейке справа, если вычеркнут столбец, или к нижележащей ячейке, если вычеркнута строка. Затем возвращаемся к первому шагу.

Пример.

Транспортная компания занимается перевозкой зерна специальными зерновозами от трех элеваторов к четырем мельницам. В табл. 1 показаны возможности отгрузки зерна (предложения) элеваторами (в зерновозах) и потребности (спрос) мельниц (также в зерновозах), а также стоимость перевозки зерна одним зерновозом от элеваторов к мельницам. Стоимость перевозок сij приведена в сотнях долларов.

Таблица 1

В данной задаче требуется определить структуру перевозок между элеваторами и мельницами с минимальной стоимостью. Для этого необходимо найти объемы перевозок xij между i–м элеватором и j–й мельницей.

Таблица 2

2

Соответствующая суммарная стоимость перевозок равна z=5x10+10x2+5x7+15х9+

5х20+10x18 = $520.

МЕТОД НАИМЕНЬШЕЙ СТОИМОСТИ.1 Данный метод находит лучшее начальное решение, чем метод северо-западного угла, поскольку выбирает переменные, которым соответствуют наименьшие стоимости. Сначала по всей транспортной таблице ведется поиск ячейки с наименьшей стоимостью. Затем переменной в этой ячейке присваивается наибольшее значение, допускаемое ограничениями на спрос и предложение. (Если таких переменных несколько, выбор произволен.) Далее вычеркивается соответствующий столбец или строка и соответствующим образом корректируются значения спроса и предложений. Если одновременно выполняются ограничения и по спросу, и по предложению, вычеркивается или строка, или столбец (точно так же, как в методе северо-западного угла). Затем просматриваются невычеркнутые ячейки, и выбирается новая ячейка с минимальной стоимостью. Описанный процесс продолжается до тех пор, пока не останется лишь одна невычеркнутая строка или столбец.

Пример.

Таблица 3

Итерационный алгоритм решения транспортной задачи.

После определения начального решения (с помощью одного из методов, описанных ранее) применяется алгоритм, позволяющий найти оптимальное решение транспортной задачи.

Шаг 1. На основе симплексного условия оптимальности среди текущего множества небазисных переменных определяется вводимая в базис переменная, которая может улучшить значение целевой функции. Если условие оптимальности выполняется для всех небазисных переменных, вычисления заканчиваются, в противном случае необходимо перейти ко второму шагу.

Шаг 2. С помощью симплексного условия допустимости определяется исключаемая из бази-

са переменная. Происходит изменение базиса и возврат к первому шагу.

При изменении базиса в данном случае не используются вычисления, выполняемые при реализации симплекс-метода, — специальная структура транспортной таблицы позволяет значительно упростить вычисления.

Пример

Решим транспортную задачу из примера, используя начальное решение (табл. 4), полученное методом северо-западного угла.

Определение вводимой переменной среди текущих небазисных (т.е. среди тех переменных, которые не входят в начальное базисное решение) основано на вычислении коэффициентов z-строки, соответствующих небазисным переменным, с использованием метода потенциалов (который основан на соотношениях двойственности задачи ЛП).

Таблица 4

3

В методе потенциалов каждой строке i и каждому столбцу j транспортной таблицы ставятся в соответствие числа (потенциалы) иi и vj. Для каждой базисной переменной xij потенциалы иi и vj удовлетворяют уравнению

ui + vj = cij.

В рассматриваемой задаче имеем 7 неизвестных переменных (потенциалов) и 6 уравнений, соответствующих шести базисным переменным. Чтобы найти значения потенциалов из этой системы уравнений, нужно присвоить одному из них произвольное значение (обычно полагают и1=0) и затем последовательно вычислять значения остальных потенциалов.

Таблица 5

Итак, получим

u1 = 0, u2 = 5, u3 = 3,

v1 = 10, v2 = 2, v3 = 4, v4 = 15.

Далее, используя вычисленные значения потенциалов, для каждой небазисной переменной вычисляются величины ui + vj – cij. Результаты вычисления этих величин приведены в следующей таблице.

Таблица 6

Вычисленные значения совместно с нулевыми значениями для базисных переменных (поскольку ui + vj – cij = 0 для любой базисной переменной хij) фактически являются коэффициентами z- строки симплекс-таблицы.

Таблица 7

Поскольку в транспортной задаче ведется поиск минимума стоимости перевозок, вводимой в

базис будет переменная, имеющая наибольший положительный коэффициент в z–строке. В данном случае вводимой переменной будет х31.

Описанные вычисления обычно выполняются непосредственно в транспортной таблице, как показано в табл. 8. В этом случае нет необходимости в явном виде выписывать уравнения для потенциалов. Вычисления в транспортной таблице начинаются с присвоения потенциалу и1 нулевого значения: и1=0. Затем вычисляются v-потенциалы для всех столбцов, имеющих базисные переменные в первой строке. Далее на основании уравнения для потенциалов, соответствующего переменной х22, вычисляется величина потенциала u2. Зная значение потенциала u2, вычисляем по-

4

тенциалы v3 и v4, что позволяет найти потенциал u3. Поскольку все потенциалы определены, далее вычисляются величины иi + vj – cij, для каждой небазисной переменной хij. Эти величины показаны в табл. 8 в левом нижнем углу ячеек транспортной таблицы.

Определив вводимую в базис переменную х31, далее следует определить исключаемую из базиса переменную. Напомним, если какая-либо переменная вводится в базис, одна из текущих базисных переменных должна стать небазисной (и равной нулю), чтобы количество базисных переменных оставалось постоянным (в данном примере количество базисных переменных равняется 3+4–

1=6).

Исключаемая из базиса переменная определяется следующим образом. Выбрав в качестве вводимой переменную х31, мы хотим, чтобы перевозки по маршруту, соответствующему этой переменной, уменьшили общую стоимость перевозок. Какой объем груза можно перевести по этому маршруту? Обозначим через α количество груза, перевозимого по маршруту (3,1) (т.е. x31=α). Максимально возможное значение α определяем из следующих условий.

1.Должны выполняться ограничения на спрос и предложение.

2.Ни по какому маршруту не должны выполняться перевозки с отрицательным объемом грузов.

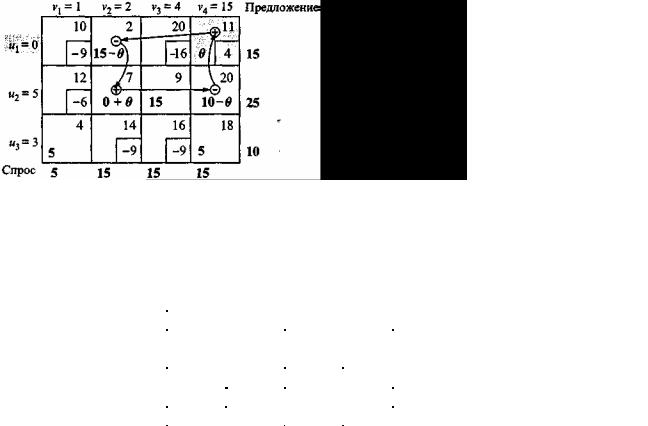
Эти условия позволяют найти значение α и определить исключаемую переменную. Сначала построим замкнутый цикл, который начинается и заканчивается в ячейке, соответствующей вводимой переменной (в данном примере — это ячейка (3,1)). Цикл состоит из последовательности горизонтальных и вертикальных отрезков (но не диагональных), соединяющих ячейки, соответствующие текущим базисным переменным, и ячейку, соответствующую вводимой переменной. В табл. 8 показан цикл для вводимой переменной x31. Для любой вводимой переменной можно построить только один замкнутый цикл.

Теперь найдем значение α. Для того чтобы удовлетворить ограничениям по спросу и предложению, надо поочередно отнимать и прибавлять α к значениям базисных переменных, расположенных в угловых ячейках цикла, как показано в табл. 5.23 (не имеет значения направление обхода цикла: по часовой стрелке или против). Новые значения базисных переменных останутся неотрицательными, если будут выполняться следующие неравенства.

х11 = 5–α ≥0, х22 = 5–α ≥0,

х34 = 10–α ≥0.

Таблица 8

5

Отсюда следует, что наибольшее значение, которое может принять α, равно 5, при этом переменные х11 и х22 обращаются в нуль. Поскольку только одна переменная исключается из базиса, в качестве исключаемой можно выбрать как х11, так и х22 – остановим свой выбор на х22.

Определив значение для вводимой переменной (x31=5) и выбрав исключаемую переменную, далее следует откорректировать значения базисных переменных, соответствующих угловым ячейкам замкнутого цикла, как показано в табл. 9. Поскольку перевозка единицы груза по маршруту (3,1) уменьшает общую стоимость перевозок на $9 (= u3 + v1 — c11), суммарная стоимость перевозок будет на $9x5 = $45 меньше, чем в предыдущем решении. Таким образом, новая суммарная стоимость перевозок будет равна $520 - $45 = $475.

Имея новое базисное решение, следует повторить вычисления потенциалов, как показано в табл. 9. Новой вводимой в базис переменной будет x14. Замкнутый цикл, соответствующий этой переменной, позволяет найти ее значение (x14 = 10) и исключаемую переменную х24.

Таблица 9

Новое решение, показанное в табл. 10, на $4x10 = $40 уменьшает значение целевой функции. Таким образом, новая суммарная стоимость перевозок составляет $475 -$40 = $435. Теперь новые значения величин ui + vj – cij, для всех небазисных переменных xij отрицательные. Поэтому решение, представленное в табл. 10, оптимально.

Таблица 10

Полученное решение, в терминах исходной задачи перевозки зерна от элеваторов до мельниц, имеет следующий смысл.

Таблица 11

Минимальная стоимость всех перевозок равна $435.

6

Транспортная модель с промежуточными пунктами

Транспортная модель с промежуточными пунктами соответствует реальной ситуации, когда между исходными и конечными пунктами перевозок имеются промежуточные пункты для временного хранения грузов (транзитные пункты). Эта модель более общая, чем обычная транспортная, где перевозки осуществляются непосредственно между пунктами отправления и назначения.

В этом разделе показано, как транспортную модель с промежуточными пунктами можно преобразовать (и решить) в обычную транспортную с помощью введения буфера.

Пример 2

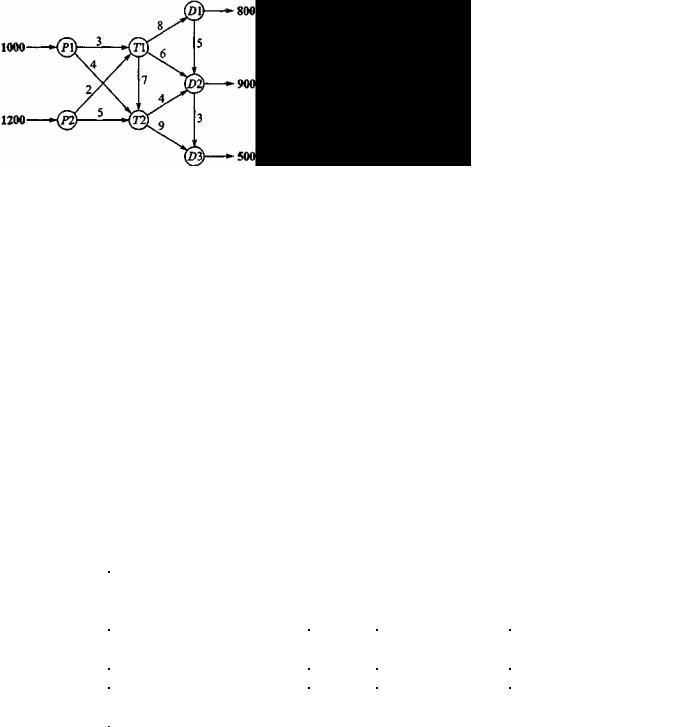
Два автомобильных завода Р1 и Р2 связаны с тремя дилерами Dl, D2 и D3, имеющими два транзитных (перевалочных) центра Т1 и T2, как показано на рис. 5.5. Заводы Р1 и Р2 производят 1000 и 1200 автомобилей. Заказы дилеров составляют соответственно 800, 900 и 300 автомобилей. Стоимость перевозок одного автомобиля (в сотнях долларов) показана на рис.1.

Рис. 1

В данной модели перевозки транзитом могут осуществляться через любые пункты (в соответствии с направлением дуг на схеме), даже через некоторые пункты назначения. Поэтому пункты, которым соответствуют как входящие, так и выходящие дуги на схеме рис. 5.5, назовем транзитными (пункты T1, T2, D1 и D2). Оставшиеся будут либо истинными пунктами отправления (пункты Р1 и Р2 либо истинными пунктами назначения (в данной схеме такой пункт только один — D3). Эту модель можно преобразовать в обычную транспортную модель с шестью пунктами отправления (Р1, Р2, Т1, T2, D1 и D2) и пятью пунктами назначения (T1, T2, D1, D2 и D3). Объемы спроса и предложения, соответствующие этим пунктам отправления и назначения, вычисляются следующим образом.

Объем предложения истинного пункта отправления = объем исходного предложения. Объем предложения транзитного пункта = объем исходного предложения + объем буфера.

Объем спроса истинного пункта назначения = объем исходного спроса. Объем спроса транзитного пункта = объем исходного спроса + объем буфера.

Объем буфера должен быть таким, чтобы вместить объем всего предложения (или спроса). Обозначим через В объем буфера. Тогда

В = Общий объем предложения (или спроса)=1000 + 1200 = = (или = 800 + 900 + 500) = 2200 автомобилей.

Построенная транспортная модель, эквивалентная исходной задаче, представлена в табл.11.

Таблица 11

7

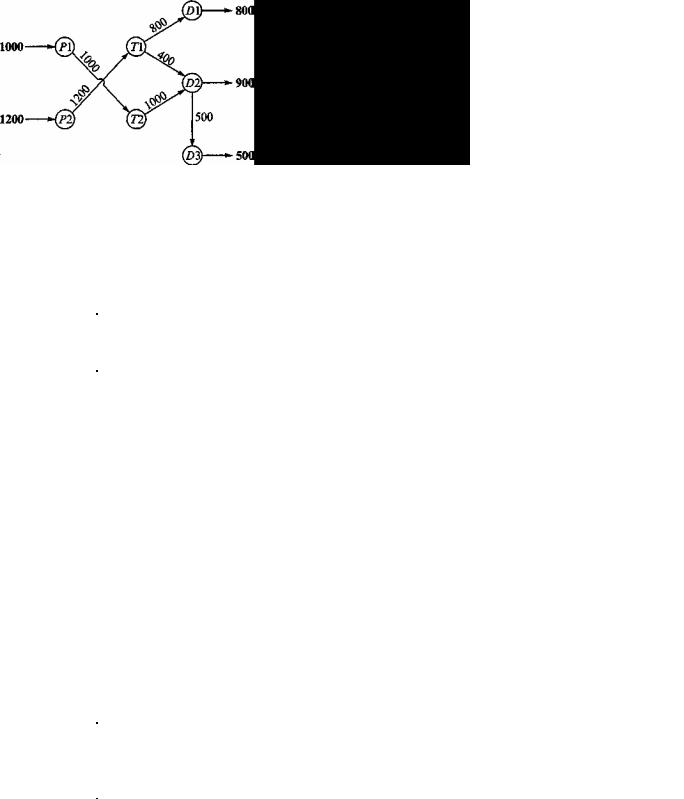
Решение этой транспортной модели (полученное с помощью программы TORA) показано на рис. 2. Отметим "транзитный" эффект решения: дилер D2 получает 1400 автомобилей, из них 900 оставляет себе (для удовлетворения своего спроса), а 500 отправляет дилеру D3.

Рис. 2

3.Варианты задания

1. Три электрогенерирующие станции мощностью 25, 40 и 30 миллионов кВт/ч поставляют электроэнергию в три города. Максимальная потребность в электроэнергии этих городов оценивается в 30, 35 и 25 миллионов кВт/ч. Цены за миллион кВт/ч в данных городах показаны в табл. 5.6.

В августе на 20% возрастает потребность в электроэнергии в каждом из трех городов. Недостаток электроэнергии города могут восполнить из другой электросети по цене $1000 за 1 миллион кВт/ч. К сожалению, третий город не может подключиться к альтернативной электросети. Электрогенерирующие станции планируют разработать наиболее экономичный план распределения электроэнергии и восполнения ее недостатка в августе.

a) Сформулируйте эту задачу в виде транспортной модели.

b)Решите транспортную задачу и определите оптимальный план распределения электроэнергии электрогенерирующими станциями.

c)Определите стоимость дополнительной электроэнергии для каждого из трех городов.

2.Выполните предыдущее упражнение в предположении, что 10% электроэнергии теряется при передаче по электросетям.

3.Управление национальными парками получило четыре заявки от подрядчиков на лесозаготовки в трех сосновых лесных массивах Арканзаса. Эти массивы имеют площадь 10 000, 20 000 и 30 000 акров. Каждый подрядчик может получить для разработки не более половины всех отводимых для лесозаготовки площадей. Предлагаемые подрядчиками цены за разрешение на лесозаготовки показаны в табл. 5.7.

a)В описанной ситуации необходимо максимизировать общую прибыль, получаемую управлением национальными парками. Покажите, как эту проблему можно представить в виде транспортной задачи.

b)Определите площади, выделяемые каждому подрядчику для лесозаготовок.

8

4. Три нефтеперегонных завода с ежедневной производительностью 6, 5 и 8 миллионов галлонов бензина снабжают три бензинохранилища, ежедневная потребность которых составляет 4, 8 и 7 миллионов галлонов бензина соответственно. Бензин транспортируется в бензинохранилища по бензопроводу. 'Стоимость транспортировки составляет 10 центов за 1000 галлонов на 1 милю длины трубопровода. В табл. приведены расстояния (в милях) между заводами и хранилищами. Отметим, что первый нефтеперегонный завод не связан трубопроводом с третьим бензинохранилищем.

a)Сформулируйте транспортную задачу.

b)Найдите оптимальную схему транспортировки бензина.

5. Пусть в предыдущем упражнении ежедневная производительность третьего нефтеперерабатывающего завода составляет 6 миллионов галлонов бензина, а потребности первого бензинохранилища должны выполняться в обязательном порядке. Кроме того, на недопоставки бензина во второе и третье хранилища накладываются штрафы в размере 5 центов за каждый недопоставленный галлон бензина.

a)Сформулируйте соответствующую транспортную задачу.

b)Решите сформулированную задачу и найдите оптимальную схему поставок бензина.

6.Пусть в задании 4 ежедневные потребности третьего бензинохранилища составляют 4 миллиона галлонов. Избыток своей продукции первый и второй нефтеперегонные заводы могут отправить на другие бензохранилища с помощью автотранспорта. В этом случае транспортные расходы на транспортировку 100 галлонов бензина составляют $1.50 и $2.20 для первого и второго заводов соответственно. Третий нефтеперерабатывающий завод может использовать свои излишки бензина для нужд собственного химического производства.

a)Сформулируйте соответствующую транспортную задачу.

b)Решите сформулированную задачу и найдите оптимальную схему поставок бензина.

7.Три плодовых хозяйства поставляют апельсины в ящиках четырем оптовым покупателям. Ежедневная потребность этих покупателей составляет 150, 150,400 и 100 ящиков соответственно. Предположим, что все три плодовых хозяйства используют только постоянную рабочую силу и могут ежедневно поставлять 150, 200 и 250 ящиков апельсинов соответственно. Первые два хозяйства могут увеличить поставки апельсинов путем привлечения дополнительных рабочих, третье хозяйство такой возможности не имеет. Транспортные расходы на один ящик апельсинов приведены в следующей табл.

a)Сформулируйте соответствующую транспортную задачу.

b)Решите сформулированную задачу.

c)Сколько дополнительных ящиков апельсинов могут поставить первое и второе хозяйства, используя временных рабочих?

8.Три распределительных центра поставляют автомобили пяти дилерам. Автомобили от распределительных центров к дилерам перевозятся на трейлерах, и стоимость перевозок пропорциональна расстоянию между пунктами отправления и назначения и не зависит от степени загрузки трейлера. В следующей таблице приведены расстояния между распределительными центрами и дилерами, а также соответствующие величины спроса и предложения, выраженные в количествах автомоби-

9

лей. При полной загрузке трейлер вмещает 18 автомобилей. Транспортные расходы составляют $25 на одну милю пути, пройденного трейлером.

a)Сформулируйте соответствующую транспортную задачу.

b)Решите сформулированную задачу.

9.Компания MG Auto производит четыре модели автомобилей. Завод в Детройте выпускает модели Ml, М2 и М4. Модели Ml и М2 производятся в Новом Орлеане, МЗ и М4 — в Лос-Анджелесе. Производительность каждого завода и потребности распределительных центров в автомобилях разных моделей даны в таблице

Расстояния между заводами и распределительными центрами приведены в следующей таблице, транспортные расходы составляют 8 центов за перевозку одного автомобиля (любой модели) на одну милю пути.

Кроме всего прочего, есть возможность удовлетворить спрос на одну из моделей автомобилей за счет другой в соответствии с таблицей

a)Сформулируйте соответствующую транспортную задачу.

b)Решите сформулированную задачу.

(Совет. Введите четыре новых пункта назначения, соответствующих комбинациям (М1,М2), (МЗ, М4), (М1,М2) и (М2, М4). Величины потребностей новых пунктов назначения определяются на основании данных о процентном соотношении заменяемых моделей автомобилей.)

10. Компания планирует оптимизировать распределение станочного парка, состоящего из станков четырех типов, для выполнения станочных работ пяти видов. Пусть имеется 25, 30, 20 и 30 станков каждого типа. Приведем количество работ каждого вида: 20, 20, 30, 10 и 25 соответственно. Отметим, что станки четвертого типа не используются для выполнения работ четвертого вида. В следующей таблице представлена стоимость (в долларах) выполнения каждого вида работ на станках определенного типа. Сформулируйте транспортную задачу, решите ее и интерпретируйте полученный результат.

11. Спрос на некий скоропортящийся продукт в следующие 4 месяца составляет 400, 300, 420 и 380 тонн соответственно. Предложение этого товара в те же месяцы составляет 500, 600, 200 и 300 тонн. Отпускная цена на этот товар колеблется от месяца к месяцу и равна соответственно $100, $140, $120 и $150 за тонну. Поскольку товар скоропортящийся, он должен быть реализован в течение трех месяцев (включая текущий). Стоимость хранения в течение месяца тонны товара равна

$3.

Природа товара такова, что невозможна задержка с выполнением заказа. Опишите данную ситуацию как транспортную модель и найдите ее оптимальное решение.

12.Спрос на специализированные малые двигатели в следующие пять кварталов составляет 200, 150, 300, 250 и 400 единиц. Мощность производства двигателей в тот же период времени оценивается в 180, 230, 430, 300 и 300 единиц. Невыполнение заказов не допускается, при необходимости можно организовать сверхурочные работы для выпуска дополнительной продукции. Стоимость единицы продукции в каждый из следующих пяти кварталов составляет $100, $96, $116, $102 и $106 соответственно. Стоимость дополнительно произведенной продукции увеличивается на 50% по сравнению со "стандартной" стоимостью в соответствующий период. Если двигатели, произведенные в одном квартале, реализуются в последующих, за хранение одного двигателя в течение квартала необходимо заплатить $4. Сформулируйте транспортную задачу. Определите оптимальный план производства двигателей.

13.Периодически проводится профилактика самолетных двигателей с заменой важной детали А. В следующие 6 месяцев будут выполнены регламентные работы (с разбивкой по месяцам) на 200, 180, 300, 198, 230 и 290 двигателях. Все регламентные работы, запланированные на месяц, проводятся в течение первых двух дней месяца, когда производится замена отработанной детали А на новую или отремонтированную. Снятая деталь может быть отремонтирована в местной ремонтной мастерской, где она будет готова к началу следующего месяца, или отправлена в центральные мастерские, откуда она вернется через 3 месяца (считая месяц, в котором выполнены профилактические работы). Стоимость ремонта одной детали А в местной мастерской составляет $120, а в центральной— только $35. Если отремонтированная деталь будет использована в последующие месяцы, стоимость ее хранения составит $1.50 в месяц. Новые детали можно купить по цене $200 в первом месяце с возрастанием цены на 5% каждые 2 месяца. Представьте описанную ситуацию в виде транспортной модели и найдите ее оптимальное решение.

14. В транспортной сети, показанной на рис. 1, осуществляются перевозки из пунктов 1 и 2 в пункты 5 и 6 через транзитные пункты 3 и 4. Стоимость перевозок показана на этом же рисунке.

a)Постройте транспортную модель с промежуточными пунктами и соответствующую ей обычную транспортную модель.

b)Решите транспортную задачу с помощью программы TORA и покажите на схеме маршруты доставки грузов из пунктов отправления в пункты назначения.

Рис.1

15.Пусть в предыдущей задаче пункты 1 и 2 связаны транспортной магистралью со стоимостью