Лабораторная работа №2
.docМИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО НАУКЕ И ОБРАЗОВАНИЮ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Лабораторная работа №2
Задачи линейного программирования транспортного типа.
Выполнил:
студент гр. АСОИ-231
Проверил: Насыров Р.В.
Уфа-2007
Задачи линейного программирования транспортного типа.
1.Цель работы
Изучение методов решения задач ЛП с помощью процедур СКМ MATH CAD. Исследование чувствительности решения. Построение графических изображений задачи.
2. Интерпретация метода потенциалов как симплекс-метода
Связь метода потенциалов с симплекс-методом основывается на соотношениях двойственности задач ЛП. Исходя из специальной структуры транспортной задачи, двойственная ей задача будет в следующем виде.
Максимизировать z = aiui +bjvj
При ограничениях
Ui и Vj-свободные переменные
Ai-предложение пункта отправления i
Bj-спрос пункта назначения j
Cij-стоимость перевозки единицы груза из пункта отправления I в пункт назначения j
Ui- двойственная переменная, соответствующая ограничению на предложение пункта отправления i
Vj-двойственная переменная, соответствующая ограничению на спрос пункта назначения j
Из соотношений двойственности следует, что коэффициент при переменной xij в выражении целевой функции должен быть равен разности между левой и правой частями соответствующею ограничения двойственной задачи, т.е. величине ui+vj=cij. Но как мы уже знаем, эта величина должна быть равной нулю для каждой базисной переменной. Другими словами, для этих переменных должно выполняться равенство u+v=c Имея m+n-1 таких равенств и решая их как систему линейных уравнений, находим значения потенциалов u и v. Вычислив значения потенциалов, далее определяем вводимую к базис переменную среди всех небазисных как переменную, имеющую наибольшее положительное значение величины u+v-c.
3. Задача
Три электрогенерирующие станции мощностью 25, 40 и 30 миллионов кВт/ч поставляют электроэнергию в три города. Максимальная потребность в электроэнергии этих городов оценивается в 30, 35 и 25 миллионов кВт/ч. Цены за миллион кВт/ч в данных городах показаны в табл. 5.6.
Город
1 2 3
|
$600 |
$700 |
$400 |
|
$320 |
$300 |
$350 |
|
$500 |
$480 |
$450 |
Станция 2
3
В августе на 20% возрастает потребность в электроэнергии в каждом из трех городов.
Выполните упражнение в предположении, что 10% электроэнергии теряется при передаче по электросетям
Недостаток электроэнергии города могут восполнить из другой электросети по цене $1000 за 1 миллион кВт/ч. К сожалению, третий город не может подключиться к альтернативной электросети. Электрогенерирующие станции планируют разработать наиболее экономичный план распределения электроэнергии и восполнения ее недостатка в августе
b) Решите транспортную задачу и определите оптимальный план распределения электроэнергии электрогенерирующими станциями
с) Определите стоимость дополнительной электроэнергии для каждого из трех городов.
4. Решение
1)
|
600 |
700 |
400 |
|
320 |
300 |
350 |
|
500 |
480 |
450 |
Станция 36
27 30 35 25
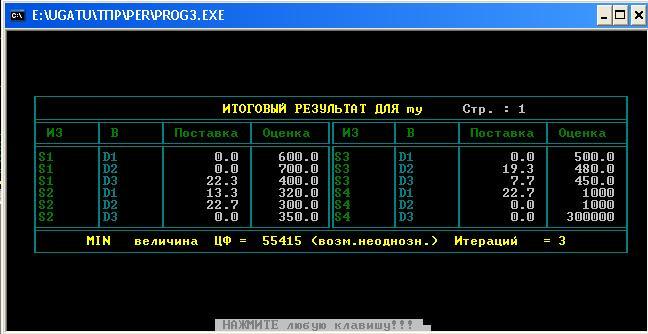
 Город
Город
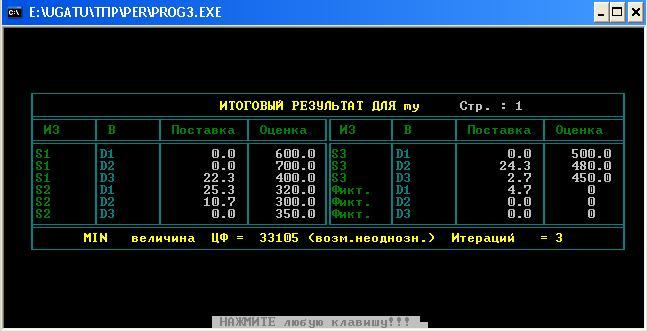
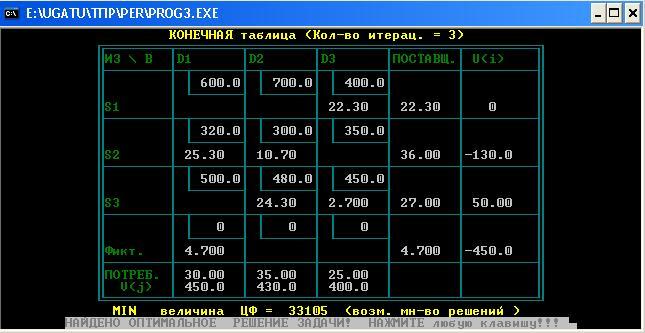
2)дополнительная станция
|
600
|
700 |
400 |
|
320
|
300 |
350 |
|
500
|
480 |
450 |
|
1000 |
1000 |
300000 |
22,3
36
Станция
27
22,7 36 42 30
Город