Лабораторная работа №1

МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО НАУКЕ И ОБРАЗОВАНИЮ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Лабораторная работа №1

Задачи линейного программирования

Выполнил:

студент гр. АСОИ-231

.

Проверил: Насыров Р.В.

Уфа-2007

Цель работы.

Изучение методов решения задач ЛП с помощью процедур СКМ MathCAD.Построение графических изображений задач.

Задание к работе

Задача 4

Тихоокеанская бумажная фабрика производит стандартные рулоны бумаги шириной в 20 футов. Специальные заказы клиентов требуют разрезания стандартных рулонов. Типовой заказ (такие заказы могут меняться каждый день)

приведен в следующей таблице.

Позиции рулона заказа	Требуемая ширина (футы)	Требуемое кол-во рулонов (шт.)
1	5	150
2	7	200
3	9	300

На фабрике заказы выполняются путем разрезания стандартных рулонов на требуемые специальными ножами. Существует несколько вариантов разрезки стандартного рулона, три из которых показаны на рис. 2.14. Конечно, существуют и другие варианты, не показанные на этом рисунке (они будут описаны ниже), но сейчас мы ограничимся только представленными — А, В и С. Для выполнения заказа можно совместно использовать несколько вариантов разрезки стандартных рулонов. Например, для выполнения заказа, приведенного в таблице, можно применить следующие комбинации вариантов А, В и С.

1. Разрезать 300 стандартных рулонов, используя вариант А, и 75 рулонов с помощью варианта В.

2. Разрезать 200 стандартных рулонов, используя вариант А, и 100 рулонов с помощью варианта С.

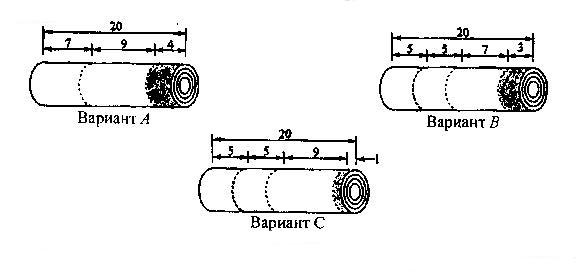
Рис. 2.14. (Размеры даны в футах)

Какая из этих комбинаций лучше? Чтобы ответить на этот вопрос, надо рассмотреть потери от каждой из комбинаций. На рис. 2.14 серым цветом показаны отходы бумаги после каждого варианта разрезки. Мы можем оценить преимущества каждой комбинации, если подсчитаем суммарные отходы, полученные после их применения. Но поскольку отрезки рулонов, идущие в отходы, имеют разную длину, нам надо подсчитать объем этих отходов, а не просто количество отрезков. Предполагая, что стандартный рулон бумаги имеет площадь поперечной сечения, равную L квадратным футам, подсчитываем потери для комбинаций 1 и 2 (рис 2.14).

Комбинация 1: 300х(4 х L) + 75х(3 x L) = 14251 куб. футов. Комбинация 2: 200х(4хL) + 100x(1 х L) = 900I куб. футов.

Если число рулонов шириной 5, 7 или 9 футов, которые были получены в результате применения какой-либо комбинации вариантов разрезки, превышает количество, необходимое для выполнения заказа, то разность между ними также следует отнести к потерям В первой комбинации при использовании варианта А получено 300 - 200 = 100 лишних рулонов шириной 7 футов; применение варианта В добавляет еще 75 лишних рулонов такой же ширины. Таким образом, дополнительные потери составляют 175 x (7 х L) = 225L куб. футов. Комбинация 2 не производит лишних рулонов шириной 7 и 9 футов, но применение варианта С приводит к появлению 200 -150=50 лишних рулонов шириной 5 футов, что составляет 50 х (5 х L) = 250L куб. футов дополнительных отходов бумаги. В результате этих выкладок имеем следующее.

Объем отходов от комбинации 1 = 1425L + 1225L = 2650.L куб. футов. Объем отходов от комбинации 2 = 900L + 2501 - 11501 куб. футов.

Очевидно, что комбинация 2 лучше, так как имеет меньше отводов.

Для получения оптимального решения данной задачи необходимо определить допустимые варианты разрезки стандартных рулонов и затем получить все комбинации этих вариантов. Хотя определить все допустимые варианты разрезки несложно, перебор всех комбинаций этих вариантов уже является нетривиальной задачей. Здесь необходим систематический подход к организации такого перебора. В данном случае это может выполнить задача линейного программирования.

Решение задачи линейного программирования

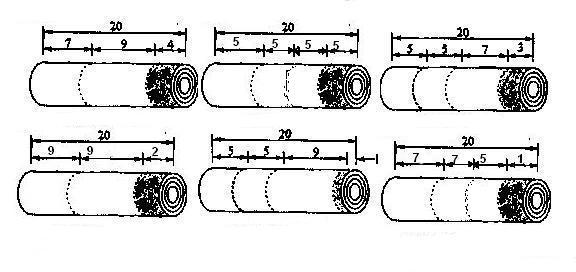
x₁,x₂,x₃,x₄,x₅,x₆-количество рулонов нарезанных каждым из 6 способов

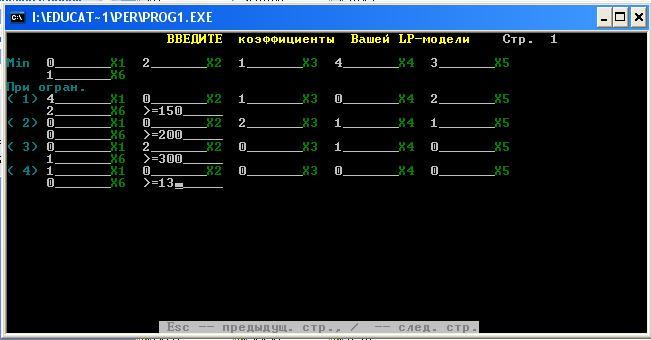
f(x₁,x₂,x₃,x₄,x₅,x₆):=0x₁+2x₂+1x₃+4x₄+3x₅+1x₆

Ограничивающие условия:

4x₁+1x₃+2x₅+2x₆>=150;

2x₃+1x₄+1x₅>=200;

2x₂+1x₄+1x₆>=300;

x₁>=13;

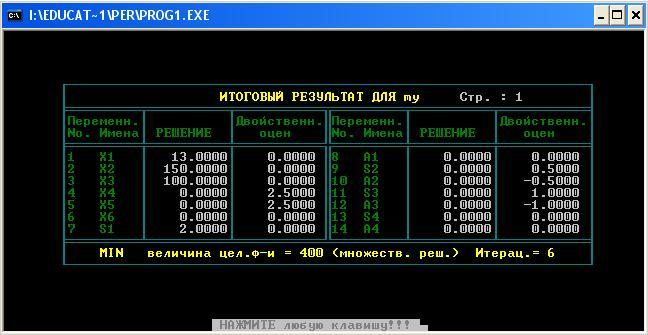
R:=Minimize f(x₁,x₂,x₃,x₄,x₅,x₆)