
- •Введение
- •1. Предмет теории игр.
- •3.1. Задачи линейного программирования.
- •3.2. Построение экономико-математических моделей задач линейного программирования.
- •3.3. Графическое решение задачи линейного программирования.
- •4.1 Алгоритм симплекс-метода.
- •5. Методы нахождения опорного решения задачи линейного программирования.
- •5.1. Метод искусственного базиса.
- •5.2. Второй алгоритм отыскания опорного плана.
- •6. Двойственные задачи линейного программирования.
- •6.1. Взаимодвойственные задачи.
- •7. Сведение матричной игры к двойственной задаче линейного программирования.
- •7.1. Сведение задачи линейного программирования к матричной игре.
Введение
Каждый человек ежедневно, не всегда осознавая это, решает проблему: как получить наибольший эффект, обладая ограниченными средствами. Наши средства и ресурсы всегда ограничены. Жизнь была бы менее интересной, если бы это было не так. Не трудно выиграть сражение, имея армию в 10 раз большую, чем у противника. Чтобы достичь наибольшего эффекта, имея ограниченные средства, надо составить план, или программу действий. Раньше план в таких случаях составлялся “на глазок” (теперь, впрочем, зачастую тоже). В середине XX века был создан специальный математический аппарат, помогающий это делать “по науке”. Соответствующий раздел математики называется математическим программированием. Слово “программирование” здесь и в аналогичных терминах (“линейное программирование, динамическое программирование” и т.п.) обязано отчасти историческому недоразумению, отчасти неточному переводу с английского. По-русски лучше было бы употребить слово “планирование”. С программированием для ЭВМ математическое программирование имеет лишь то общее, что большинство возникающих на практике задач математического программирования слишком громоздки для ручного счета, решить их можно только с помощью ЭВМ, предварительно составив программу. Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Леонида Витальевича Канторовича “Математические методы организации и планирования производства”. Поскольку методы, изложенные Л.В.Канторовичем, были мало пригодны для ручного счета, а быстродействующих вычислительных машин в то время не существовало, работа Л.В.Канторовича осталась почти не замеченной.
Цель курсовой работы изучить метод сведения матричной игры к задаче линейного программирования, решения задачи с помощью симплекс-метода, нахождение алгоритмов решения, и реализация их на языке программирования.
Работа состоит из введения, семи частей, заключения и приложения, в котором приведена программа на языке Turbo Pascal, позволяющая находить приближённое решение задачи линейного программирования.
В работе рассмотрены основные понятия теории игр и линейного программирования. Так же рассмотрены алгоритмы симплекс-метода и сведение к нему матричной игры, имеет место и обратный процесс сведения задачи линейного программирования к матричной игре.
1. Предмет теории игр.
Теория игр – это теория математических моделей принятия оптимальных решений в условиях конфликта или неопределённости. При этом конфликт не обязательно должен быть антагонистическим, в качестве конфликта можно рассматривать любое разногласие.
Рассмотрим следующий экономический пример. Пусть требуется принять решение о выпуске на рынок некоторого товара. Может случиться, что объём спроса на этот товар известен точно; может быть, что известно лишь статистическое распределение возможных значений спроса; наконец, может оказаться, что известны лишь границы, в которых заключен спрос, но ни каких даже вероятностных соображений о его предстоящих значениях нет. Последний случай квалифицируется как неопределённость. Такая неопределённость может возникнуть, когда спрос (например, на сезонные товары) зависит от метеорологических условий (конфликт с природой) или в условиях рынка от деятельности конкурента, уже удовлетворившего неизвестную часть спроса. Приведённые примеры при определённых условиях могут быть приведены к игре.
Всякая теоретико-игровая модель должна отражать, кто и как конфликтует, а также, кто и в какой форме заинтересован в том или ином исходе конфликта.
Действующие в конфликте стороны называются игроками, а решения, которые способны принимать игроки, стратегии.
Содержание математической теории игр состоит, во-первых, в установлении принципов оптимального поведения игроков в играх, во-вторых, в доказательстве существования ситуации, которые складываются в результате применения этих принципов, и, в-третьих, в разработке методов фактического нахождения таких ситуаций.
Для игр с одной коалицией действия множество всех ситуаций можно принять за множество стратегий этой единственной коалиции действия и далее о стратегиях не упоминать. По этому такие игры называются нестратегическими, важным классом которых являются игры с природой, применяемые для анализа экономических ситуаций, оценки эффективности принимаемых решений и выбора наиболее предпочтительных альтернатив, в которых риск связан с совокупностью неопределённых фактов окружающей среды, именуемых «природа». Поэтому термин «природа» характеризует некоторую объективную действительность, которую не следует понимать буквально, хотя вполне могут встретиться ситуации в которых игроком действительно может выступить природа (например, обстоятельства, связанные с погодными условиями или с природными стихийными силами).
В отличие от нестратегических игр, все остальные игры с двумя или более коалициями действия называются стратегическими. В практических ситуациях часто появляется необходимость согласования действий компании, объединений, министерств и других участников проектов в случаях, когда их интересы не совпадают. В подобных ситуациях теория стратегических игр позволяет найти оптимальное решение для поведения всех участников проекта, обязанных согласовывать свои действия при столкновении интересов.
Далее будут
рассмотрены матричные игры. Под матричной
игрой
![]() понимается такая игра двух игроков, при
которой каждый игрок имеет конечное
число возможных ходов – чистых стратегий.
При этом выигрыш одного игрока и проигрыш
другого при применении ими определённых
чистых стратегий выражается числом.
Перечисленные условия позволяют записать
стратегии в матрицу
понимается такая игра двух игроков, при
которой каждый игрок имеет конечное
число возможных ходов – чистых стратегий.
При этом выигрыш одного игрока и проигрыш
другого при применении ими определённых
чистых стратегий выражается числом.
Перечисленные условия позволяют записать
стратегии в матрицу
![]() (1.1)
(1.1)
где
![]() – равен выигрышу первого (будем обозначать
его А) и проигрышу второго (игрока В) при
применении имиi-й
и j-й
чистых стратегий соответственно.
– равен выигрышу первого (будем обозначать
его А) и проигрышу второго (игрока В) при
применении имиi-й
и j-й
чистых стратегий соответственно.
Задачей теории игр является определение оптимальных стратегий игроков. В матричной игре оптимальной для игрока А называется стратегия, которая при многократном повторении игры обеспечивает максимально возможный средний выигрыш, а для игрока В под оптимальной понимается стратегия, обеспечивающая ему минимальный средний проигрыш. При этом предполагается, что противник является по меньшей мере таким же разумным и делает всё для того, чтобы помешать нам добиться своей цели.
Нижняя и верхняя цены игры. Принцип минимакса.
Итак, рассмотрим
матричную игру
![]() с платежной матрицей
с платежной матрицей
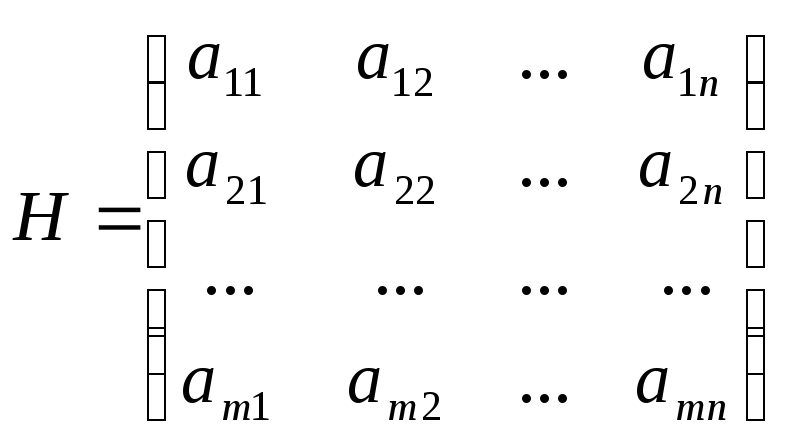 (1.2)
(1.2)
Где i-я строка соответствует Аi-й стратегии игрока А;
j-й столбец соответствует Вj-й стратегии игрока В.
Пусть игрок А
выбирает некоторую стратегию Аi,
тогда в
наихудшем случае (например, если выбор
станет известен игроку В) он получит
выигрыш равный
![]() .
Предвидя эту возможность, игрок А должен
выбрать такую стратегию, чтобы
максимизировать свой минимальный в
каждой стратегии выигрыш
.
Предвидя эту возможность, игрок А должен
выбрать такую стратегию, чтобы
максимизировать свой минимальный в
каждой стратегии выигрыш![]() .
Таким образом,
.
Таким образом,![]() .
Величина
.
Величина![]() называется нижней ценой игры (
называется нижней ценой игры (![]() – это гарантированный выигрыш игрока
А).
– это гарантированный выигрыш игрока
А).
Очевидно,
![]() находится в одной из строк матрицы Н,
пусть вi0,
тогда стратегия
находится в одной из строк матрицы Н,
пусть вi0,
тогда стратегия
![]() называется максиминной.
называется максиминной.
Итак, если игрок
А будет придерживаться максиминной
стратегии, то ему при любом поведении
игрока В гарантируется выигрыш, во
всяком случае не меньше
![]() .
.
С другой стороны,
противник – игрок В, заинтересован в
том, чтобы обратить выигрыш игрока А в
минимум, поэтому он должен пересмотреть
каждую свою стратегию с точки зрения
максимального выигрыша игроком А при
этой стратегии. Другими словами, при
выборе некоторой стратегии Bj
он должен
исходить из максимального проигрыша в
этой стратегии, равного
![]() ,
и найти такую стратегию, при которой
этот проигрыш будет наименьшим, то есть
не более чем
,
и найти такую стратегию, при которой
этот проигрыш будет наименьшим, то есть
не более чем![]() .
.
Величина
![]() называется верхней ценой игры, а
соответствующая ему стратегия
называется верхней ценой игры, а
соответствующая ему стратегия![]() – минимаксной.
– минимаксной.
Принцип осторожности, диктующий игрокам выбор стратегий максиминной или минимаксной соответственно, в теории игр именуют принципом минимакса, а сами стратеги максиминные и минимаксные – общим термином минимаксные стратегии.
Рассмотрим пример
нахождения
![]() и
и![]() .
.
Пример (п.1.1)
Пусть игра задана матрицей
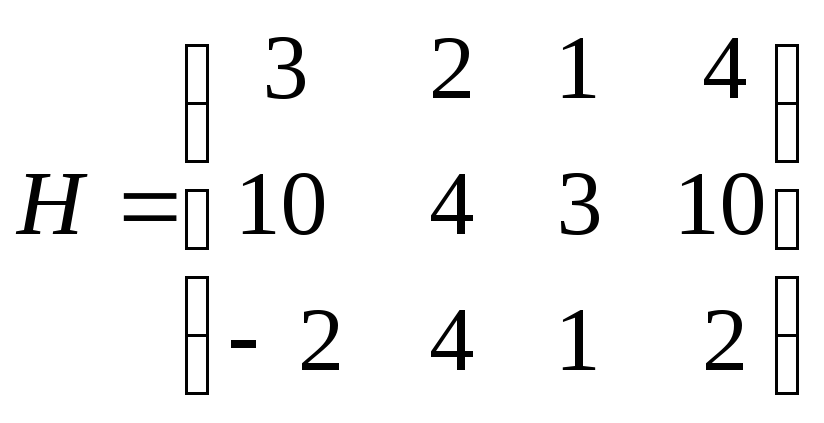
Определим нижнюю и верхнюю цены игры.
Выпишем для каждой
строки справа от матрицы
![]() ,
а снизу
,
а снизу![]() каждого столбца. Тогда получим:
каждого столбца. Тогда получим:
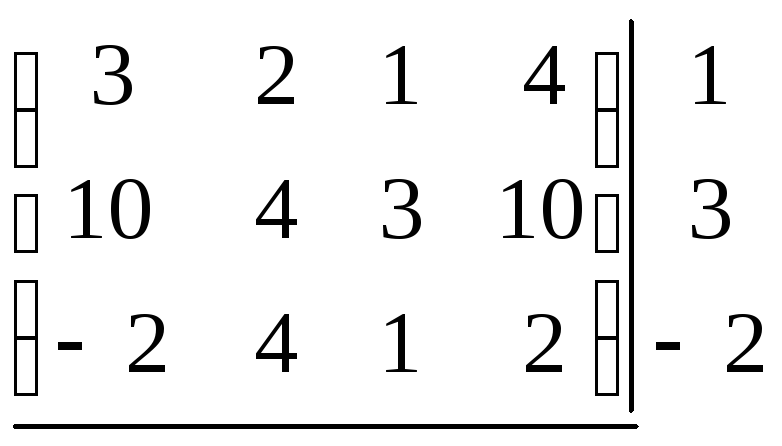
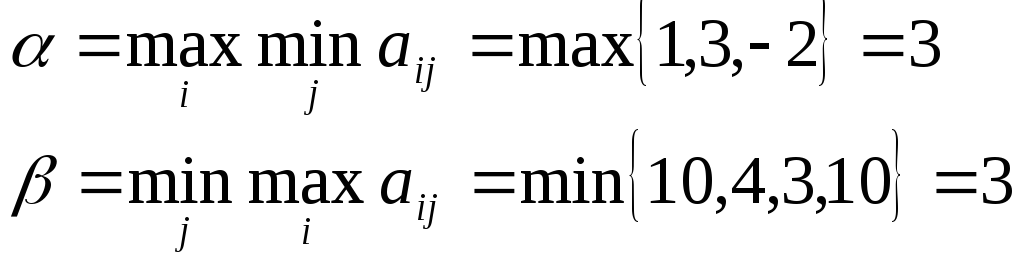
10 4 3 10
В этом примере нижняя и верхняя цены игры совпадают:
![]()
Вполне определённые игры.
Вполне определённая игра является наиболее простым случаем матричной игры. Вполне определённой игрой или игрой с седловой точкой называется игра, у которой совпадают нижняя и верхняя цены игры, то есть выполняется равенство:
![]() (1.3)
(1.3)
При этом
![]() называется ценой игры, элемента
называется ценой игры, элемента![]() соответствующий равенству, называют
седловой точкой.
соответствующий равенству, называют
седловой точкой.
Простота решения
игры с седловой точкой заключается в
том, что оптимальные стратегии обоих
игроков находятся сразу. Для игрока А
это стратегия
![]() для
игрока В –
для
игрока В –![]() .
Причём, такое решение обладает свойством
устойчивости в том смысле, что если один
из игроков применяет свою оптимальную
стратегию, то любое отклонение другого
игрока от оптимальной стратегии может
оказаться не выгодным для него.
.
Причём, такое решение обладает свойством
устойчивости в том смысле, что если один
из игроков применяет свою оптимальную
стратегию, то любое отклонение другого
игрока от оптимальной стратегии может
оказаться не выгодным для него.
Действительно,
пусть игрок А выбрал оптимальную
стратегию соответствующую
![]() ,
то есть игрок А обеспечивает себе выигрыш
, равный одному из элементов
,
то есть игрок А обеспечивает себе выигрыш
, равный одному из элементов![]() строки, причём, элемент в
строки, причём, элемент в![]() столбце наименьший среди них
столбце наименьший среди них![]() .
И если игрок В выберетj-ю
стратегию отличную от
.
И если игрок В выберетj-ю
стратегию отличную от
![]() ,
то он проиграет сумму, равную
,
то он проиграет сумму, равную![]() ,
а игрок А соответственно выиграет её.
Аналогичные рассуждения показывают не
выгодность стратегии, отличной от
оптимальной, для игрока А, когда В
придерживается своей оптимальной
стратегии.
,
а игрок А соответственно выиграет её.
Аналогичные рассуждения показывают не
выгодность стратегии, отличной от
оптимальной, для игрока А, когда В
придерживается своей оптимальной
стратегии.
Решением игры в
примере (п.1.1) (1.3) является выбор стратегий
![]() игроком
игроком![]() и
и![]() игроком
игроком![]() ,
при этом цена игрыV
= 3.
,
при этом цена игрыV
= 3.
Игры, не содержащие седловой точки. Смешанные стратегии.
Среди конечных
игр, имеющих практическое значение,
сравнительно редко встречаются игры с
седловой точкой. Более типичным является
случай, когда нижняя и верхние цены не
совпадают
![]() ,
причём, не трудно показать, что тогда
,
причём, не трудно показать, что тогда![]() .
.
Действительно,
пусть
![]() ,
это означает, что вk-й
строке элемент
,
это означает, что вk-й
строке элемент
![]() наименьший, то есть при нахождении
наименьший, то есть при нахождении![]() в их число попадут значения не меньшие
в их число попадут значения не меньшие![]() ,
так как даже в этой строке элементы в
других столбцах больше или равны
,
так как даже в этой строке элементы в
других столбцах больше или равны![]() .
Значит, и
.
Значит, и
![]() .
(1.4)
.
(1.4)
Откуда следует,
что
![]() ,
но мы рассматриваем случай
,
но мы рассматриваем случай![]() ,
значит
,
значит![]() .
Итак, в играх, не имеющих седловой точки,
нижняя цена игры
.
Итак, в играх, не имеющих седловой точки,
нижняя цена игры![]() всегда меньше верхней
всегда меньше верхней![]() .
.
Установленный
факт означает, что если игра одноходовая,
то есть партнёры играют один раз, выбирая
по одной чистой стратегии, то в расчёте
на разумно играющего противника они
должны придерживаться принципа минимакса,
это гарантирует выигрыш
![]() игроку А и проигрыш
игроку А и проигрыш![]() игроку В. Следовательно, при применении
минимаксных стратегий величина платежаV
ограничена неравенством
игроку В. Следовательно, при применении
минимаксных стратегий величина платежаV
ограничена неравенством
![]() .
(1.5)
.
(1.5)
Если же игра повторяется не однократно, то постоянное применение минимаксных стратегий становится не разумным. Например, если игрок В будет уверен в том, что на следующем ходу А применит прежнюю стратегию, то он несомненно выберет стратегию, отвечающую наименьшему в это строке, а не прежнюю.
Таким образом, мы пришли к выводу, что при неоднократном повторении игры обоим игрокам следует менять свои стратегии. Тогда возникает вопрос: а каким образом их менять, чтобы в среднем выигрыш одного и проигрыш другого был аналогично одноходовой игре, ограничиваясь снизу и сверху соответственно?
Для ответа на этот
вопрос введём вероятность (относительную
частоту)
![]() применение игроком Аi-й
стратегии, и
применение игроком Аi-й
стратегии, и
![]() – вероятность примененияj-й
стратегии игроком В. Совокупности этих
вероятностей определяют векторы
– вероятность примененияj-й
стратегии игроком В. Совокупности этих
вероятностей определяют векторы
![]() ,
где
,
где![]() и
и![]() ,
где
,
где![]() .
.
Эти векторы или наборы вероятностей выбора чистых стратегий называются смешанными стратегиями игроков.
В частности, решение
игры с седловой точкой даётся векторами
![]() и
и![]() ,
среди компонент которых
,
среди компонент которых![]() ,
,![]()
![]() и
и![]() ,
,![]()
![]() .
.
Для получения ограничений на средний выигрыш или проигрыш рассмотрим математическое ожидание выигрыша первого игрока
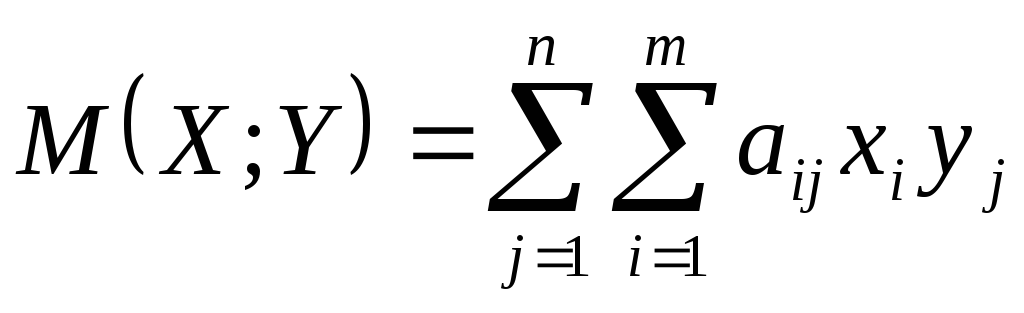 .
(1.6)
.
(1.6)
Если второй игрок
В выбрал некоторую смешанную стратегию
![]() ,
то первому игроку, естественно, считать
лучшей ту смешанную стратегию
,
то первому игроку, естественно, считать
лучшей ту смешанную стратегию![]() ,
при которой достигается
,
при которой достигается
![]() :
:
![]() .
(1.7)
.
(1.7)
Аналогично, при
выборе первым игроком некоторой стратегии
![]() второму игроку следует выбирать стратегию
второму игроку следует выбирать стратегию![]() такую,
что
такую,
что
![]() .
(1.8)
.
(1.8)
Ясно, что
![]() зависит от
зависит от![]() и
и![]() зависит от
зависит от![]() .
Перед каждым игроком, таким образом,
возникает задача выбора оптимальной
стратегии, под которой для игрока А
понимается смешанная стратегия
.
Перед каждым игроком, таким образом,
возникает задача выбора оптимальной
стратегии, под которой для игрока А
понимается смешанная стратегия![]() ,
которая максимизирует математическое
ожидание его выигрыша, для игрока В –
стратегия
,
которая максимизирует математическое
ожидание его выигрыша, для игрока В –
стратегия![]() ,
минимизирующая математическое ожидание
его проигрыша.
,
минимизирующая математическое ожидание
его проигрыша.
Основная теорема теории игр (доказана фон Нейманом в 1928 году) утверждает:
Каждая матричная
игра с нулевой суммой имеет, по крайней
мере, одно решение, возможно в области
смешанных стратегий, то есть существуют
стратегии
![]() и
и![]() ,
оптимальные для обоих игроков, причём
,
оптимальные для обоих игроков, причём
![]() .
(1.9)
.
(1.9)
Число
![]() называют ценой игры.
называют ценой игры.
Примечание. Нулевая сумма означает, что выигрыш одного игрока равен проигрышу другого.
Из основной теоремы следует, что каждая конечная игра имеет цену и она лежит между нижней и верхней ценами игры (1.8).
И, если один из игроков придерживается своей оптимальной стратегии, то выигрыш (проигрыш) его остаётся неизменным независимо от тактики другого игрока, если, конечно, последний не выходит за пределы своих «полезных» стратегий, иначе выигрыш (проигрыш) возрастает.
Это означает выполнение неравенств
![]()
![]() ,
(1.10)
,
(1.10)
![]() ,
,![]() .
(1.11)
.
(1.11)
Примечание. Эти неравенства будут необходимы при сведении матричной игры к задаче линейного программирования.
Элементарные методы решения матричных игр
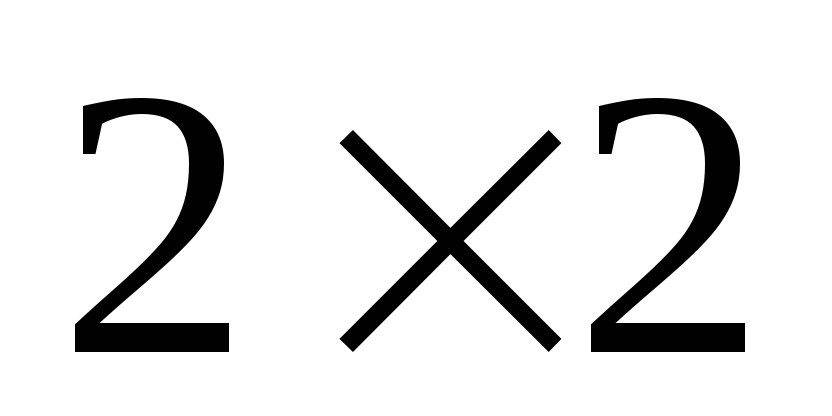 ,
,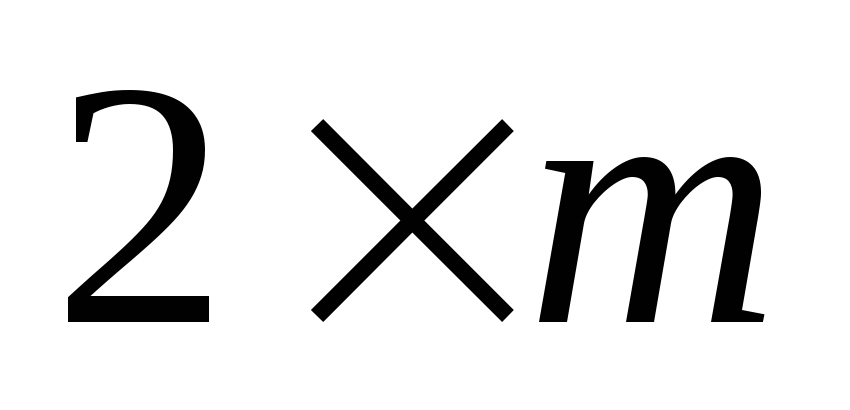 ,
,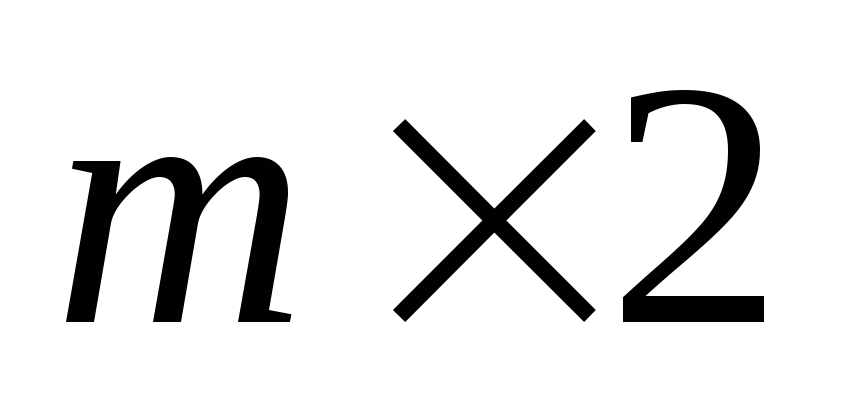 .
.
Игра
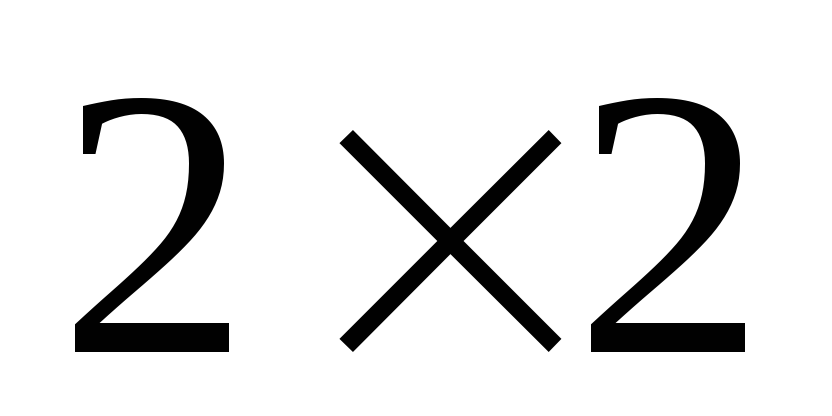 .
.
Наиболее простой
матричной игрой является игра
![]() ,
в которой игроки имеют по две чистых
стратегии.
,
в которой игроки имеют по две чистых
стратегии.
Пусть матрица такой игры
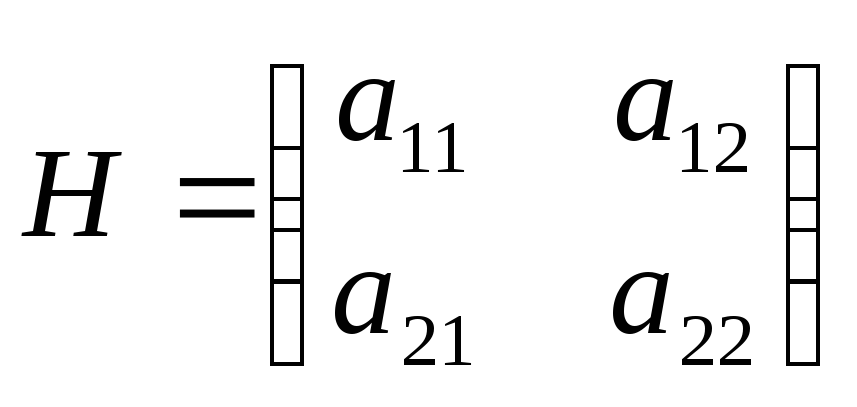 .
(2.1)
.
(2.1)
Если седловой
точки нет, то решением игры являются
смешанные стратегии
![]() (2.2)
(2.2)
![]() .
(2.3)
.
(2.3)
С
При стратегии В1
игрока В,
При стратегии В2
игрока В.![]() игроком А обеспечивает получение
выигрышаV
при любых стратегиях игрока В. Сказанное
приводит к системе уравнений:
игроком А обеспечивает получение
выигрышаV
при любых стратегиях игрока В. Сказанное
приводит к системе уравнений:
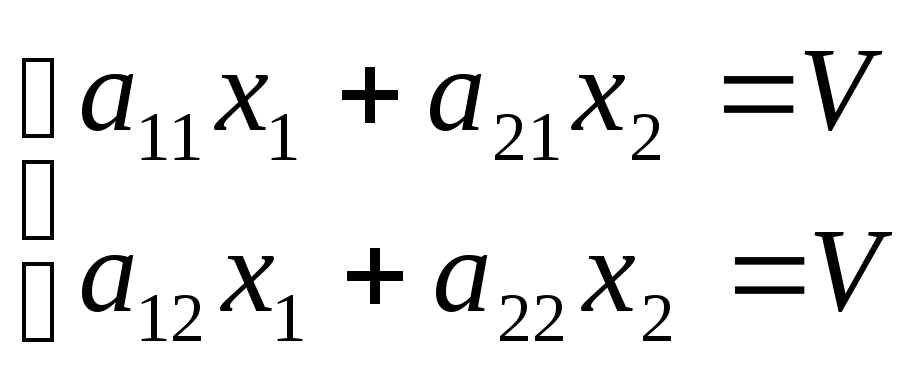
Кроме того,
![]() .
.
Решение этих уравнений даёт:
![]() ,
(2.4)
,
(2.4)
![]() ,
(2.5)
,
(2.5)
![]() .
(2.6)
.
(2.6)
Аналогично,
применение оптимальных стратегии
![]() обеспечивает проигрышV
игроку В при любых стратегиях А, что
приводит к системе
обеспечивает проигрышV
игроку В при любых стратегиях А, что
приводит к системе
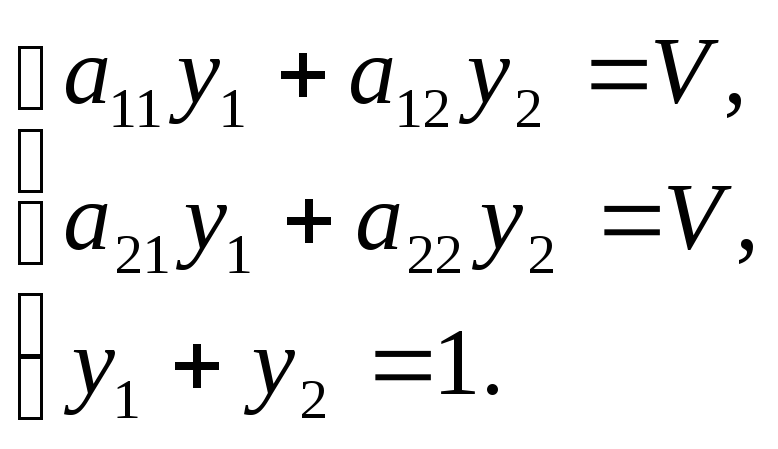 (2.7)
(2.7)
Ее решение даётся формулами
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
Пример (п.2.1)
Во многих учебниках приводится пример игры в «орла и решку», суть которой состоит в следующем. Каждый из двух партнёров, не зная хода другого, кладёт свою монету орлом или решкой вверх и при совпадении наименований второй игрок (В) платит первому (А) единицу, а при несовпадении первый платит второму. Очевидно платёжная матрица такой игры будет:
![]()
Седловой точки нет. Тогда, согласно формул: (2.4), (2.5), (2.6), (2.8) и (2.9), оптимальными стратегиями будут
![]() ,
,
![]() ,
цена игры
,
цена игры![]() .
.
Примечание.
Отмечу, что матрица этой игры симметрична
и на первый взгляд может показаться,
что симметричность матрицы ведёт к
справедливой (безобидной) игре для обоих
игроков. На самом деле симметричность
не гарантирует справедливости, напротив,
кососимметричные матрицы (когда
![]() )
соответствуют совершенно справедливой
игре, то есть при оптимальных стратегиях,
как это легко установить, цена игры
)
соответствуют совершенно справедливой
игре, то есть при оптимальных стратегиях,
как это легко установить, цена игры![]() .
.
Пример (п.2.2)
Цех заготовитель поставляет в сборочный цех детали двух видов a и b. По договору между цехами оговорены ежедневно два срока поставки этих деталей, причём, при поставке в первый срок деталей вида «а» сборочный цех платит заготовительному премию 50 руб., при поставке же изделий «а» выплачивается премия 20 руб. При поставке же изделий вида «b» в первый срок премия составляет 30 руб., а во второй – 40 руб. Определить оптимальные стратегии поставок и получения деталей.
Решение. Принимая цех-заготовитель за игрока А, а сборочный за В, составим матрицу игры.
Таблица 2.1
Матрица игры заданная таблицей
|
|
I срок |
II срок |
|
Детали «а» Детали «b» |
50 30 |
20 40 |
Значит,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
следовательно, седловой точки нет. Для
нахождения оптимальных стратегий
применим формулы (2.4), (2.5), (2.6), (2.8) и (2.9):
,
следовательно, седловой точки нет. Для
нахождения оптимальных стратегий
применим формулы (2.4), (2.5), (2.6), (2.8) и (2.9):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() (руб.).
(руб.).
Таким образом,
цех-изготовитель поставляет детали
вида а и b
с вероятностями
![]() ,
,![]() ,
при этом гарантированная премия 35
рублей, а сборочный цех получает эти
детали в срокиI
и II
с вероятностями
,
при этом гарантированная премия 35
рублей, а сборочный цех получает эти
детали в срокиI
и II
с вероятностями
![]() ,
,![]() и выплачивает 35 рублей премии
заготовительному цеху ежедневно.
Полученные вероятности и определяют
оптимальные стратегии
и выплачивает 35 рублей премии
заготовительному цеху ежедневно.
Полученные вероятности и определяют
оптимальные стратегии
![]() ,
,
![]() .
.
Примечание.
Игры
![]() допускают простое графическое толкование
и решение, следующее из него. Действительно,
пусть игра задана матрицей (2.1). На оси
абсцисс отложим отрезок 0D,
равный 1, и условимся считать, что левый
конец отрезка
допускают простое графическое толкование
и решение, следующее из него. Действительно,
пусть игра задана матрицей (2.1). На оси
абсцисс отложим отрезок 0D,
равный 1, и условимся считать, что левый
конец отрезка
![]() – стратегии А2,
тогда промежуточная точка N
с координатой x
соответствует некоторой смешанной
стратегии первого игрока, причём,
– стратегии А2,
тогда промежуточная точка N
с координатой x
соответствует некоторой смешанной
стратегии первого игрока, причём,
![]() ,
,![]() ,
так как при
,
так как при![]() имеем
имеем![]() и
и![]() ,
и при
,
и при![]() имеем
имеем![]() и
и![]() .
.
Вводя ось 0y,
можно построить прямую, отвечающую
стратегии второго игрока, её уравнение
![]() (при каждомx,
y
даёт значение выигрыша игрока А, когда
В применяет стратегию В1).
Отметим, что для построения В1
достаточно
провести из концов отрезка 0D
прямые, не перпендикулярные ему, на
левой прямой отложить
(при каждомx,
y
даёт значение выигрыша игрока А, когда
В применяет стратегию В1).
Отметим, что для построения В1
достаточно
провести из концов отрезка 0D
прямые, не перпендикулярные ему, на
левой прямой отложить
![]() ,
на правой –
,
на правой –![]() и, соединив их получим прямую В1В1,
отвечающую
стратегии В1
рис. 2.1. Затем аналогично строим стратегию
В2 (её
уравнение
и, соединив их получим прямую В1В1,
отвечающую
стратегии В1
рис. 2.1. Затем аналогично строим стратегию
В2 (её
уравнение
![]() ).
Заметим , что при каждомx
точки на прямых В1В1
и В2В2
отвечают
выигрышем первого игрока при применении
вторым игроком стратегий В2
и В1
соответственно.
Откуда следует, что ломаная
В2КВ1
рис. 2.2
отвечает нижней границе выигрыша игрока
А, а значит в точке её максимума, то есть
цена игры
).
Заметим , что при каждомx
точки на прямых В1В1
и В2В2
отвечают
выигрышем первого игрока при применении
вторым игроком стратегий В2
и В1
соответственно.
Откуда следует, что ломаная
В2КВ1
рис. 2.2
отвечает нижней границе выигрыша игрока
А, а значит в точке её максимума, то есть
цена игры
![]() и точкаN
отвечает оптимальной стратегии игрока
А:
и точкаN
отвечает оптимальной стратегии игрока
А:
![]()
![]() .
.
Для нахождения оптимальной стратегии игрока В, исходя из графика, можно воспользоваться формулами:
![]() ;
(2.10)
;
(2.10)
![]() .
(2.11)
.
(2.11)
В справедливости
формул (2.10) и (2.11) легко убедиться,
подставив значения LB2
и LB1,
![]() ,
,![]() и значение
и значение![]() ,
тогда получим формулы, совпадающие с
(2.10) и (2.11).
,
тогда получим формулы, совпадающие с
(2.10) и (2.11).
Аналогично, меняя ролями x и y, можно построить решение для игрока А.
a21 x 0 x D D 0
B1(50)
B1(30)
B2(40)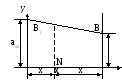
![]()
![]()

рис. 2.1. Графическое рис. 2.2. Графическое
толкование
игры
![]() толкование игры
толкование игры![]()
Решение игры
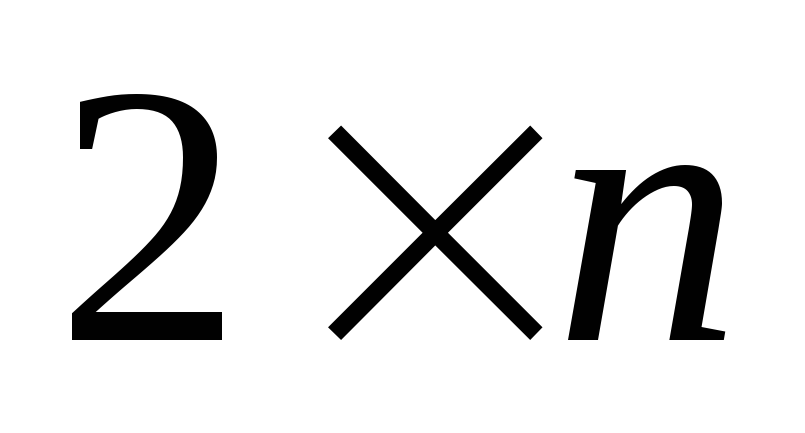 .
.
Пусть игра задана матрицей
![]() .
.
Строим прямые, соответствующие стратегиям игрока В рис. 2.3.
Ломаная
![]() соответствует нижней границе выигрыша,
точка К на ней даёт решение игры:
соответствует нижней границе выигрыша,
точка К на ней даёт решение игры:![]() ,
,![]() ,
,![]() .
.
В данном случае
оптимальная стратегия противника
получается применением смеси двух
полезных стратегий
![]() и
и![]() ,
пересекающихся в точке К. Стратегия
,
пересекающихся в точке К. Стратегия![]() является заведомо выгодной при оптимальных
стратегиях.
является заведомо выгодной при оптимальных
стратегиях.
![]() ,
,
![]() .
.
0 0
![]()
![]()

рис. 2.3. Иллюстрация рис. 2.4. Иллюстрация
решения
игры
![]() решения игры
решения игры
![]()
Решение игры
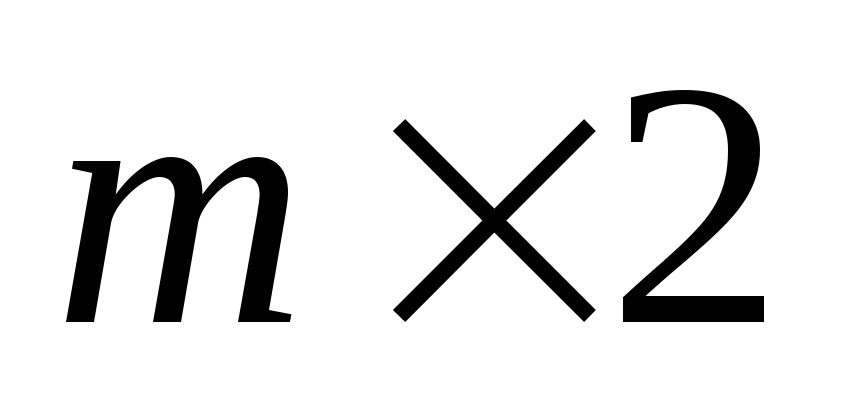 .
.
Аналогично может
быть решена игра с матрицей
![]() ,
только в этом случае строим верхнюю
границу выигрыша и на ней определяем
минимум.
,
только в этом случае строим верхнюю
границу выигрыша и на ней определяем
минимум.
Пусть игра задана матрицей
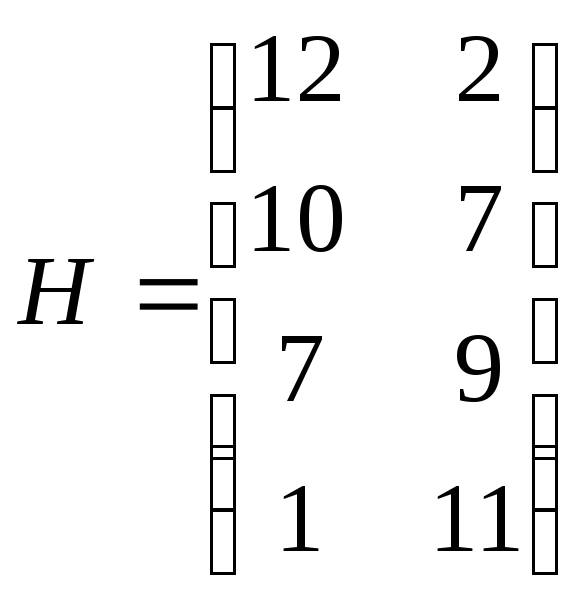 .
.
Решение задачи находим для игрока В рис. 2.4.
Ломаная
![]() изображает верхнюю границу выигрыша
игрока А, на ней ищется точка К с
минимальной ординатой, которая и есть
цена игры
изображает верхнюю границу выигрыша
игрока А, на ней ищется точка К с
минимальной ординатой, которая и есть
цена игры![]() ,
,![]() ,
,![]() .
.
Оптимальными стратегиями для игрока А являются вторая и третья. При этом
![]() ,
,
![]() .
.
Матрица оптимальных
стратегий имеет вид
![]() .
Тогда решение можно найти по формулам
(2.4), (2.5), (2.6), (2.8) и (2.9).
.
Тогда решение можно найти по формулам
(2.4), (2.5), (2.6), (2.8) и (2.9).
Следовательно, решение игры таково:
![]() ,
,
![]() ,
,![]() .
.
Решение матричных игр
 .
.
При решении
произвольной конечной игры размера
![]() рекомендуется придерживаться следующей
схемы:
рекомендуется придерживаться следующей
схемы:
1. Исключить из платёжной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами заведомо меньшими (большими) по сравнению с элементами других строк (столбцов).
2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена игры совпадает с верхней (нижней) ценой.
3. Если седловая
точка отсутствует, то решение следует
искать в смешанных стратегиях. Для игр
размера
![]() рекомендуется симплексный метод, а для
игр размером
рекомендуется симплексный метод, а для
игр размером
![]() ,
,![]() ,
,![]() следует руководствоваться выводами
предыдущих пунктов.
следует руководствоваться выводами
предыдущих пунктов.
Пример (п.2.3)
Магазин может
завести в различных пропорциях товары
четырёх типов
![]() .
Их реализация и прибыль магазина зависят
от вида товара и состояния спроса.
.
Их реализация и прибыль магазина зависят
от вида товара и состояния спроса.
Предполагается,
что спрос может иметь пять состояний
![]() и не прогнозируется. Определить
оптимальные пропорции в закупке товаров
из условия максимизации средней
гарантируемой прибыли, при следующей
матрице прибыли табл. 2.2.
и не прогнозируется. Определить
оптимальные пропорции в закупке товаров
из условия максимизации средней
гарантируемой прибыли, при следующей
матрице прибыли табл. 2.2.
Таблица 2.2
Матрица прибыли
|
Тип товара |
Спрос | ||||
|
В1 |
В2 |
В3 |
В4 |
В5 | |
|
А1 А2 А3 А4 |
200 300 400 700 |
400 400 500 300 |
600 600 600 500 |
400 500 500 200 |
700 800 800 100 |
Будем рассматривать
возникшую ситуацию как игровую. Сторона
А стремится увеличить прибыль, а потому
для неё стратегия
![]() заведомо выгодна по сравнению со
стратегией
заведомо выгодна по сравнению со
стратегией![]() .
Точно так же стратегия
.
Точно так же стратегия![]() уступает стратегии
уступает стратегии![]() ,
и исходные данные упрощаются табл. 2.3.
,
и исходные данные упрощаются табл. 2.3.
Для игрока В
естественным является выбор стратегии
с большим спросом. Поэтому стратегия
![]() менее выгодна, чем стратегия
менее выгодна, чем стратегия![]() ,
в свою очередь, стратегия
,
в свою очередь, стратегия![]() невыгодна по сравнению со стратегией
невыгодна по сравнению со стратегией![]() .
.
Таблица 2.3 Таблица 2.4
Матрица игры заданная таблицей Матрица игры заданная таблицей
|
В
А |
В1 |
В2 |
В3 |
В4 |
В5 | ||||||||
|
А3 А4 |
400 700 |
500 300 |
600 500 |
500 200 |
800 100 | ||||||||
|
|
|
|
|
| |||||||||
|
|
|
|
|
| |||||||||
|
В
А |
В1 |
В3 |
В5 |
|
А3 А4 |
400 700 |
600 500 |
800 100 |
Пример (п.2.4)
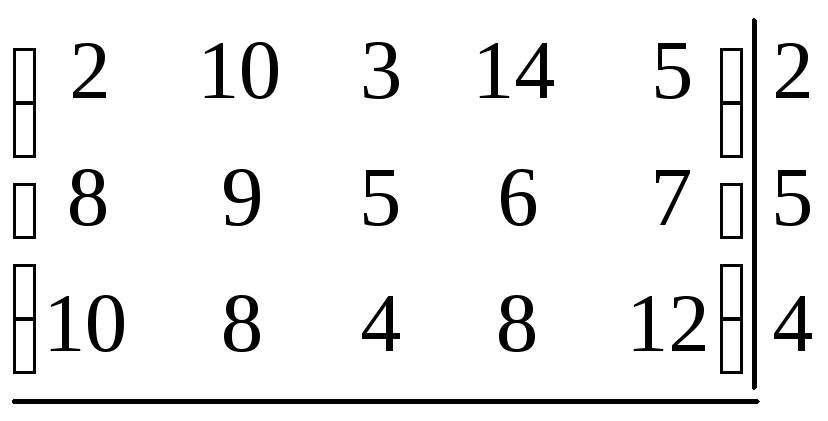
Предполагается оснастить цех новой технологической линией. Промышленность выпускает три типа линий. На каждой из линий можно изготовлять пять различных видов изделий. Учитывая расходы сырья, трудоёмкость, спрос и др., составлена матрица предполагаемой прибыли
 .
.
Нужно выбрать тип технологической линии, при которой прибыль будет наибольшей.
![]()
![]()
Так как
![]() ,
то игра имеет седловую точку и задача
разрешима в чистых стратегиях. Выбирая
второй тип технологической линии, будет
достигнута наибольшая прибыль не меньше
пяти.
,
то игра имеет седловую точку и задача
разрешима в чистых стратегиях. Выбирая
второй тип технологической линии, будет
достигнута наибольшая прибыль не меньше
пяти.
Линейное программирование.
Оптимизационная задача – это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причём значения переменных должны принадлежать некоторой области допустимых значений.
В самом общем виде задача математически записывается так:
![]() ;
;
![]() ,
(3.1)
,
(3.1)
где
![]() ;
;
![]() –область допустимых
значений переменных
–область допустимых
значений переменных
![]() ;
;
![]() –целевая функция.
–целевая функция.
Для того чтобы
решить задачу оптимизации, достаточно
найти её оптимальное решение, т.е. указать
![]() такое, что
такое, что![]() при любом
при любом![]() ,
или для случая минимизации
,
или для случая минимизации![]() при любом
при любом![]() .
.
Оптимизационная
задача является неразрешенной, если
она не имеет оптимального решения. В
частности, задача максимизации будет
неразрешима, если целевая функция
![]() не ограничена сверху на допустимом
множестве
не ограничена сверху на допустимом
множестве![]() .
.
Методы решения
оптимизационных задач зависят как от
вида целевой функции
![]() ,
так и от строения допустимого множества
,
так и от строения допустимого множества![]() .
Если целевая функция в задаче является
функцией
.
Если целевая функция в задаче является
функцией![]() переменных, то методы решения называются
методами математического программирования.
переменных, то методы решения называются
методами математического программирования.
В математическом
программировании принято следующие
основные задачи в зависимости от вида
целевой функции
![]() и от области
и от области![]() :
:
1. Задачи линейного
программирования, если
![]() и
и![]() линейны.
линейны.
2. Задачи целочисленного
программирования, если ставится условие
целочисленности переменных
![]() .
.
3. Задачи не линейного
программирования, если форма
![]() носит не линейный характер.
носит не линейный характер.
