6. Двойственные задачи линейного программирования.

6.1. Взаимодвойственные задачи.

Рассмотрим задачу об использовании ресурсов. Пусть предприятие №1 производит видов продукции и используетвидов сырья. Известна прибыль, получаемая с единицы продукции,. Известны технологические коэффициенты ,, Требуется организовать производство так, чтобы предприятию была обеспечена максимальная прибыль.

Таблица 6.1

Исходные данные

Цены на ресурсы	Запасы сырья	Продукция
		П1	П2		Пn
	Прибыль с единицы продукции

Запишем в общем виде экономико-математическую модель задачи об использовании ресурсов. Для этого введём переменные ,– количество продукцииj-го вида. Тогда ограничения на сырье запишутся в виде

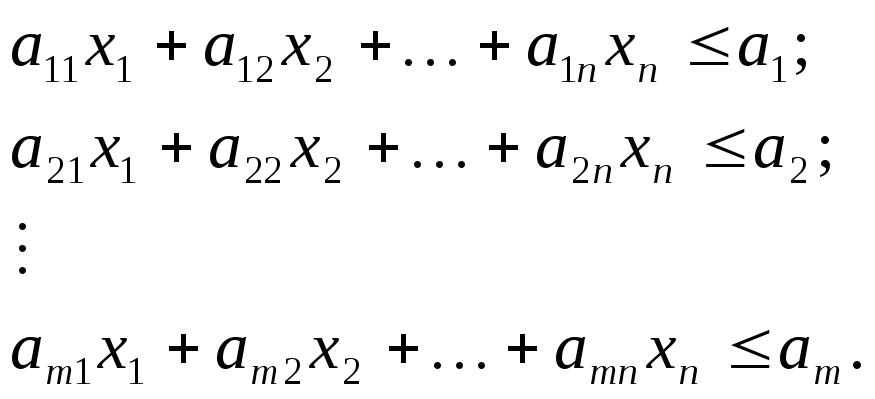(6.1)

Целевая функция, определяющая максимум прибыли, имеет вид

; (7.2)

, .

По этим же исходным данным сформулирую задачу по предприятию №2.

Допустим, предприятие №2 решило закупить все ресурсы, которыми располагает предприятие №1. В этом случае предприятию №2 необходимо установить оптимальные цены на эти ресурсы, исходя из следующих условий:

1) общая стоимость ресурсов для предприятия №2 должна быть минимальной;

2) за каждый вид ресурса предприятию №1 надо уплатить не менее той суммы, которую это предприятие может получить при переработке данного вида ресурса в готовую продукцию.

Обозначу цены, по которым предприятие №2 покупает ресурсы у предприятия №1, через ,. Запишу экономико-математическую модель для предприятия №2 с учётом вышеуказанных условий 1) и 2).

Целевая функция, определяющая минимальную суммарную стоимость ресурсов, имеет вид

. (6.3)

В соответствии с условием 2) запишем систему ограничений:

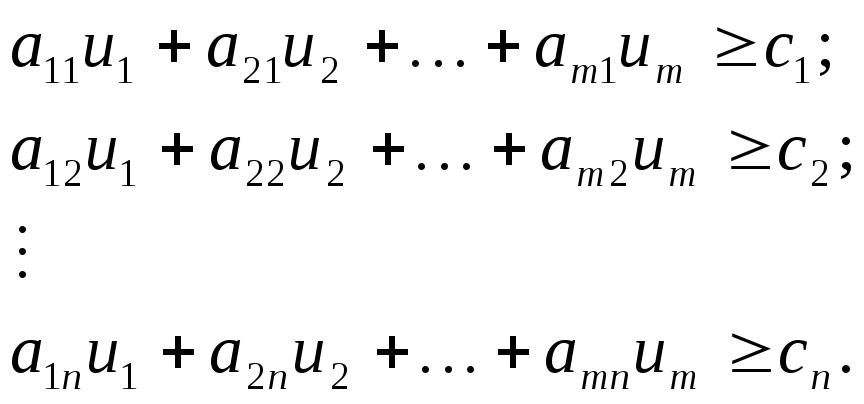(6.4)

Сравню математические модели задач (6.1), (6.2) и (6.3), (6.4):

1) число неизвестных одной задачи равно числу ограничений другой задачи;

2) матрица коэффициентов системы ограничений получается одна из другой путём транспортирования;

3) неравенства в системах ограничений имеют противоположный смысл;

4) свободные члены системы ограничений одной из задач становится коэффициентами целевой функции другой задачи, коэффициенты целевой функции превращаются в свободные члены ограничений;

5) целевые функции в задачах имеют противоположный смысл: в первой – максимум, во второй – минимум.

Задачи линейного программирования, обладающие пятью указанными формальными признаками, называются симметричными. Одна из них называется основной, а другая – двойственной.

В линейном программировании кроме симметричных двойственных пар существуют не симметричные двойственные пары, которые имеют следующий вид:

основная задача

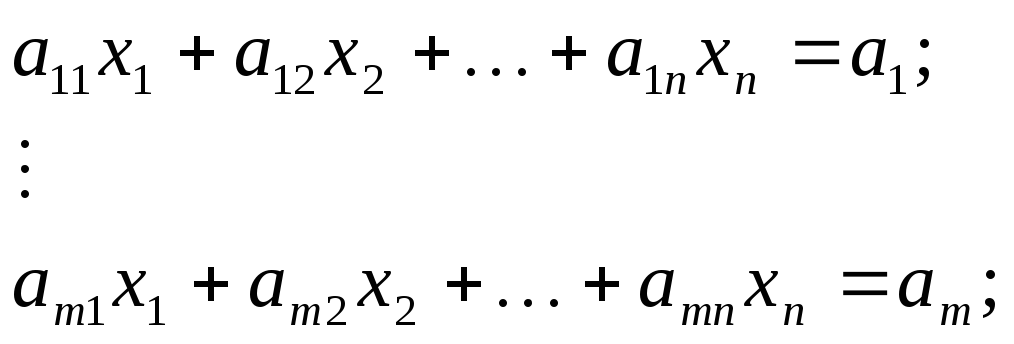(6.5)

; (6.6)

, ;

двойственная задача

(6.7)

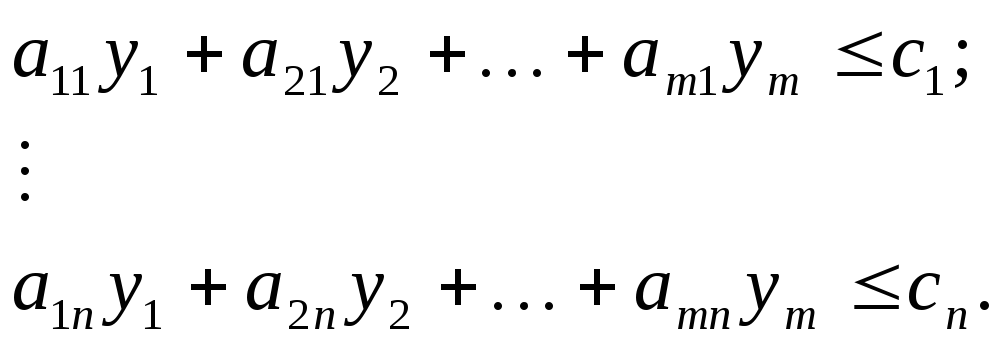(6.8)

Эти задачи отличаются от симметричной пары двумя особенностями:

1) ограничения задачи (6.5) – (6.6) выражены уравнениями вместо неравенств;

2) в задаче (6.7) – (6.8) отсутствуют условия не отрицательности переменных ,.

Общее правило построения двойственной пары.

К пяти признакам сформулированным ранее, необходимо добавить следующие:

1) в исходной ограничения неравенства следует записывать со знаком , если целевая функция стремится к минимуму, и со знаком, если целевая функция стремится к максимуму;

2) каждому ограничению неравенства исходной задачи соответствует в двойственной задаче условие не отрицательности переменных ;

3) каждому условию равенства соответствует переменная без ограничения на знак, и наоборот: не отрицательным переменным из основной задачи в двойственной задаче соответствуют ограничения неравенства, а неограниченным по знаку переменным соответствуют равенства.

Приведу теорему без доказательства, справедливую для любых двойственных задач.

Теорема. Если одна из двойственных задач имеет оптимальное решение, то и другая его имеет. Причём экстремальные значения целевых функций совпадают. Если же в одной задаче целевая функций не ограничена, то двойственная ей задача противоречива.