
- •4.12. Кривизна плоской кривой. Эволюта и эвольвента
- •4.13. Формула Тейлора7
- •Вопросы
- •4.14. Остаточный член формулы Тейлора в форме Лагранжа
- •4.15. Представление некоторых функций по формуле Тейлора
- •4.16. Приложения формулы Тейлора к исследованию функций
- •4.16.1. Главная часть бм
- •Вопросы
- •4.16.2 Возрастание и убывание функции
- •4.16.3. Экстремумы функции
- •4.16.4. Выпуклость и вогнутость кривой
- •4.16.5. Точки перегиба кривой
- •Вопросы
- •4.17. Формула Тейлора для числовой функции нескольких переменных
- •4.18. Локальные экстремумы функции нескольких переменных
- •4.19. Аппроксимация опытных данных по методу наименьших квадратов
- •4.20. Производная скалярного поля по направлению. Градиент
- •Вопросы
- •Задание для самостоятельного решения
- •4.21. Понятие о приближенных методах поиска локальных экстремумов
- •4.21.1. Релаксационный13 метод
- •4.21.2. Градиентный метод
- •4.21.3. Метод крутого восхождения (наискорейшего спуска)
- •4.21.4. Метод последовательного поворота симплекса
- •4.22. Условные экстремумы числовой функции нескольких переменных
- •4.23. Глобальные экстремумы числовой функции нескольких переменных
- •Задание для самостоятельного решения
- •4.24. Формулировка задачи линейного программирования
- •4.25. Понятие о задачах нелинейного и целочисленного программирования
- •4.26. Дифференциал и производная вектор-функции скалярного аргумента
- •Задание для самостоятельного решения
- •4.27. Кривизна пространственной кривой
- •Вопросы
- •Задание для самостоятельного решения
4.19. Аппроксимация опытных данных по методу наименьших квадратов
Отыскание локальных экстремумов функции нескольких перемен-ных используется при выравнивании опытных данных методом наименьших квадратов (МНК).
Задача выравнивания опытных данных ставится следующим образом.
Пусть для изучения связи двух величин х и у проведено п опытов, в результате которых получено п точек:
![]() .
.
По этим данным требуется построить в аналитической форме функцию
![]()
Е сли
бы опытные данные были абсолютно точными,
то кривая
должна была бы пройти через все
экспериментально полученные точки.
Однако в практических задачах такой
случай реализуется очень редко, и
величины
сли
бы опытные данные были абсолютно точными,
то кривая
должна была бы пройти через все
экспериментально полученные точки.
Однако в практических задачах такой
случай реализуется очень редко, и
величины
![]() обычно имеют существенные случайные
погрешности (см. рисунок). Возникает
задача о способе подбора функции
обычно имеют существенные случайные
погрешности (см. рисунок). Возникает
задача о способе подбора функции
По МНК эта задача решается следующим образом. Сначала определяется вид искомой функции, т.е. задается семейство функций
![]() (4.19.1)
(4.19.1)
зависящее от
параметров
![]() .
Это может быть, например, линейная
функция
.
Это может быть, например, линейная
функция
![]() квадратный трехчлен
квадратный трехчлен
![]() показательная функция
показательная функция
![]() и т.д. Выбор выражения (4.19.1) диктуется
либо теоретическими соображениями (при
этом могут использоваться физические
закономерности), либо характером
расположения экспериментально полученных
точек (здесь мы имеем дело с эвристическим
принятием решения). Сейчас мы не будем
заниматься проверкой правильности
выбора семейства (4.19.1) (это делается с
помощью методов теории вероятностей).
Отметим только, что этот выбор часто
бывает неоднозначным.
и т.д. Выбор выражения (4.19.1) диктуется
либо теоретическими соображениями (при
этом могут использоваться физические
закономерности), либо характером
расположения экспериментально полученных
точек (здесь мы имеем дело с эвристическим
принятием решения). Сейчас мы не будем
заниматься проверкой правильности
выбора семейства (4.19.1) (это делается с
помощью методов теории вероятностей).
Отметим только, что этот выбор часто
бывает неоднозначным.
Далее вводятся в рассмотрение отклонения опытных данных от любой кривой семейства (4.19.1):
![]() (4.19.2)
(4.19.2)
Отклонение всей совокупности опытных точек от теоретической кривой (4.19.1), согласно МНК, оценивается как
![]() (4.19.3)
(4.19.3)
Тогда
естественно из семейства (4.19.1) отобрать
такую кривую, для которой отклонение
минимально. Так как
![]() изменить можно только за счёт вариации
параметров
,
то, используя необходимые условия
экстремума, получим
изменить можно только за счёт вариации
параметров
,
то, используя необходимые условия
экстремума, получим
![]()
или в развернутом виде (см. (4.19.3))
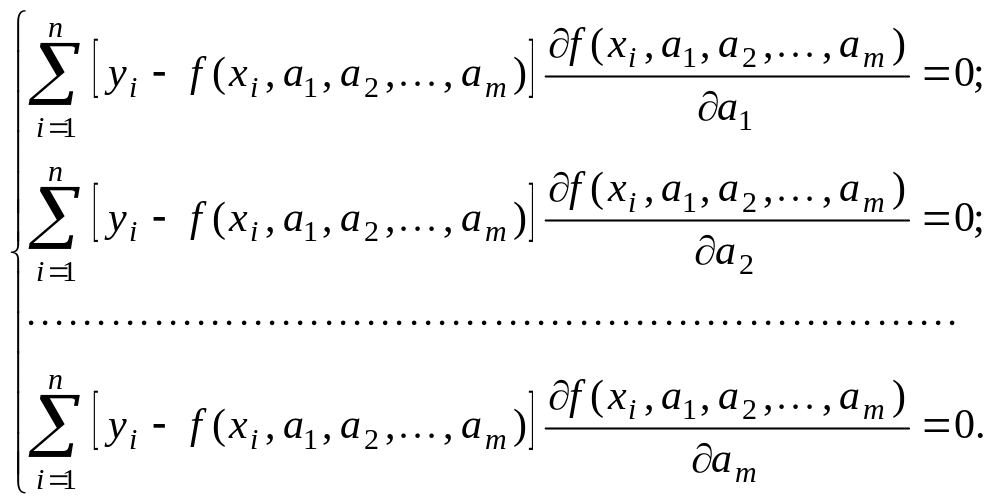 (4.19.4)
(4.19.4)
Решая систему (4.19.4), можно найти стационарные точки функции (4.19.3). Обычно таких точек бывает ровно одна, она является точкой минимума и соответствует такой кривой семейства (4.19.1), для которой отклонение от совокупности опытных данных будет наименьшим.
П р и м е р
Подобрать линейную зависимость электрического сопротивления молибдена от температуры , используя следующие опытные данные
|
1178 |
1489 |
1988 |
2289 |
|
28.94 |
37.72 |
52.70 |
61.97 |
Для решения используем линейную функцию = aT+b (в физике такая зависимость известна). Составим систему (4.19.4) для данного случая:

Отсюда получаем

С помощью измеренных значений и находим
![]() ;
;
![]()
Окончательно записываем систему уравнений для вычисления a и b:
![]()
решая которую получаем a = 0,032, b = – 6,9, т.е. искомая зависимость такова:
= 0,032T – 6,9.
