Вполне понятно, что точная верхняя грань будет достигаться при безграничном измельчении делений (каждая вновь вводимая точка может только увеличивать сумму в (4.11.1)). Если п конечно, то дуга называется спрямляемой.

П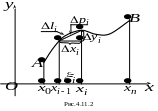 редположим, что дуга АВ задана уравнением y = f (x) (рис. 4.11.2). Произведя разбиение дуги на п частей, для i-того деления будем иметь

По формуле Лагранжа

,

поэтому

; .

Пусть Тогда

(4.11.2)

где – наибольшее значение модуля производной на рассматриваемом отрезке.

Легко видеть, что точная верхняя грань обладает следующим свойством:

(доказательство осуществляется от противного – сделать самостоятельно). Поэтому на основании (4.11.1), (4.11.2) имеем

. (4.11.3)

По аналогии с (4.11.2):

где – наименьшее значение модуля производной на отрезке

Отсюда (4.11.4)

Из неравенств (4.11.3), (4.11.4) следует, что

.

Пусть теперь , тогда естественно обозначить через , а l – через :

.

При в силу непрерывности производной имеем , т.е. в силу первого признака существования предела

или (4.11.5)

Формула (4.11.5) выражает дифференциал длины дуги плоской кривой. Если кривая задана параметрически

то ,

т.е.

(предполагается, что

Достаточным условием существования дифференциала длины дуги (4.11.5) является Аналогично при параметрическом задании кривой достаточное условие существования дифференциала состоит в том, что

Как известно из школьного курса математики, всякая величина может быть вычислена по её дифференциалу с помощью интегрирования. Этот вопрос будет рассмотрен позднее.

4.12. Кривизна плоской кривой. Эволюта и эвольвента

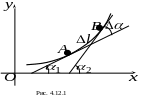
Рассмотрим вопрос о том, как быстро изменяется на­правление касательной к кривой. Для этой цели введём так называемый угол смежности (рис. 4.12.1). Тогда среднюю скорость поворота касатель­ной при перемещении точки из положения А в положение В можно определить как

(4.12.1)

Вопрос

Подумайте, почему не рассматривают отношение

Выражение (4.12.1) называют средней кривизной кривой на

Величина

(4.12.2)

называется кривизной кривой в соответствующей точке.

Для окружности т.е.

Если кривая задана уравнением то вывод формулы для вычисления кривизны выполняется следующим образом:

;  ;

 ;

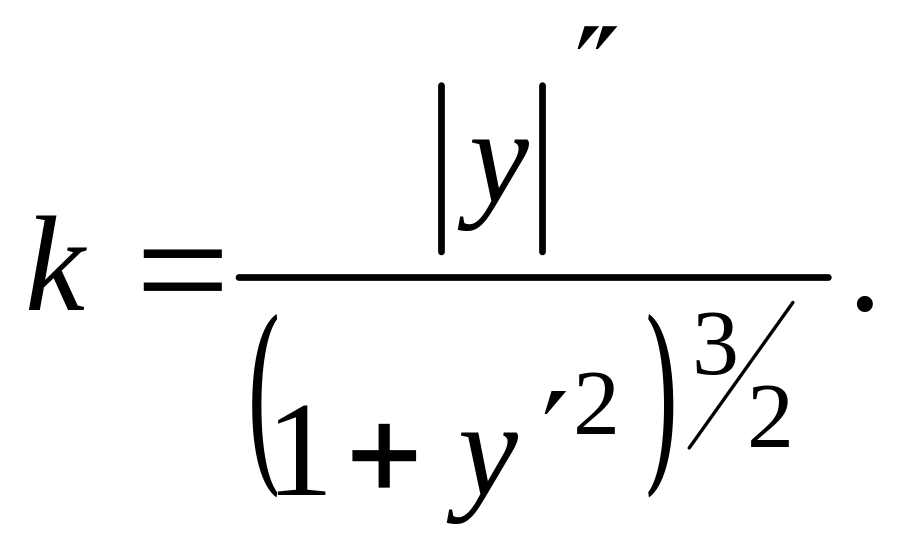(4.12.3)

Величина

(4.12.4)

называется радиусом кривизны кривой в соответствующей точке. Очевидно, что

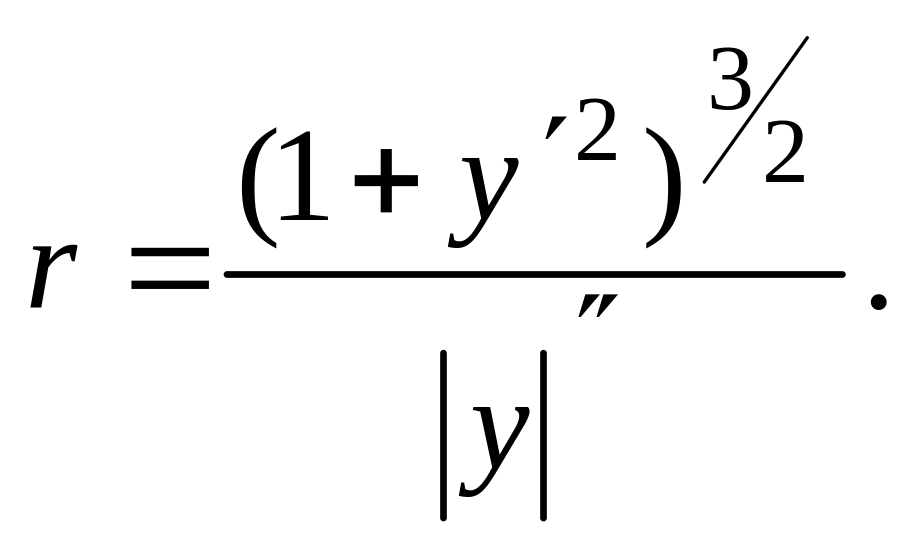
Интересно отметить, что в точке экстремума

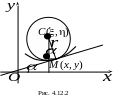В связи с изложенным естественно возникает мысль о замене кривой вблизи рассматриваемой точки дугой окружности. Это приводит к понятию круга кривизны ¹, который (рис. 4.12.2)

1. касается кривой в рассматриваемой точке;

2. имеет ту же кривизну, что и кривая в рассматриваемой точке;

3. лежит по ту же сторону от касательной к кривой, что и сама кривая вблизи рассматриваемой точки.

Центр круга кривизны называется центром кривизны кривой в рассматриваемой точке. Вычислим координаты круга кривизны, воспользовавшись рис. 4.12.2:

(4.12.5)

Выразим через производные функции y = f (x):

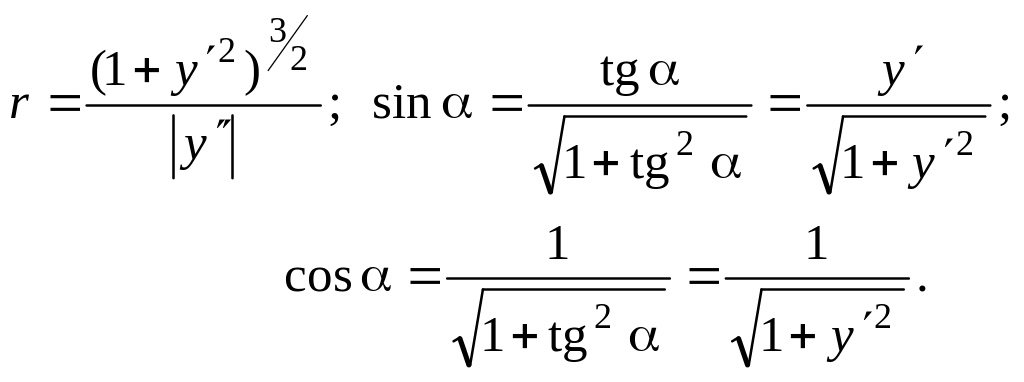
Отсюда с помощью (4.12.5) имеем

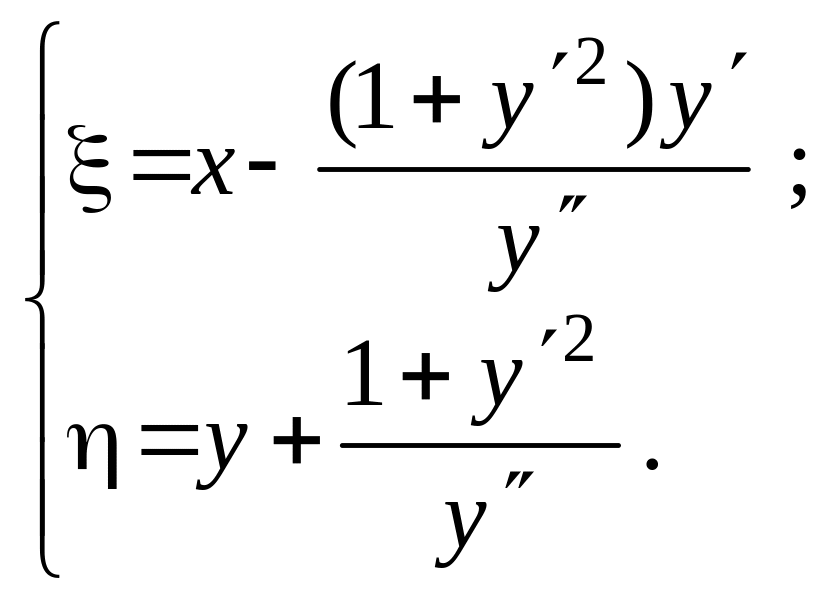(4.12.6)

Знак модуля производной у" опущен, так как y" > 0 на рис.4.12.2. Если

y''< 0, то r придется откладывать на нормали к кривой в точке М в противоположную сторону, т.е. формулы (4.12.6) справедливы и для этого случая.

В формулах (4.12.6) величины у, у' и у" должны быть заменены на f (x), и (соответственно). Поэтому ясно, что их можно рассматривать как параметрические уравнения некоторой кривой с параметром х. 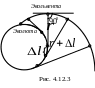Эта кривая называется эволютой⁵. Точнее, эволютой следует назвать множество всех центров кривизны данной кривой. Например, для окружности эволюта состоит лишь из одной точки — центра этой окружности. Кривая линия по отношению к своей эволюте называется эвольвентой⁶ .

Пара кривых эволюта-эвольвента обладают двумя очень интересными свойствами (их доказательства мы не приводим):

1) нормаль к эвольвенте является касательной к эволюте;

2) приращение длины дуги эволюты равно приращению радиуса кривизны эвольвенты.

Для иллюстрации указанных свойств на рис. 4.12.3 показана эвольвента окружности. Можно себе представить, что с катушки в форме эволюты разматывается нерастяжимая гибкая нить; тогда траектория фиксированной точки на этой нити совпадает с эвольвентой. Если катушку взять некруглой, то получится эвольвента более сложной формы).

П р и м е р

Найти уравнение эволюты параболы у²= 2рх.

Решение находим с помощью (4.12.6):

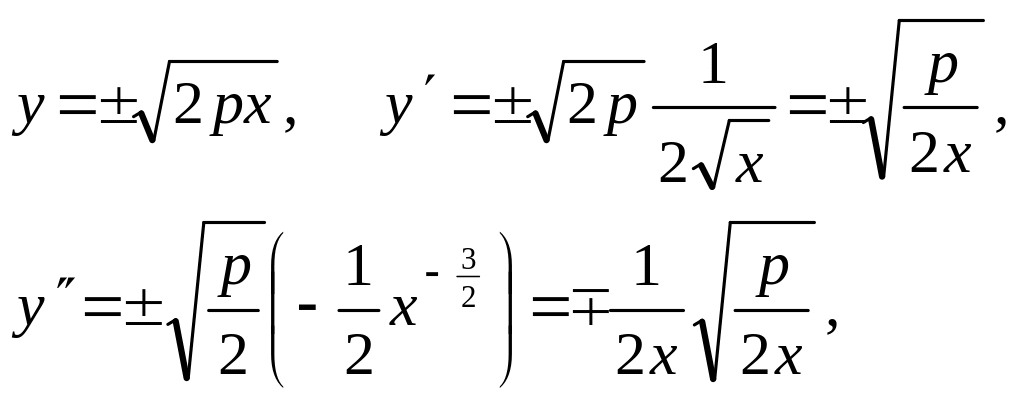
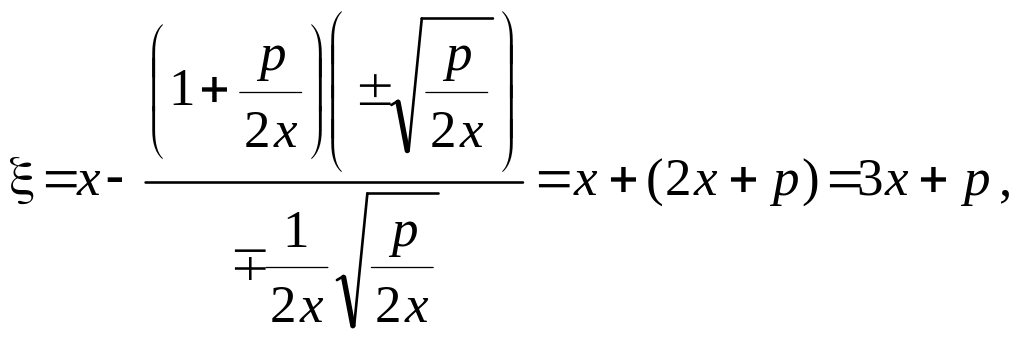
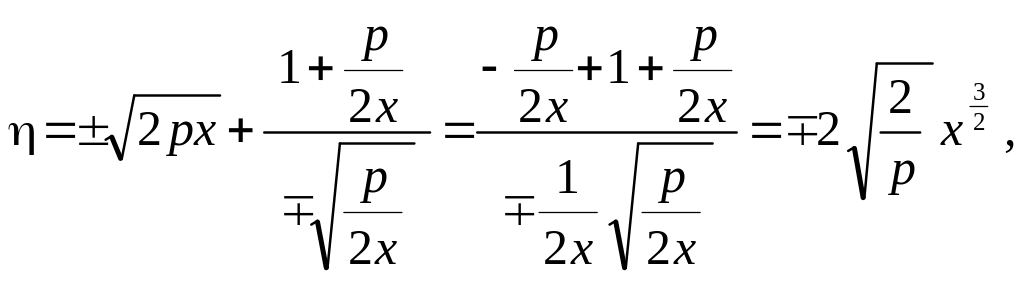
откуда , (рис. 4.12.4).

З адание для самостоятельного решения

1. Вычислить кривизну (в произвольной точке):

а) эллипса x = аcost, y = bsint ; б) гиперболы ху = 1;

в) параболы четвертого порядка у = ах⁴.

2. Найти эволюты:

а) эллипса x =cost, y = bsint; б) гиперболы ху =1.