
- •Глава первая элементы теории множеств
- •1.1.1.Множество и подмножество
- •Вопросы
- •1.1.2. Объединение и пересечение множеств
- •Вопросы
- •1.1.3. Разность множеств. Дополнение множества
- •Вопросы
- •1.1.4. Декартово произведение множеств
- •Вопросы
- •1.1.5. Мощность множества
- •Вопросы
- •Глава вторая линейная алгебра и аналитическая геометрия
- •2.1. Понятие о матрице
- •2.2. Определители второго и третьего порядков
- •2.3. Основные свойства определителей
- •2.4. Минор и алгебраическое дополнение
- •Задание для самостоятельного решения
- •2.5. Понятие об определителе любого порядка
2.4. Минор и алгебраическое дополнение
Рассмотрим определитель n-ного порядка.
Минором
![]() элемента
элемента
![]() определителя n-ного
порядка
называется определитель (n
– 1)-ного порядка, который получается
из
вычеркиванием i-той
строки и k-того
столбца.
определителя n-ного
порядка
называется определитель (n
– 1)-ного порядка, который получается
из
вычеркиванием i-той
строки и k-того
столбца.
Алгебраическим дополнением
![]() элемента
элемента
![]() называется его минор
называется его минор
![]() ,
умноженный на
,
умноженный на
![]() :
:
![]() .
.
Например, минор для элемента
![]() в определителе
в определителе

будет иметь вид
![]() ,
,
а алгебраическое дополнение равно
![]() .
.
Нетрудно видеть, что знаки, которые следует ставить перед соответствующими минорами при вычислении алгебраических дополнений, чередуются в шахматном порядке:
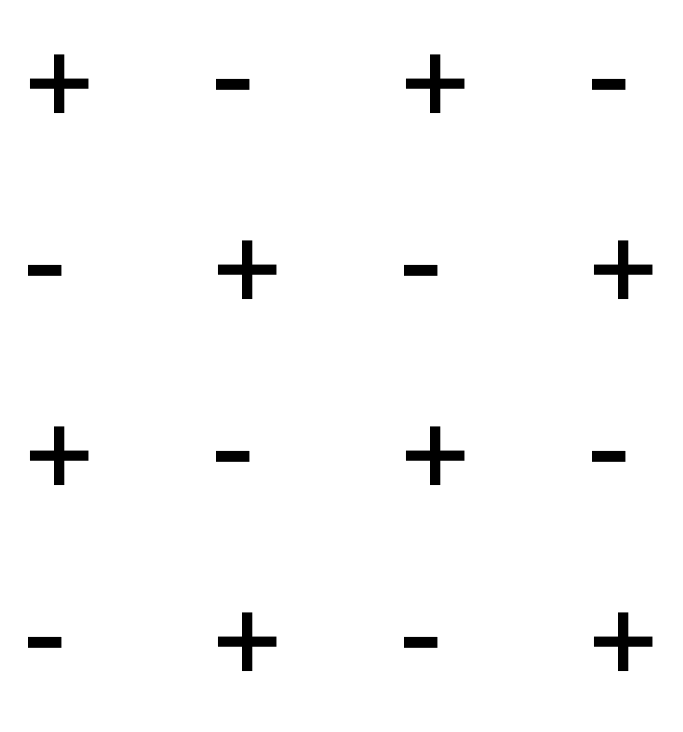
В качестве упражнения выпишите
алгебраические дополнения для элементов
![]() в определителе
в определителе
 .
.
Если рассматривается прямоугольная матрица, то понятие минора вводится по-иному.
Выберем в
![]() матрице какие-либо k
строк и k столбцов
матрице какие-либо k
строк и k столбцов
![]() Из элементов, стоящих на пересечении
выделенных строк и столбцов, составим
определитель k-того
порядка. Любой из таких определителей
называется минором k-того
порядка для данной матрицы.
Из элементов, стоящих на пересечении
выделенных строк и столбцов, составим
определитель k-того
порядка. Любой из таких определителей
называется минором k-того
порядка для данной матрицы.
Например, для матрицы
![]()
можно образовать миноры третьего, второго и первого порядков (определитель первого порядка считается равным своему элементу). Вот некоторые из них:
,![]() ,
,![]() .
.
Задание для самостоятельного решения
1. Сколько миноров k-того порядка можно составить для матрицы?
2. Сколько всего различных миноров может иметь матрица?
3. Выпишите все миноры для матрицы
![]() .
.
2.5. Понятие об определителе любого порядка
Рассмотрим особенности формулы, выражающей величину определителя третьего порядка:

Очевидно, что
1) в правой части слагаемыми являются произведения элементов определителя, взятых по одному из каждой его строки и каждого столбца;
2) половина из этих произведений взята со знаком «плюс», другая — со знаком «минус».
Если расположить элементы в произведениях так, как это сделано в формуле (2.5.1) — в порядке возрастания первых индексов (номеров строк), то нетрудно обнаружить закономерность образования знаков для слагаемых в формуле (2.5.1). Будем говорить, что числа i, j образуют инверсию, если i > j
1
В некоторых руководствах запись
исключает случай
![]() и использует запись
и использует запись
![]() ,
когда возможно равенство
.
,
когда возможно равенство
.
2 Леонард Эйлер (1707—1783) — великий математик, физик и астроном, член Петербургской и Берлинской академий наук. Родился в Швейцарии, жил и работал в России с 1727—1741 г., и с 1766 по 1783 г.
Дж. Венн (1834—1923) — английский логик.
3 idem — одно и то же (лат).
4 А. де Морган (1806—1871) — английский математик.
5 Дж. Буль (1815—1864) — английский математик, основоположник математической логики.
6 continuum — непрерывный, сплошной (лат.).
7 Георг Кантор (1845—1918) — немецкий математик, разработал основы теории мно-
жеств.
8 Л. Кронекер (1823—1891) — немецкий математик.
9 determinans — определяющий (лат.).
