Вопросы

1. Как проиллюстрировать равенство (1.2.5) с помощью диаграммы Эйлера-Венна?

2. Чему равно , , , ?

3. В каких отношениях находятся множества , 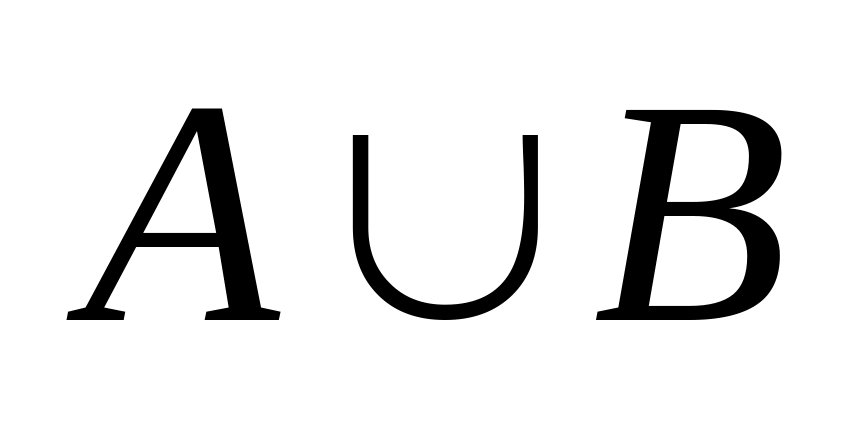, ? Решение проиллюстрируйте с помощью диаграмм Эйлера-Венна.

1.1.3. Разность множеств. Дополнение множества

Разностью множеств и называется множество, состоящее из всех тех элементов множества , которые не принадлежат множеству .

О

бозначается разность , ее геометрическая иллюстрация приведена на рис. 1.3, а.

a б

Рис.1.3

В этом определении существенен порядок, в котором следуют множества:

.

Например, , , .

Разность называется дополнением множества до множества ( — основное множество, ). Дополнение обозначается через (или ). Его геометрический смысл ясен из рис. 1.3, б.

Вопросы

1. Чему равно , , , , , , , ?

2. Как выразить через дополнения , ?

Полученные в соответствии с последним вопросом равенства называются формулами де Моргана.⁴ Для произвольного числа множеств они имеют вид

, . (1.3.1)

Множество элементов , , ... , в котором определены операции , , и заданы два особых элемента и , называется алгеброй Буля⁵ (предполагается, что при этом выполняются все соответствующие свойства действий над множествами).

1.1.4. Декартово произведение множеств

Любым двум объектам и можно сопоставить их упорядоченную пару . Этот прием лежит в основе определения декартова произведения множеств.

Декартовым произведением множеств А и В называется множество всех упорядоченных пар элементов , в которых , .

Обозначается декартово произведение через . Его геометрическая интерпретация приведена на рис. 1.4, где показаны следующие множества:

;

.

Декартово произведение n множеств определяется аналогично:

Напомним обозначения:

, , ... , .

Вопросы

При каком условии:

а) ,

б) ?

1.1.5. Мощность множества

Понятие мощности множества связано с запасом элементов в этом множестве.

Два множества имеют (по определению) одинаковую мощность, если между их элементами можно установить взаимно однозначное соответствие. Такие множества называются эквивалентными (равномощными).

Два конечных множества эквивалентны тогда и только тогда, когда они состоят из одинакового числа элементов.

Приведем примеры эквивалентных бесконечных множеств:

1) множество натуральных чисел эквивалентно своему подмножеству , в которое входят все четные положительные числа, так как

2) в прямоугольном треугольнике множество точек гипотенузы эквивалентно множеству точек любого катета (рис. 1.5,а);

3) множества точек на двух любых окружностях являются эквивалентными (рис. 1.5,б).

Множество, эквивалентное множеству натуральных чисел, называется счетным.

Рис.1.5

Приведем примеры счетных множеств:

; ; , .

Теорема 1. Объединение конечного или счетного множества счетных множеств является счетным множеством.

Для доказательства рассмотрим счетную совокупность непересекающихся счетных множеств, т. е.

, (1.5.1)

где

;

…………………………….

Тогда объединение будет состоять из элементов, которые можно выписать в одну строку (и, следовательно, пронумеровать), «снимая» элементы послойно, как показано стрелками на схеме:

(1.5.2)

При этом никакие элементы упущены не будут, и теорема при условии (1.5.1) доказана.

Если некоторые из множеств имеют непустые пересечения друг с другом или рассматривается конечная совокупность множеств то доказательство изменяется несущественно: в строке (1.5.2) некоторые элементы нужно исключить, а оставшиеся элементы образуют счетное множество (можно, например, оставить все элементы множества ). Таким образом, теорема 1 доказана полностью.

Теорема 2. Множество рациональных чисел является счетным множеством.

Для доказательства введем счетные множества

; ; ; ... .

Очевидно, что множество

,

есть множество положительных рациональных чисел. Согласно теореме 1 оно является счетным. Точно так же счетным будет и множество — отрицательных рациональных чисел. Множество всех рациональных чисел

тоже оказывается счетным множеством в силу теоремы 1, что и требовалось доказать.

Теорема 3. Множество действительных чисел на отрезке [0, 1] имеет мощность, большую мощности счетного множества.

Для доказательства теоремы наряду с множеством

рассмотрим множество десятичных дробей

, .

Среди элементов множества есть конечные и бесконечные десятичные дроби. Заметим, что каждую конечную десятичную дробь можно представить в виде бесконечной с периодом 9, например, 0,4=0,3999... =0,3(9). Условимся считать, что в множество В входят лишь все бесконечные десятичные дроби. При выполнении этого условия нетрудно проверить, что

1. между множествами и можно установить взаимно однозначное соответствие, т. е. и — эквивалентные множества;

2. если две дроби из различаются хотя бы одним десятичным знаком, то эти дроби выражают различные действительные числа.

При этом множество оказывается несчетным. Это доказывается от противного.

Предположим, что множество счетное, т. е.

.

Образуем новую бесконечную десятичную дробь

,

выбрав

, , , ... . (1.5.3)

Очевидно, что, с одной стороны, , т. е. . С другой стороны, в силу (1.5.3) . Полученное противоречие убеждает нас в том, что множество счетным быть не может. Поскольку оно содержит в себе счетное множество, его мощность следует считать большей мощности счетного множества.

Всякое множество, эквивалентное множеству действительных чисел отрезка [0, 1], имеет (по определению) мощность континуума.⁶