Глава первая элементы теории множеств

1.1.1.Множество и подмножество

Понятие множества является одним из первичных, неопределяемых математических понятий. Синонимами термина «множество» являются «совокупность», «собрание» некоторых объектов (элементов).

Например, можно говорить о множестве натуральных чисел, о множе­стве сторон многоугольника, о множестве точек на данной прямой и т.д.

Множества обычно обозначают прописными латинскими буквами, а их элементы — малыми. Запись фиксирует тот факт, что является элементом множества . Формула означает, что не является элементом множества (допускается также запись ).

Напомним известные из школьного курса математики обозначения следующих множеств:

— множество действительных (вещественных) чисел; — множество натуральных чисел; — множество целых чисел; — множество рациональных чисел.

Если множество содержит несколько («конечное число») элементов, то его называют конечным. В противном случае множество называется бесконечным.

Например, множества

, ,

являются конечными, а множества

,

будут бесконечными (символ : в формулах следует читать «такие, что»; иногда вместо : пишут /).

Множество, не содержащее ни одного элемента, называется пустым. Пустое множество обозначают через .

Если каждый элемент множества является элементом множества , то называют подмножеством множества . Обозначается это так: или . Понятие подмножеств на плоскости проиллюстрировано на рис.1.

Х

Y

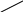
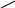
Рис.1.1

Например, .

Отношение между множествами не исключает возможности совпадения и .¹

Более того,

(1.1.1)

Символ означает равносильность высказываний, записанных слева и справа от него (символ эквивалентности).

Считается, что (для любого множества ).

Если в какой-нибудь задаче рассматриваются подмножества одного и того же множества , то называют основным (или универсальным, или фундаментальным, или единичным) множеством.

Например, при рассмотрении множеств типа отрезок (замкнутый промежуток) или интервал (открытый промежуток):

,

основным будет множество .

Вопросы

1. Образовать все подмножества множества {1, 2, 3}.

2. Как выражается количество различных подмножеств множества, состоящего из 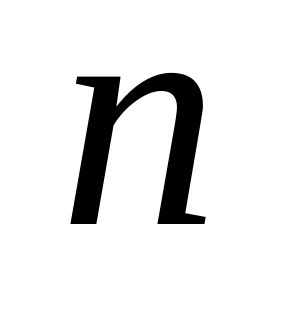элементов?

3. Пояснить с помощью графика, из каких элементов состоит множество .

1.1.2. Объединение и пересечение множеств

Объединением (суммой) множеств и называется множество, образованное из всех тех элементов, которые входят хотя бы в одно из множеств или .

a)

б)

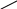
A

B

А

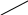
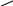
A B A B

Рис.1.2

Объединение множеств обозначается через ; геометрическая иллюстрация этого понятия дана на рис. 1.2,а.

Подобные геометрические интерпретации называются диаграммами Эйлера-Венна.²

Аналогично определяется объединение множеств

или или .

Например,

1. , , ;

2. , ,

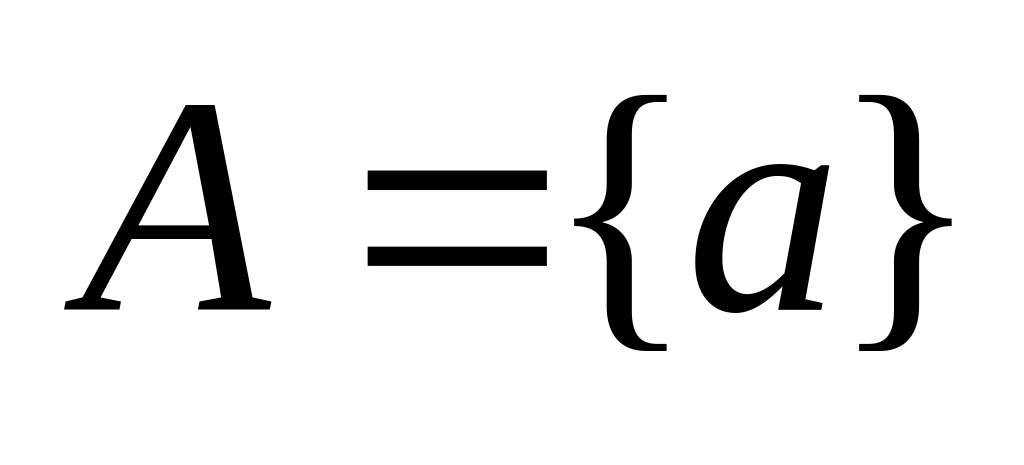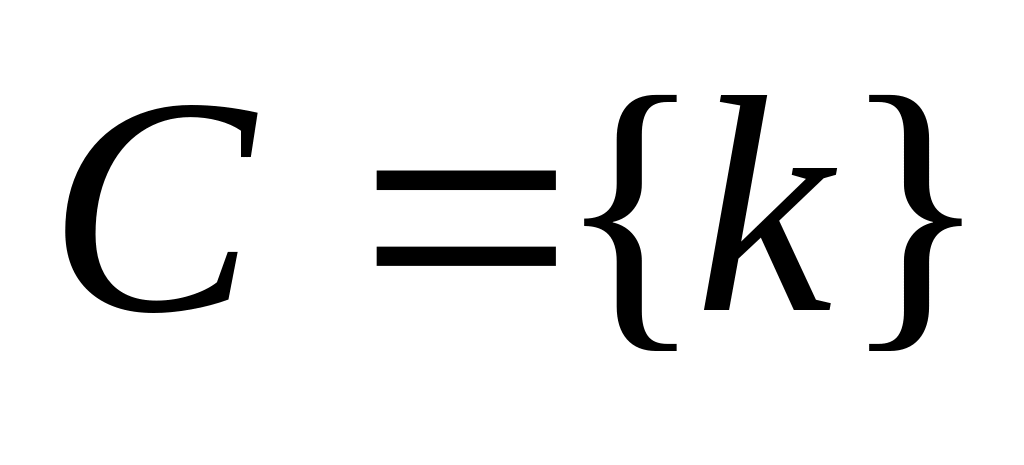
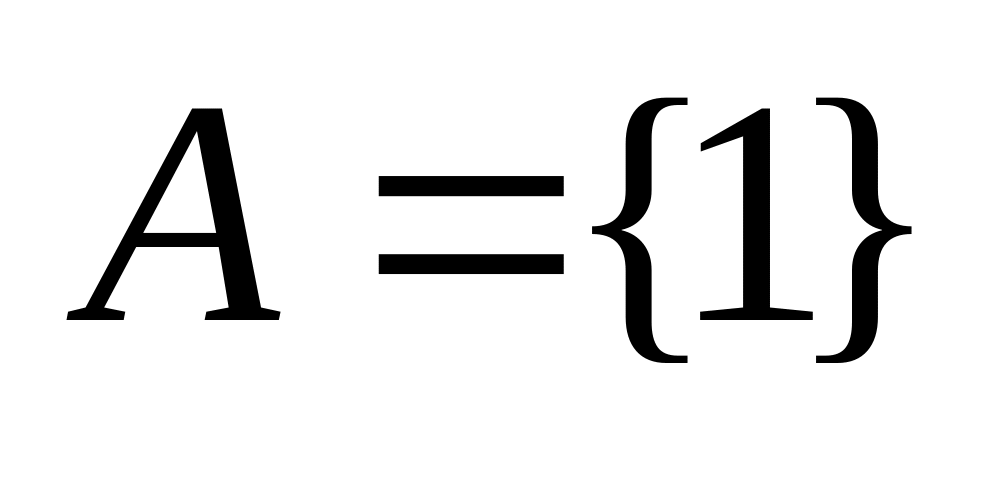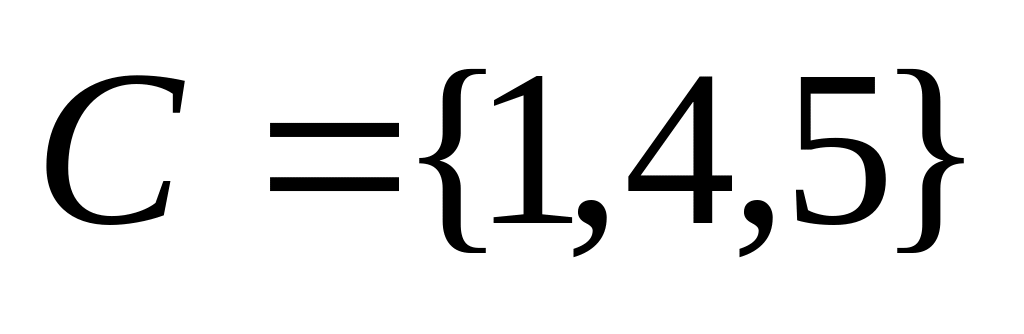
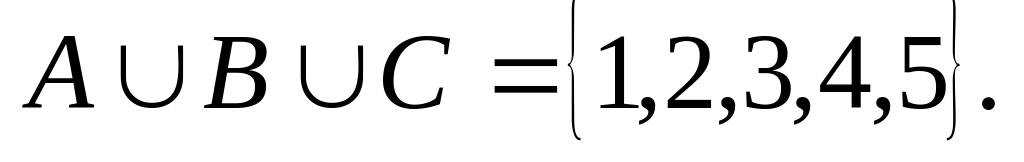
Символ импликации соответствует словам «влечет», «следует», «если ... , то ...».

Пересечением (произведением) множеств и называется множество, образованное из всех тех элементов, которые принадлежат и множеству , и множеству .

Обозначается пересечение через , геометрическая иллюстрация приведена на рис. 1.2, б. Чтобы не путать знаки и , рекомендуется первый рассматривать как трансформированную букву (от «Union» — союз), а второй — как трансформированную букву П («пи»), которой означают произведение.

Аналогично определяется пересечение множеств

Например,

1. , , ;

2. , , .

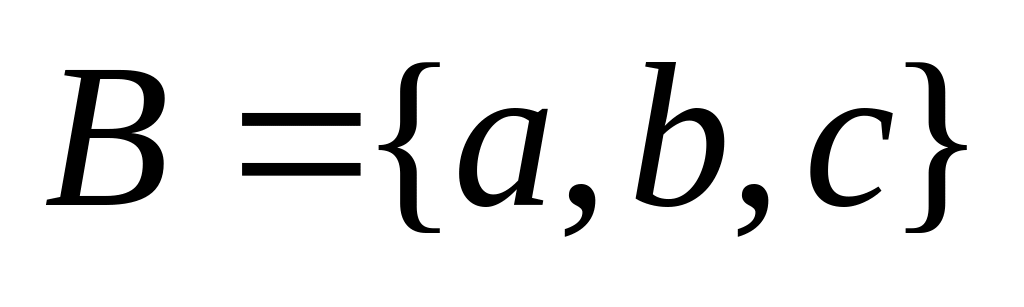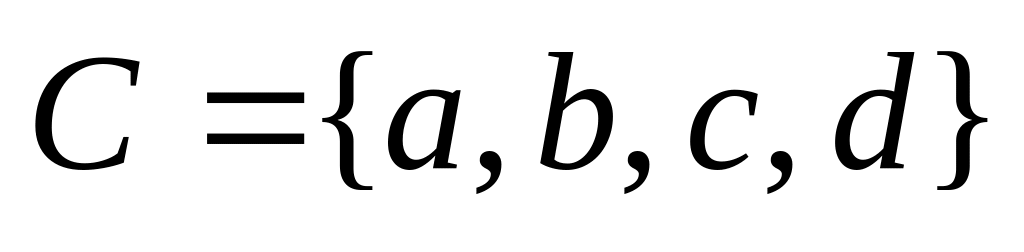
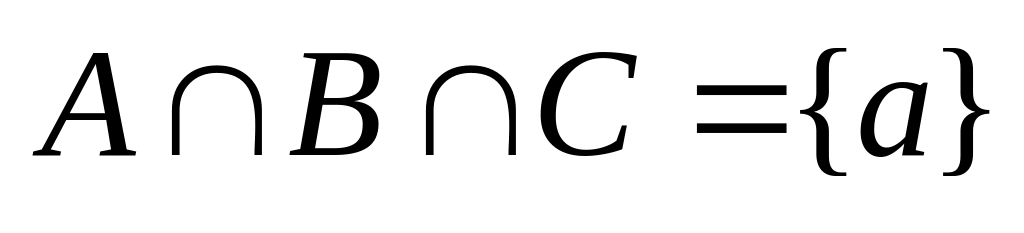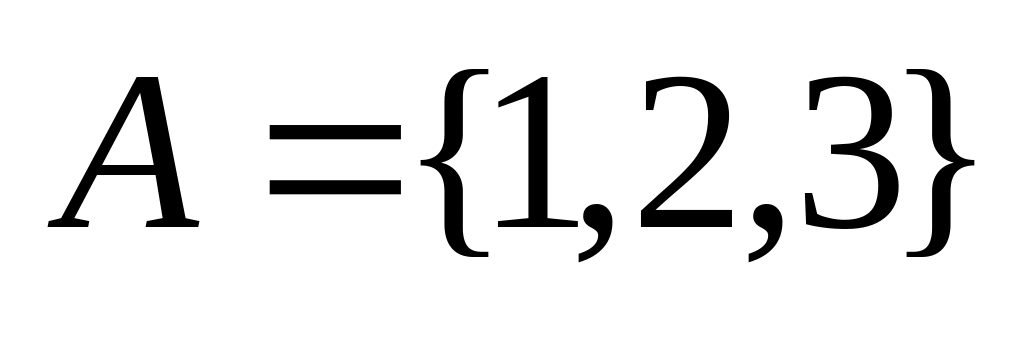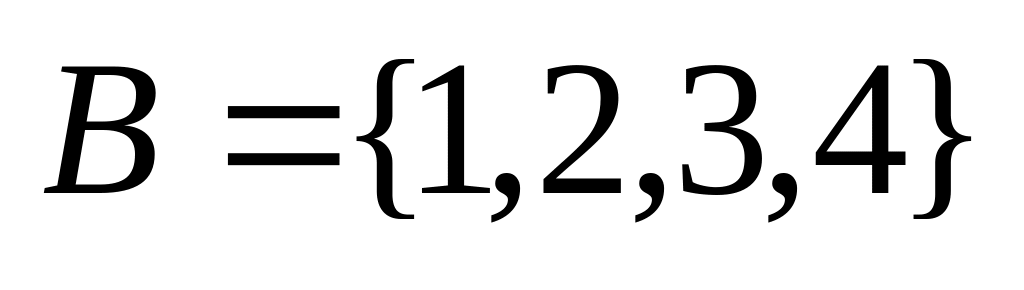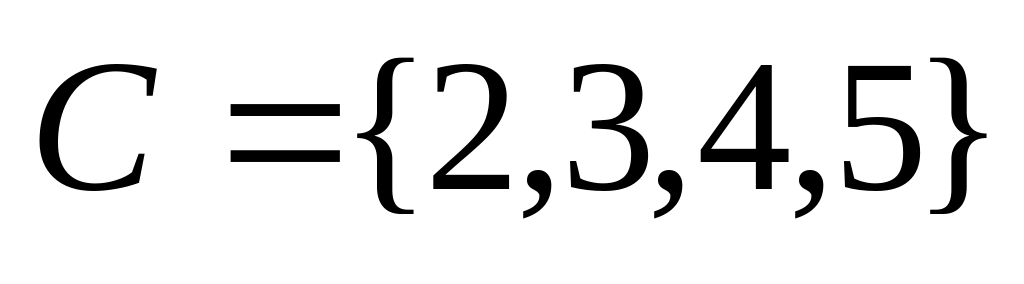
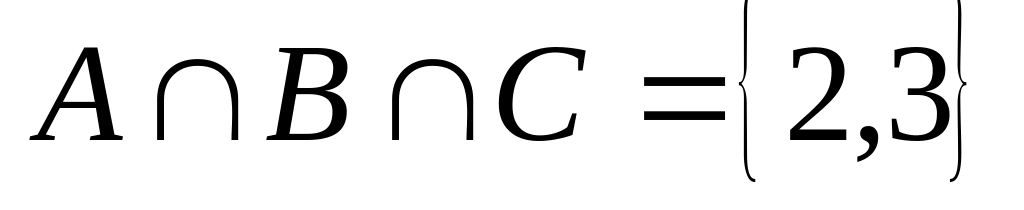Относительно введенных действий над множествами справедливы следующие свойства:

1. коммутативность (переместительный закон): 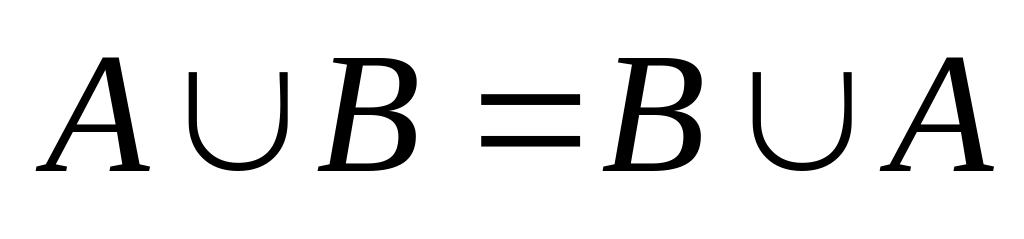, 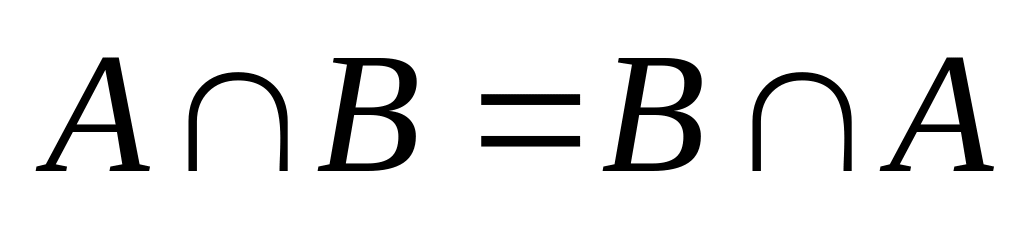; (1.2.1)

2. ассоциативность (сочетательный закон): , 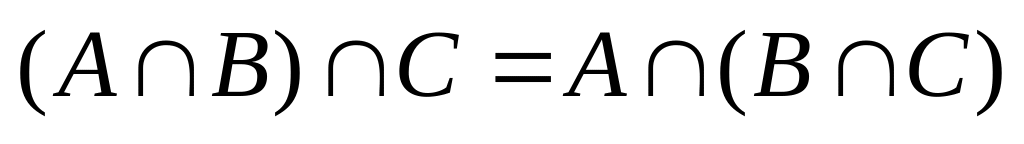; (1.2.2)

3. идемпотентность³ (тождественность): , ; (1.2.3)

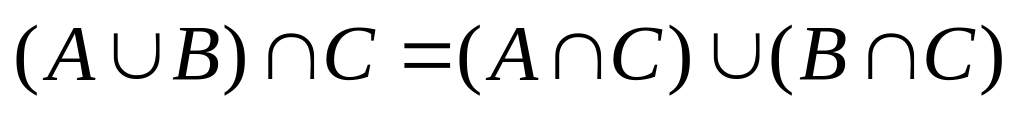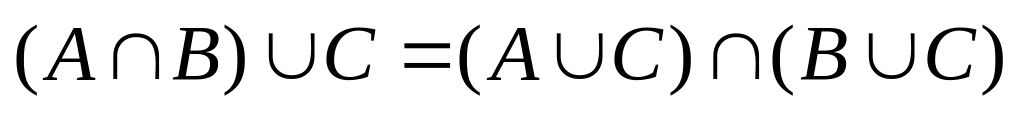4. дистрибутивность (распределительный закон): , (1.2.4) . (1.2.5)

В алгебре множеств для доказательства равенства вида = ( — левая часть равенства, — его правая часть) необходимо и достаточно в соответствии с (1.1.1) установить, что и . В качестве примера приведем схему доказательства равенства (1.2.5)

, (1.2.6)

откуда следует, что (заметим, что случаи 1) и 2) в (1.2.6) не исключают друг друга).

Если в (1.2.6) повернуть знаки импликации в противоположную строну, то получаются снова верные соотношения, из которых следует, что (проверить самостоятельно).