Лекция 5

Построение кристаллической решётки Вигнера-Зейтца.

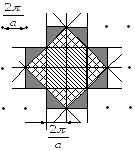
Примитивная кристаллическая решётка в пл-ти.

- 1 зона Бриллюэна

- 2 зона Бриллюэна

- 3 зона Бриллюэна

Примитивная ячейка Вигнера-Зейтца строится так, чтобы каждый узел решётки находился в центре области, точки которой лежат ближе всего к этому центру, чем к какой-либо другой точке решётки. Если подвергнуть эту ячейку трансляции, то она заполнит всё пространство кристалла без перекрытия.

Правила построения:

1. Проводим линии перпендикулярные отрезкам, соединяющих исходную точку с ближайшими соседними точками;

2. выбираем наименьший многогранник, ограниченный плоскостями, перпендикулярными связям, содержащий исходную точку.

Обратная решётка.

Каждой реальной прямой решётке сложно сопоставить решетку, построенную в обратном пространстве, т.е. в пространстве. В котором радиус-вектор определяется так, что его модуль

, где- некоторая величинапериоду решётки.

Значение связано с длиной волны Дебройля для.

Вектор трансляции такой решётки определяется аналогично вектору трансляции в обычной решётке.

;;

Связь объёма в обратной решётке с объёмом в прямой решётке:

Рассчитаем произведение векторов:

Векторы иэквивалентные, т. е. существуют в обратной решётке такие области пространства где все векторасоответствуют векторам. Неэквивалентны они только в первой зоне Бриллюэна.

Зона Бриллюэна номера Nобратной решётке представляет собой замкнутый многогранник, ограничивающий с внешней стороны плоскостями, проходящими через середины векторов, проведённых во все узлы обратной решётки с номеромNиз начала координат- пространства, а с внутренней стороны – плоскостями зоны с номеромN-1. Объёмы всех зон Бриллюэна одинаковы и равны объёму первой зоны Бриллюэна.

Индексы узлов направлений и плоскостей кристаллической решётки.

Индексы узлов кристаллической решётки определяются координатами каждого узла, выраженные через параметры решётки.

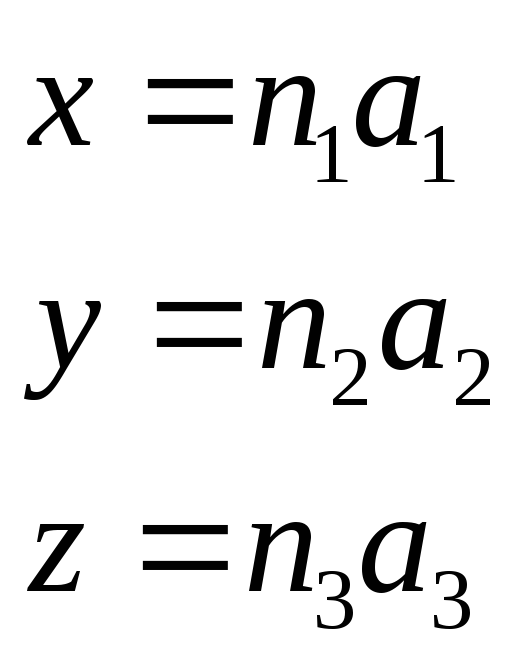
- индексы узлов.

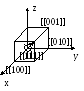
Для описания в кристаллической решётке выбирается прямая, проходящая через начало координат и её направление описывается индексами первого узла, через который он проходит:

Индексы плоскостей (индексы Миллера ) обратнопропорциональны отрезкам, отсекаемым плоскостью на осях координат, выраженных через периоды решётки.

Правило определения индексов плоскостей:

1. находим точки в которых данная плоскость пересекает основные координатные оси и записываем их значение через периоды решётки;

2. берём обратные значения полученных чисел и приводим их к общему знаменателю.

Полученные значения в числителе являются индексами Миллера. Индексы Миллера обозначают не одну плоскость, а совокупность параллельных плоскостей.

Реальная кристаллическая структура вещества. Дефекты кристаллической решётки.

Реальные кристаллические материалы в отличие от идеальных монокристаллов представляют собой чаще всего «мозаичную структуру», т. е. состоящих из отдельных групп атомов, которые отделены друг от друга межкристаллической структурой. По этой границе локализуется множество дефектов. Дефекты можно разделить на:

1. нуль-мерные (точечные дефекты);

2. одномерные (линейные дефекты);

3. дву-мерные (пространственные).

1. Точечные статические дефекты:

А) дефекты Френкеля

Атомы из-за теплового движения покидают узлы .

Дефекты Шотки

Частица покидает кристаллическую ршётку.

Б) примесные дефекты, возникают в результате внедрения примесей в основное вещество.

В результате возникают внедрения и замещения.

2. Точечные динамические дефекты.

а) электронные дефекты обусловлены появлением электронов и дырок.

б) временное искажение регулярной кристаллической решётки в результате поглощения энергии, т. е. появлением дополнительных ________.

3. Линейные деформации.

Если точечные деформации приводят к нарушению регулярности кристаллической структуры в окрестности одного или двух узлов, то это приводит к линейному нарушению кристаллической решётки.

Они могут быть краевыми (возникают при деформации сдвига) и винтовые (возникают при повороте одних слоёв относительно других).

4. Двумерные деформации.

К ним относятся деформации на границах между _________ (монокристаллами и самой кристаллической решёткой).

Динамика кристаллической решётки. Движение медленной подсистемы.

Как известно ионы, атомы и молекулы, находящиеся в узлах кристаллической решётки совершают колебания около положения равновесия из-за теплового движения.

Потенциальная энергия в положении равновесия является минимальной. Совершая тепловое движение частицы взаимодействуют между собой.

Рассмотрим одномерную цепочку составленную из одномерных атомов.

Пусть N-ый атом находится в точке С координат равной 0. Смещение данного атома .

Если бы смещался только один атом, то то сила действующая на него была бы пропорциональна смещению, т. к. N-ый атом взаимодействует сN+1 иN-1 атомами, то сила взаимодействия:

Решение ищем в виде:

,

Где – координата атома

,

- период одномерной решётки;

- номер атома.

Т.к. первый и последний атомы закреплены, то решение представляет собой уравнение стоячей волны. Определим из граничных условий :

При

,

Подставим данное решение в исходное уравнение. После преобразования:

- дисперсионная зависимость.